

fpga在通信方面的应用_怎么用FPGA做算法
可编程逻辑
描述
fpga在通信方面的应用
现场可编程门陈列(FPGA)芯片在许多领域均有广泛的应用,特别是在无线通信领域里,由于具有极强的实时性和并行处理能力,使其对信号进行实时处理成为可能。本节不仅对FPGA技术在现有无线通信中的应用领域作了详细的分析,并对其在未来无线通信中的应用发展作了展望。
FPGA指的是现场可编程门阵列,它的基本功能模块是由N输入的查找表,存储数据的触发器和复路器等组成。在正确的设置下,这三个部分各司其职。查找表能够通过对数据的读取实现输入数据的任意布尔函数;触发器则用来存储数据,如有限状态机的状态信息;复路器可以选择不同的输入信号进行组合,将查找表和触发器用可编程的布线资源连接起来,可以实现不同的组合逻辑和时序逻辑。由于FPGA内部结构的特点,它可以很容易地实现分布式的算法结构,这一点对于实现无线通信中的高速数字信号处理十分有利。因为在无线通信系统中,许多功能模块通常都需要大量的滤波运算,而这些滤波函数往往需要大量的乘和累加操作。而通过FPGA来实现分布式的算术结构,就可以有效地实现这些乘和累加操作。
目前,无线通信一方面正向话音和数据综合的方向发展,另一方面迫切需要将移动技术综合到手持PDA产品中去。因此,随着无线移动通信系统的发展,以及对更为完善的便携式系统的期望,构架系统模块的处理器就必须更加地强有力。这一要求对无线通信的FPGA芯片市场提出了重要的挑战,其中最重要的三个方面是FPGA的功耗、性能和成本。目前已有许多研究来平衡这三方面的要求,如利用系统芯片(SOC)可以将尽可能多的功能集成在一片FPGA芯片上或FPGA芯片集上,使其性能上具有速率高、功耗低;在成本上价格低廉;而且还可以降低复杂性,便于使用。
特别是在无线通信领域里,SOC由于具有极强的实时性,使其对话音进行实时处理成为可能;由于它是通过面向芯片结构的软件编程来实现其功能的,因而仅修改软件而不需改硬件平台就可以改进系统原有设计方案或原有功能,因而具有极大的灵活性;又由于这种情况下的FPGA芯片并非专门为某种功能设计的,因而使用范围广、产量大、价格可以降到很低。所以FPGA将会越来越多地应用于无线通信系统中,它的优良性能将会促进无线通信的发展;而带来的无线通信蓬勃发展又将会进一步促进FPGA技术的不断进步。
对于现有移动通信中的许多关键技术,如:CDMA技术,软件无线电,多用户检测等技术都需要依靠高速、高性能的并行处理器来实现。随着这些应用的日益多样化,FPGA已经不再是一块独立的芯片,而演变成了构件内核。这使得设计师能选择合适的内核,与专用逻辑“胶结”在一起形成专用的FPGA方案,以满足信号处理的需要。目前还出现把DSP核和FPGA集成在一起的芯片。FPGA芯片的一些具体应用方面,如:用于实现语音合成,纠错编码,基带调制解调,以及系统控制等功能;基于DSP核矢量编码器用于将语音信号压缩到有限带宽的信道中;用来实现基带调制解调功能;另外还有定时的恢复、自动增益和频率控制、符号检测、脉冲整形、以及匹配滤波器等。
特别是对于其中的调制解调器,由于需要大量的复杂数学运算,并且对调制解调器的大小、重量、功耗特别关注,这就对FPGA的要求就更高,调制解调器的速度随FPGA的速度的提高而不断提高。FPGA在通信领域的应用,大大改善了现代通信系统的性能,也极大地推动了SOC的发展。但对于当今的移动通信设备,一片FPGA难以达到系统级处理的能力。比如现在的第三代移动通信,一片FPGA只能进行信源和信道方面的物理层处理,不能处理控制和高层信令。只有与另外的DSP或者CPU相结合才能完成整个任务。因此,基于DSP/CPU加FPGA的网络产品将成为未来的应用热点。随着移动通信的宽带GSM,CDMA标准的转移和高速数据传送网络对XDSL的要求,基于内嵌DSP/CPU的FPGA SOC将更有前途。
专家指出,今后高速DSP/CPU加FPGA技术的发展趋势,将是以系统芯片为核心,信息处理速度将达到每秒几十亿次乘加运算,因此,只有多系统芯片才能肩负此重任。嵌入式系统已经与SOC技术融合在一起,成为新一代信息技术的基础。基于DSP/CPU加FPGA的嵌入式系统不仅具有其他微处理器和单片机嵌入式系统的优点和技术特性,而且还可能利用并行算法操作,具有更高速的数字信号处理能力,为实现系统的实时性提供了更为有利的支持。DSP/CPU加FPGA系统必将成为现在以及未来无线通信技术的重要支柱。
怎么用FPGA做算法
FFT算法除了必需的数据存储器ram和旋转因子rom外,仍需较复杂的运算和控制电路单元,即使现在实现长点数的FFT仍然是很困难。本文提出的FFT实现算法是基于FPGA之上的,算法完成对一个序列的FFT计算,完全由脉冲触发,外部只输入一脉冲头和输入数据,便可以得到该脉冲头作为起始标志的N点FFT输出结果。这个算法实现的可以是基2/4混合基FFT,也可以是纯基4FFT和纯基2FFT运算。
傅立叶变换和逆变换
对于变换长度为N的序列x(n)其傅立叶变换可以表示如下:
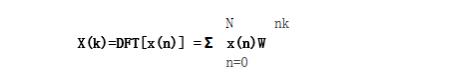
其中,W=exp(-2π/N)。当点数N较大时,必须进行分解,以短点数实现长点数的变换。而IDFT的实现在DFT的基础上就显得较为简单了:
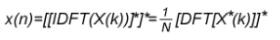
由第二个可以看出,在FFT运算模块的基础上,只需将输入序列进行取共轭后再进行FFT运算,输出结果再取一次共轭便实现了对输入序列的IDFT运算,因子1/N对于不同的数据表示格式具体实现时的处理方式是不一样的。IDFT在FFT的基础上输入和输出均有一次共轭操作,但它们共用一个内核,仍然是十分方便的。
基4和基2
基4和基2运算流图及信号之间的运算关系如图1所示:

以基4为例,令A=r0+j×i0;B=r1+j×i1;C=r2+j×i2;D=r3+j×i3;
Wk0=c0+j×s0:Wk1=c1+j×s1;Wk2=c2+j×s2;Wk3=c3+j×s3。分别代入图1中的基4运算的四个等式中有:
A‘=[r0+(r1×c1-i1×s1)+(r2×c2-i2×s2)+(r3×c3-i3×s3)]+j[i0+(i1×c1+r1×s1)+(i2×c2+r2×s2)+(i3×c3+r3×s3)] 式(3)
B’=[r0+(i1×c1+r1×s1)-(r2×c2-i2×s2)-(i3×c3+r3×s3)]+j[i0-(r1×c1-i1×s1)-(i2×c2+r2×s2)+(r3×c3-i3×s3)] 式(4)
C‘=[r0-(r1×c1-i1×s1)+(r2×c2-i2×s2)-(r3×c3-i3×s3)]+j[i0-(i1×c1+r1×s1)+(i2×c2+r2×s2)-(i3×c3+r3×s3)] 式(5)
D’=[r0-(i1×c1+r1×s1)-(r2×c2-i2×s2)+(i3×c3+r3×s3)]+j[i0+(r1×c1-i1×s1)-(i2×c2+r2×s2)-(r3×c3-i3×s3)] 式(6)
可以看出有多个公共项和类似项,这一点得到充分利用之后可以大大缩减基4和基2运算模块中的乘法器的个数,如上面A‘至D’的四个等式中的这三对类似项:(r1×c1-i1×s1)与(i1×c1+r1×s1)、(r2×c2-i2×s2)与(i2×c2+r2×s2)、(r3×c3-i3×s3)与(i3×c3+r3×s3)以高于输入数据率的时钟进行时分复用,最终可以做到只需要3个甚至1个复数乘法器便可以实现。
基2运算之所以采用图1-(b)中的形式进行基2运算,是为了将基本模块做成基4/2复用模块,它对于N有着更大的适用性和可借鉴性。在基4、基2和基4/2模块的基础上,构建基16、基8和基16/8模块有着非常大的意义。
算法实现
傅立叶变换实现时首先进行基2、基4分解,一般来说,如果算法使用基4实现,虽然使用的资源多了一些,但速度上的好处足以弥补。如果资源充足,使用基16、基8或基16/8复用模块,速度可以大大提高。一般FFT实现简单框图如图2所示。
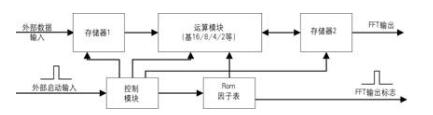
在图2中,运算模块即为基2/4/8/16模块或它们的复用模块,Rom表中存储的是N点旋转因子表。控制模块产生所有的控制信号,存储器1和2的读写地址、写使能、运算模块的启动信号及因子表的读地址等信号。当然对于运算模块为基16/8复用模块时,控制模块就需要产生模式选择信号,如对于运算模块是基4/2模块时,该信号就决定了内部运算模块是进行基4运算还是基2运算。
存储器1作为当前输入标志对应输入N点数据的缓冲器,存储器2作为中间结果存储器,用于存储运算模块计算出的各Pass的结果。在图中的各种地址、使能和数据的紧密配合下,经过一定延时后输出计算结果及其对应指示标志。
图2只是一定点或浮点的FFT实现模块,如果是块浮点运算,则必须加入一个数据因子控制器,控制每遍运算过程中的数据大小,并根据各个Pass的乘性因子之和的大小,对最终输出进行大小控制,以保证每段FFT运算输出增益一致。
-
FPGA做深度学习能走多远?2024-09-27 1457
-
FPGA在视频编码方面的应用有大佬做过吗?2024-07-29 8053
-
fpga在通信方面的应用2024-03-27 2330
-
FPGA图像处理之CLAHE算法2024-01-04 3916
-
hash算法在FPGA中的实现(1)2023-09-07 1968
-
使用FPGA做的开源示波器2023-08-29 2312
-
怎么用FPGA做算法 如何在FPGA上实现最大公约数算法2023-08-16 3849
-
在FPGA上实现CRC算法的程序2016-06-07 1055
-
用FPGA做毕业设计哪方面比较好做?2016-02-29 12632
-
关于基于FPGA的视频无线传输及通信协议方面的问题,谢谢2015-01-27 6155
-
求助:小波算法的FPGA硬件如何实现2012-11-20 2885
-
实时图像处理FPGA芯片怎么选择2012-08-06 9147
-
用FPGA实现FFT算法2008-10-30 1842
-
Altera公司用FPGA做DSP算法的工具2006-03-25 1047
全部0条评论

快来发表一下你的评论吧 !

