

基于StratixⅡEP2S30484C5芯片的乘除法和开方运算算法的实现
可编程逻辑
描述
1、引言
在FPGA的开发应用中,大多数EDA软件(后面以altera QuartursII为例)都提供乘除法、开方运算的设计向导,或提供LPM宏函数,但普遍占用资源量大。而在许多信号处理应用中,要求计算精度高、资源敏感而计算时延要求并不高,这时我们需要一种保证计算正确且资源开销最低的FPGA实现方法,本文给出了实现乘除法、开方运算的FPGA串行实现算法,并与LPM宏函数进行了性价比比较。结果表明,本文给出的各算法计算准确,资源量远小于调用LPM宏函数。
2、算法描述
2.1、乘法

向左移位操作,那么乘积右移一位,相对而言可以认为乘数被放大两倍。可见Booth算法只采用加法、减法和右移操作便可计算补码数据的乘积。对乘数从低位开始判断,根据两个数据位的情况决定进行加法或减法运算,每次将乘积项向右移一位。

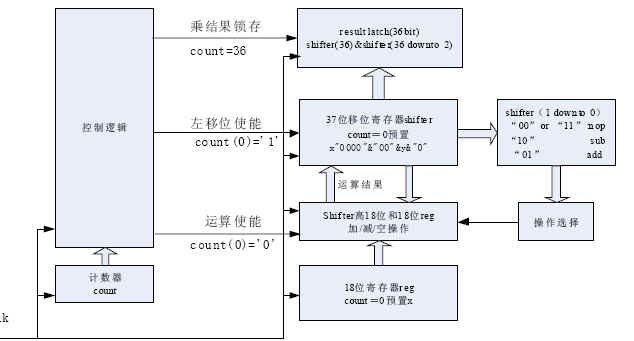
图1
实现结构如图1。可见,本算法将乘法转化为串行的加减和移位运算,从而节省了大量逻辑资源。
2.2、除法
除法计算我们采用经典的计算的方式,这种算法的实现思路清晰,实现的结构也很简单。我们首先介绍原码除法的实现。
设:A、B均为无符号数,A=1011,B=0011,求A/B。其计算如下图:

图2
其特点可归纳如下:
(1)、 每次比较余数(被除数)和除数的大小,确定商为1还是0;
(2)、 每做一次减法,保持余数不动,低位由被除数低位补进,再减去右移后的除数。
对于补码除法运算,为了简化中间判断过程,我们可以先将除数和被除数取模,然后按照原码的计算方法求出商和余数,再根据除数和被除数的符号对计算结果进行修正即可。由此可见,有符号除法包含了无符号除法的运算过程,所以我们这里也着重介绍有符号除法的计算过程。设:被除数(x)为56位,除数(y)为28位,考虑所有可能性,则商(q)取56位,余数(r)取28位。具体实现步骤如下:
(1)、56位余数移位寄存器shx=mod(x),28位余数寄存器reg=mod(y),被除数符号flagx=sign(x),除数符号flagy=sign(y), 29位余数移位寄存器shr=0,56位余数移位寄存器shq=0,k=112;
(2)、 若k为奇数, shr左移一位低位补shx最高位, shx左移一位低位补0;
若k为偶数,则 if shrelse shq左移一位低位补1,shr=shr-reg;
(3)、 重复步骤2,直到 ;
(4)、 结果修正(如表2)。
说明:最后需要根据A、D的符号和shQ、shR、regD的值对计算结果进行修正。修正方法如下表。
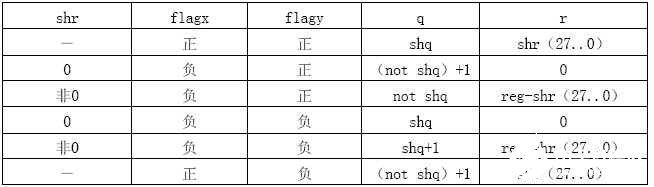
表2
本算法由于基于经典方式实现,思路清晰,同时全串行操作也很大程度上降低了资源量。
2.3、开方
非冗余算法是经典的开方算法,其基于如下计算:



图3
3、FPGA实现
我们在Altera公司的QuartusⅡ5.1软件环境下使用VHDL语言完成了上述各算法,并在StratixⅡEP2S30484C5芯片中实现。下面给出了各算法的资源消耗情况,并与IP_core作了比较(如表3)。
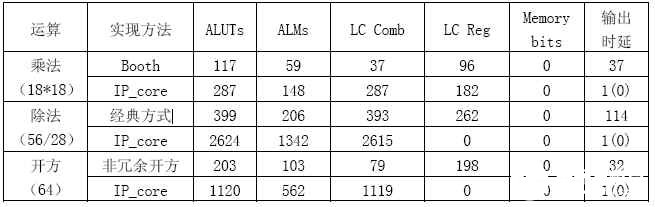
表3
可以看出本文中提出的算法对二进制数的乘除法以及开方占用资源很少,而且保证了计算精度;IP_core所用时间最短(输出时延可调),但占用逻辑单元随着位宽的增加急剧上升。由
此可见,当实际设计对逻辑单元使用要求不苛刻时,便可以使用IP_core,其设计简单且计算时
延小。若对逻辑单元使用有要求且对计算时延不敏感时,使用串行乘除法和开方是很好的选择。
4、结束语
本文给出了乘除法、开方运算的FPGA串行实现算法,与IP_core方法相比,本文中的算法占用逻辑单元少,但计算周期较长,实际应用中可以考虑采用流水线等改进办法,以进一步缩短计算周期。
责任编辑:gt
-
如何对蜂鸟e203内核乘除法器进行优化2025-10-24 171
-
乘除法运算2009-09-21 4192
-
雾盈FPGA笔记之(三十二)六位四则运算计算器(8)算法实现加减乘除2016-09-01 6374
-
灵动微电子 | MM32SPIN2x 电机专用MCU功能特色——硬件除法器与硬件开方2018-11-30 3167
-
基于CORDIC技术的无开方无除法的MQR阵分解方法2020-11-23 1696
-
基于Stratix II EP2S60改进中值滤波器的设计及实现,不看肯定后悔2021-04-23 1467
-
整数乘除法与位运算的效率对比分析哪个好2021-12-24 1327
-
Stratix II EP2S60 DSP Developm2010-04-07 744
-
乘除法和开方运算的FPGA串行实现2010-07-28 923
-
乘除法电路2010-04-26 17162
-
高效的C编程之除法运算2017-10-17 2214
-
FPGA芯片EP2S90F1508C3实现SM3算法的硬件实现策略2017-11-24 3103
-
基于delta码的乘除法运算错误检测改进算法2017-12-04 929
-
如何使用FPGA实现开方运算2020-08-06 2144
-
C语言如何用移位来解决乘除法问题2023-11-21 1778
全部0条评论

快来发表一下你的评论吧 !

