

测试脉冲响应对滤波器阶跃响应的影响
模拟技术
描述
在高性能电机和伺服驱动器中,基于隔离式sigma-delta(Σ-Δ)的模数转换器(ADC)已成为首选的相电流测量方法。这些转换器以其强大的电流隔离和卓越的测量性能而闻名。随着新一代ADC的推出,其性能也在不断提高,但是,要充分利用最新的ADC的功能,就需要对其他的电机驱动器进行相应的设计。
简介
电机驱动器制造商不断提高其产品的性能和鲁棒性。一些改进是通过采用更先进的控制算法和更高的计算能力实现的。其他改进则通过最小化反馈电路中的非理想效应来实现,比如延迟、倾斜和温度漂移。
就电机控制算法的反馈而言,最关键的部分是相电流的测量。随着控制性能提高,系统对时序精度、偏移/增益误差、多反馈通道的同步等非理想效应越来越敏感。多年来,半导体公司一直致力于减少反馈信号链中的这些非理想效应,而且这种趋势很可能会持续下去。ADuM7701就是为测量相电流而优化的最新一代隔离式Σ-ΔADC示例。虽然ADC的性能很重要,但也很可能在反馈路径的其余部分造成非理想效应。本文不考虑ADC,主要讨论反馈路径的其余部分。虽然本文着重介绍电机控制应用,但它也适用于任何需要Σ-ΔADC紧密同步的其他系统。
使用Σ-ΔADC时的典型信号链如图1所示。模拟输入电压通过让相电流通过一个电阻分流器来产生。Σ-ΔADC将模拟信号转换成1位数据流,并提供电气隔离,因此ADC之后的一切都与电机相电位隔离。转换器之后是通过滤波方式执行的解调。该滤波器将1位信号转换为多位(M位)信号,并通过抽取过程降低数据更新速率。虽然滤波器抽取降低了数据速率,但速率通常仍然过高,无法匹配控制算法的更新速率。为了解决这个问题,我们增加了最后的降采样阶段。
本文假设滤波器和抽取级在FPGA中实现,并且滤波器是一个三阶sinc滤波器(sinc3)。
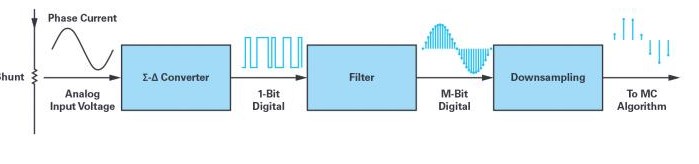
图1.一种用于测量相电流的∑-∆信号链。
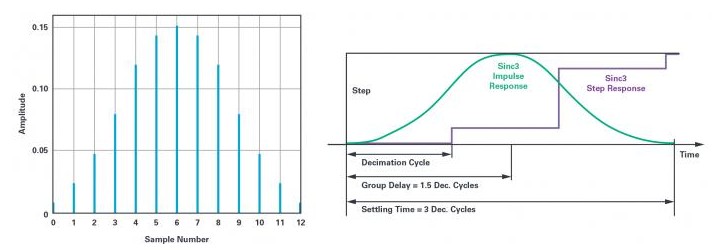
图2.(a)滤波器抽取率为5的sinc滤波器脉冲响应。(b)Sinc滤波器的阶跃响应以及与脉冲响应的关系。
Sinc滤波器同步
Σ-ΔADC和sinc滤波器的缺陷在于很难在同一个时域中进行控制,并且缺少指定的采样时刻。2与具备专用的采样保持电路的传统ADC相比,这两种滤波器都有一些令人担忧的地方。不过也有办法解决这个问题。如本节所示,将sinc滤波器与系统的其余部分同步,并在适当的时刻采样相电流至关重要。如果未能正确做到这一点,测量结果将会大幅失真。
sinc滤波器的输出并不代表该时刻Σ-ΔADC的输入。相反,输出是过去窗口期间输入的加权平均值。这是由滤波器的脉冲响应造成的。图2a显示了抽取率为5时sinc3的脉冲响应。从图中可以看出,滤波器输出如何成为输入序列的加权和,中间的采样获得较大权重,而序列开始/结束时的采样权重较低。
在继续讨论之前,需要给出几个基本定义。Σ-ΔADC时钟,又称为调制器时钟,表示为fmod。抽取率(DR)决定抽取频率(fdec),并与fmod关联:
图2右侧显示了脉冲响应对滤波器阶跃响应的影响。应用该步骤时,滤波器输出不受影响,滤波器在3个完整的抽取周期之后达到稳定状态。因此,sinc3滤波器的一些重要特性可以表述为:
►群延迟为1.5个抽取周期
►建立时间为3个抽取周期
在将滤波器与控制系统同步时,这些属性非常重要,本文将始终会用到。
在讨论sinc滤波器同步之前,必须先定义输入信号的特性。这反过来又会定义滤波器的同步特性。
图3显示了由电压源逆变器驱动的3相永磁电机的模拟相电流。调制方式为空间矢量PWM3,开关频率为10kHz。将电机加载到5A峰值相电流和3000rpm转速。这种设置加上3个极对数,可以得到6.67ms电气基本周期。
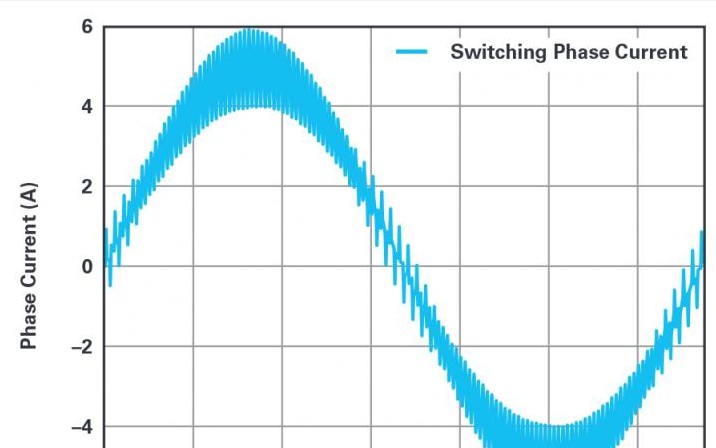
图3.采用空间矢量脉宽调制时的电机相电流。
相电流可以看作由两个分量组成:平均分量和开关分量。出于控制目的,仅关注电流的平均分量,因此必须完全去除开关分量。要提取平均分量,最常见的方法是对与PWM同步的信号(用于电机终端)进行采样。如图4所示。最上面的信号显示相电流的开关波形,中间的信号显示对应的逆变器相位臂的高端PWM,最下面的信号显示来自PWM定时器的同步信号。PWM同步信号在PWM周期的开始和中间进行置位。为简明起见,假设所有三相的占空比都是50%,意味着电流只有一个上升斜坡和一个下降斜坡。在PWM同步信号的上升沿,电流取其平均值,因此如果恰好在那一刻采样电流,开关分量将被完全抑制。实际上,采样保持电路相当于一个在开关频率上具有无限衰减的滤波器。
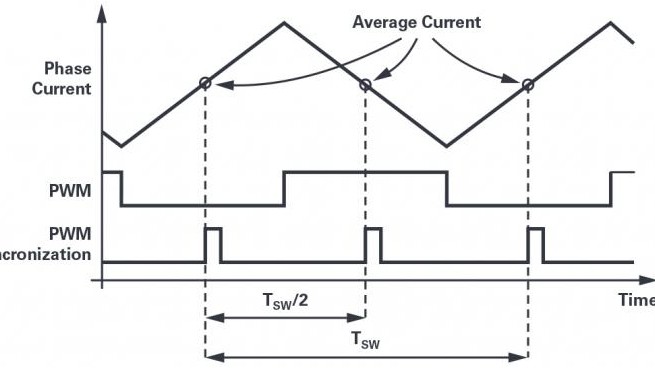
图4.在PWM周期的起始点和中心点处测量相电流会减弱电流纹波。
图5显示了将这种采样应用于图3中所示波形时的结果。右侧所示是实际相电流和采样电流的波形放大图。注意采样保持过程如何完全消除纹波。
采样电流以每单位表示,其中0A映射到0.5,全比例值为8A。选择这个比例是为了更容易与后面的∑-∆测量值进行比较。图5所示的结果为理想场景,采样后只剩下基波分量。因此,可以将这些数据当做比较∑-∆测量值的基准值。
∑-∆测量和混叠
在理想的采样保持ADC中,由于严格控制采样时刻,所以能够提取基波分量。然而,Σ-∆转换是一个连续的采样过程,纹波分量将不可避免地成为测量的一部分。
在Σ-∆转换中,抽取率与信噪比(SNR)之间存在密切联系。抽取率越高,输出的有效位数(ENOB)越多。缺点是,随着抽取率增加,群延迟也会增加,因此设计者必须在信号分辨率和反馈链的延迟之间折中考量。一般来说,与控制周期相比,应将延迟保持在较小范围。对于电机控制,典型的抽取率在128到256之间,这可以很好地平衡信噪比和群延迟。
在数据手册规范中,通常使用256作为抽取率。例如,ADuM7701的ENOB为14位,抽取率为256。ENOB值如此高时,预计可以得到非常准确的测量结果。为了验证这一点,假设图3所示的相电流是采用Σ-ΔADC在20MHz时测量所得,数据流则由使用256抽取率的sinc3进行解调。结果如图6a所示。
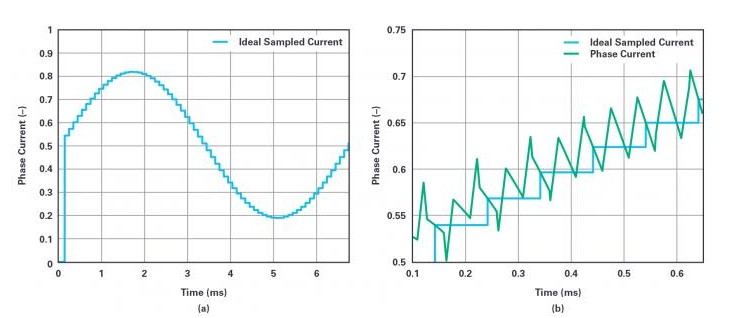
图5.理想的相电流采样:(a)理想的采样相电流的基波周期,(b)相电流和采样相电流的波形放大图。
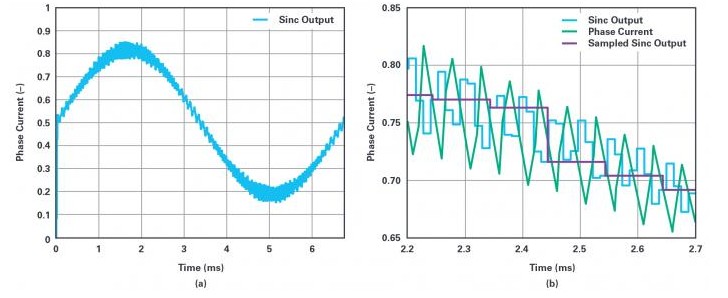
图6.(a)sinc滤波器的输出。(B)实际的相电流和sinc滤波器抽取输出的波形放大图。
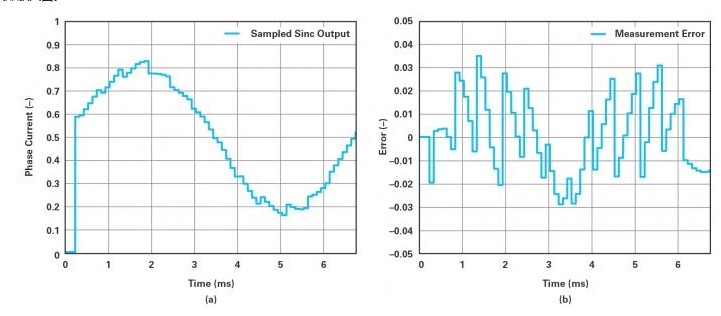
图7.(a)sinc滤波器的采样输出。(b)测量误差。
相电流的基波分量非常明显,但与图5a所示的理想采样相比,测量信号存在很大的噪声。因此,虽然ADC和sinc滤波器本身提供了不错的ENOB数量,但反馈信号的质量却很差。从图6b可以看出其原因,该图是sinc滤波器输出和实际的相电流的波形放大图。注意相电流的10kHz开关分量是如何发生相移,以及几乎未被sinc滤波器衰减。现在,假设在每个PWM周期执行一次电机控制算法,并在周期开始时读取最新的sinc滤波器输出。实际上,sinc滤波器的输出会向下采样,以匹配控制算法的更新速率。向下采样和得到的信号在图6b中显示为采样sinc输出。图7a显示了按照PWM速率滤波和采样的整个基波周期的结果。
很明显,相电流测量失真严重,因此控制性能会非常差。如此,应该增加扭矩波纹,并且需要降低电流控制环路的带宽。从理想测量值(图5a)中减去图7a中的测量值,就可以得到误差(图7b)。误差约为原比例信号的7%,与预期的14ENOB相差甚远。
这个Σ-Δ测量和混叠场景演示了基于Σ-Δ的非常常见的电流测量模式,以及它是如何引导设计人员得出“Σ-ΔADC不适合电机驱动器”这个结论的。但是,这个示例并没有显示出ADC本身的糟糕性能。相反,因为未能正确设置相电流测量值,所以余下信号链的性能欠佳。
ADC在几兆赫(一般为10MHz至20MHz)下对输入信号采样,在抽取率为256时,sinc滤波器有效去除调制噪声。在如此高的采样率下,滤波器输出中存在相电流纹波分量,在信号链的向下采样级,这可能成为一个问题(见图1)。如果纹波分量没有充分衰减,且电机控制算法以PWM速度消耗电流反馈,则结果会因为降采样而产生混叠。
根据标准采样理论,为了避免混叠,信号在一半采样频率以上时必须无能量。如果对Σ-ΔADC输出向下采样至10kHz,那么5kHz或更高频率下的噪声将会混叠到测量值中。如图所示,在sinc滤波器之后,信号中还存在大量10kHz开关噪声。降低10kHz噪声的一种方法是增加抽取率,但是这样做会导致不可接受的长时间群延迟。我们需要采用一种不同的方法。
通过同步改善测量
上一节讨论的抗混叠方法的主要问题如图8所示。sinc滤波器的输出在与相电流开关分量无关的某个时刻被读取。输出信号被读取时,滤波器根据脉冲响应对输入信号进行加权平均。这个加权平均值有时跨越开关波形的低点,有时跨越高点。因此,用作反馈的信号含有明显噪声,频率从0Hz到PWM频率的一半。
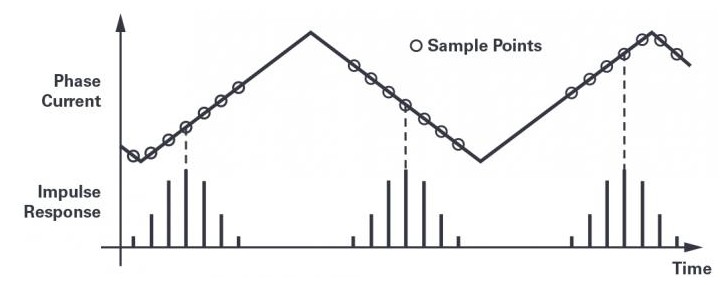
图8.脉冲响应与开关波形无关。
Σ-ΔADC连续采样,sinc滤波器输出乘以每个PWM周期的测量值(通常10到20)。由于每次测量跨越3个抽取周期,所以脉冲响应会重叠。为了简化起见,图8中仅显示三个测量/脉冲响应。
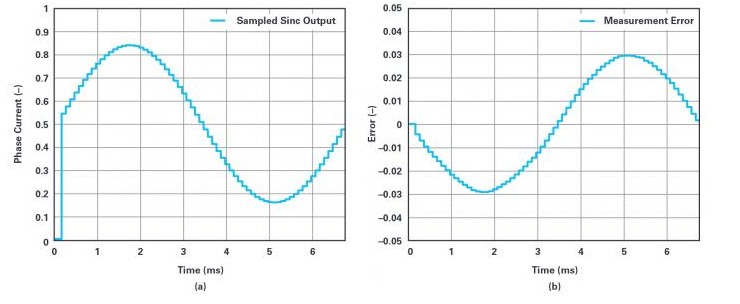
图9.(a)脉冲响应锁定采用PWM时,sinc滤波器的采样输出。(b)测量误差。
问题的根源在于:脉冲响应没有锁定为电流的开关分量,而开关分量又被锁定为PWM。解决方案是选择抽取率,使每个PWM周期都有固定的整数抽取周期。例如,如果PWM频率为10kHz,调制器时钟为20MHz,抽取率为200,那么每个PWM周期正好有10个抽取周期。每个PWM周期有固定的采样周期,脉冲响应始终锁定为PWM,用于反馈的测量值在PWM周期内的同一点被捕获。采用这种同步方案的相电流测量如图9a所示。
显然,将响应同步与PWM同步会产生积极的影响。噪声会被消除,且乍一看,测量结果似乎与图5a中的理想测量值相似。但是,用理想测量值减去∑-∆测量值时,就会得出图9b所示的误差信号。误差大小与图7b中所示的值相似,但频谱发生了变化。现在,误差是一阶谐波,相当于增益误差。导致这种错误模式的原因如图10所示。
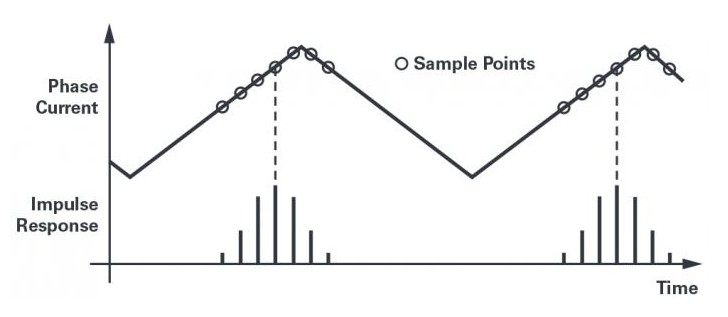
图10.脉冲响应被锁定为开关周期内的某个固定点。
虽然消除了白噪声误差分量,但由于测量值受到开关分量的影响,信号仍然是失真的。在图10中,注意sinc滤波器的脉冲响应如何围绕开关波形的峰值给出加权平均值。根据脉冲响应相对于PWM的相位,偏差的大小仅受纹波电流的大小限制。如图3所示,纹波分量的幅值在基波周期内发生变化,基波电流峰值时纹波最高,过零点时纹波最低。因此,测量误差为一阶谐波分量。
为了消除一阶谐波测量误差,脉冲响应必须始终以PWM周期的起始点或中心为中心,此时相电流正好等于其平均值。图11显示了以开关周期的起始点为中心的脉冲响应。在这一点周围,开关波形是对称的,因此,通过在每一边都有相同数量的测量点,纹波分量在这一点周围均为零。
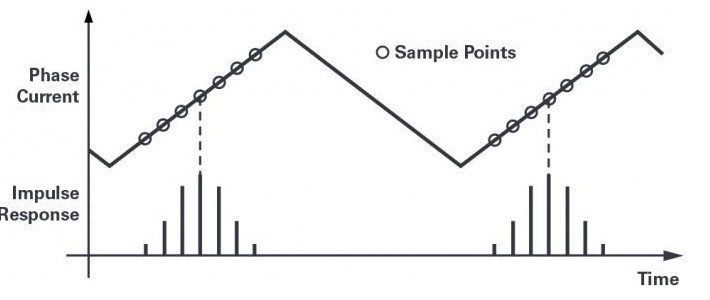
图11.脉冲响应锁定为开关周期,并对准理想的测量点。
脉冲响应锁定,以平均电流的时刻为中心时,测量结果如图12a所示,测量误差如图12b所示。作为理想的采样测量,该信号不存在白噪声和增益误差。
结果表明,∑-∆测量值的质量不仅仅取决于抽取率。只有在无混叠时,普遍认为“增加抽取率会提高ENOB”的这种观点才是正确的。控制滤波器相对于输入信号的更新率和相位比抽取率更重要。例如,比较图7(基于256的抽取率)和图12(基于200的抽取率)。降低抽取率可显著改善测量结果。
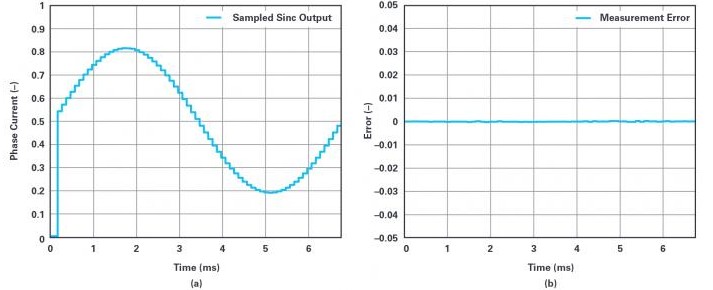
图12.(a)脉冲响应锁定采用PWM,且以平均电流时刻为中心时,sinc滤波器的采样输出。(b)测量误差。
结论
综上所述,实现基于∑-∆的优化相电流测量值的条件如下:
►三阶sinc滤波器的脉冲响应时间为3个抽取周期,这意味着数据需要3个抽取周期才能通过滤波器。
►滤波器的脉冲响应必须以平均电流时刻为中心。
►脉冲响应的1.5个采样周期必须在平均电流时刻之前,另外1.5个采样周期必须在平均电流时刻之后。
►sinc滤波器在PWM周期内产生多个输出,但只使用其中一个输出。其余的输出都被忽略。
责任编辑:pj
-
关于高斯滤波器的响应和逼近2023-04-28 5518
-
无限脉冲滤波器的设计2014-07-10 3943
-
FTR滤波器_滤波器原理_有限脉冲响应滤波器_明德扬fpga2017-08-02 4169
-
有源滤波器相位响应2019-10-14 1833
-
请问怎么用滤波器实现滤除单位脉冲响应的某些频率部分2019-11-09 3338
-
模拟低通滤波器和数字有限脉冲响应滤波器有何不同2021-07-29 2404
-
ADA4961脉冲响应异常怎么解决?2023-11-14 790
-
数字信号处理实验指导 -无限长单位脉冲响应(IIR)滤波器的2009-05-10 985
-
基于无限脉冲响应数字滤波器的优化迭代学习控制器设计方法2017-12-07 962
-
TL431脉冲响应时间测试2017-12-12 7825
-
数字信号处理教程之有限脉冲响应滤波的详细课件免费下载2019-11-13 1230
-
有源滤波器中的相位响应2023-01-06 3649
-
远红外滤波器的工作原理/优点/应用2023-03-08 2449
-
滤波器介绍及系数设计2023-06-02 11252
-
如何使用Python中的SciPy库计算系统的脉冲响应?2023-06-20 4301
全部0条评论

快来发表一下你的评论吧 !

