

浅谈电路布线电路设计
电子说
描述
《算法设计与分析》 --王晓东
题目描述:
在一块电路板的上、下2端分别有n个接线柱。根据电路设计,要求用导线(i,a(i))将上端接线柱与下端接线柱相连,其中a(i)表示上端点i对应的向端点的值。如图所示:
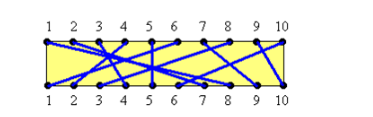
题目要求是在给定的连线中,选取不相交连线的最大子集,即不相交连线的最大数目。并把最大不相交子集的情况给列举处理啊。
解题思路:
首先用a[i]数组表示与上面对应点相连线的下面的点,再用set[i][j]表示上面节点i与下面节点j连线的左边(包括i j连线)的最大不相交连线的个数。
于是就有公式:
max(set[i-1][j], set[i][j-1]); j != a[i]
set(i,j) =
set[i-1][j-1] + 1; j == a[i]
然后就可以对每一个i,都对所以的j求一遍。这样就可以得出结果吗,set[n][n]即我们想要的结果。
最后通过回溯把结果输出出来。
代码实现:
#include 《stdio.h》
#define MAX(a,b) ((a) 》 (b) ? (a) : (b))
void circut(int a[],int set[][11],int n);
void back_track(int i,int j,int set[][11]);
int main()
{
int a[] = {0,8,7,4,2,5,1,9,3,10,6};
int set[11][11];
circut(a,set,10);
printf(“max set: %d \n”,set[10][10]);
back_track(10,10,set);
printf(“\n”);
return 0;
}
void circut(int a[],int set[][11],int n)
{
int i,j;
for (i = 0; i 《 n; i++)
{
set[i][0] = 0;
set[0][i] = 0;
}
for (i = 1; i 《= n; i++)
{
for (j = 1; j 《= n; j++)
{
if (a[i] != j)
set[i][j] = MAX(set[i-1][j],set[i][j-1]);
else
set[i][j] = set[i-1][j-1] + 1;
}
}
}
void back_track(int i,int j,int set[][11])
{
if (i == 0)
return;
if (set[i][j] == set[i-1][j])
back_track(i-1,j,set);
else if (set[i][j] == set[i][j-1])
back_track(i,j-1,set);
else
{
back_track(i-1,j-1,set);
printf(“(%d,%d) ”,i,j);
}
}
-
FPGA布线开关的电路设计2011-03-02 3375
-
承接电路设计,pcb布线。价格实惠质量可靠2014-03-03 4726
-
高频电路设计布线技巧2017-11-15 2696
-
高频电路设计布线技巧概述!2019-09-05 1594
-
高频电路设计的布线技巧2019-10-12 1640
-
开关电源 PCB电路设计中的接地与布线.pdf2020-07-31 5871
-
经典资料分享之PCB电路设计中的接地与布线2020-08-20 5449
-
高频电路布线技巧2009-03-25 1346
-
PCB电路设计中布线的EMC分析2016-07-29 1285
-
浅谈RF电路设计2018-03-12 8471
-
电路板厂布线设计的顺序2020-06-04 3370
-
讲解高速PCB的布线、布局和电路设计2020-07-10 1214
-
如何解决高频电路的布线2020-11-02 806
-
电源电路布局布线如何进行2023-11-06 1188
-
高频电路设计布线技巧十项规则【转】2023-12-11 1250
全部0条评论

快来发表一下你的评论吧 !

