

利用低功耗微控制器开发FFT应用
应用电子电路
956人已加入
描述
摘要:今天的低功耗微控制器(μC)也开始集成原先只存在于大型微处理器、ASIC和DSP中的外设功能,使我们有可能以很低的功耗实现复杂的算术运算。本文讨论一种快速傅立叶变换(FFT)应用,并在一个含有单周期硬件乘法器的低功耗μC上实现该应用。
这个FFT应用实时计算一路输入电压(图1中的VIN)的频谱。为完成该任务,用一片模数转换器(ADC)对VIN进行采样,获得的采样传送给µC。然后,µC对这些采样执行256点FFT运算,获得输入电压的频谱。为便于检测,µC将计算出的频谱数据传送给PC,由PC实时显示出来。
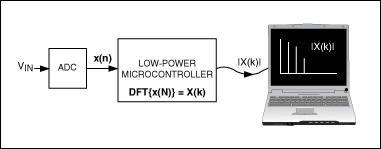
图1. 利用FFT应用计算输入电压的频谱。
该FFT应用的固件针对MAXQ2000系列中的一款16位、低功耗µC用C语言编写。有兴趣的读者可以下载(ZIP,2.4kb)该项目的固件和电路原理图。

其中N是采样的数量,X(k)是频谱,x(n)是一组输入采样。利用欧拉等式展开求和符,并分离输入采样和频谱的实部和虚部,得到以下等式:


式2和3中,求和符中第二项的消失是由于输入采样全部为实数。假定我们有N个采样,直接计算式2和3需要2N²次乘法和2N(N - 1)次加法。这样,我们的256点输入采样DFT将需要进行131,072次乘法和130,560次加法运算。我们还是将注意力转向FFT吧!
有多种FFT算法可供使用。本应用采用普通的radix-2算法,继续将DFT分解为两个更小的DFT。为此,N必须是2的指数。这种radix-2 FFT算法的步骤可归纳如图2所示的蝶型运算。观察这些蝶型运算我们可以发现,radix-2算法仅需(N / 2)log2(N)次乘法和Nlog2(N)次加法。图2中用到的参数WN就是通常所谓的“旋转因子”,可以在执行算法前预先计算出来。
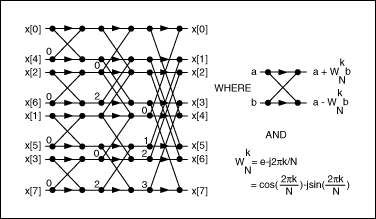
图2. 利用蝶型运算实现N = 8的FFT。
在图2中,FFT的输入显示为一种特殊的排列顺序,这种序列是对原始序列索引号的二进制位反转后得到的。因此,当我们对N = 8个采样执行radix-2 FFT算法时,需要将输入数据的原始序列:
0 (000b), 1 (001b), 2 (010b), 3 (011b), 4 (100b), 5(101b), 6(110b), 7(111b)
重新排列为:
0 (000b), 4, (100b), 2 (010b), 6 (110b), 1 (001b), 5 (101), 3 (011), 7 (111)
FFT输出则以正确的顺序排列。图2还说明,每个单独的蝶型运算所得的结果,是下一级FFT运算所需的唯一数据。由于运算过程可“即位”进行,新值可替代旧值,这样,计算N个采样的FFT只需要2N个变量(因为每个数据都包括实部和虚部两部分)。
FFT完成后,结果为复数形式。式4和5将结果转换为极坐标方式后表示为:


有关DSP的文献中可以找到很多优化方法,可使上述DFT/FFT算法更小或更快。其中最重要的一种优化方法(可能也是最容易实现的)源于这样一个事实,那就是作为一个实数信号,其DFT幅度是相关于X(N / 2)对称的,因此:

编写FFT代码绝非易事。低功耗µC的一些局限又进一步使该任务复杂化。
存储器:我们所选的µC有2kB的RAM。已经知道该算法需要用到2N个16位变量来存储FFT数据,这样,我们的µC可以执行N最高为512的FFT。然而,固件的其他部分也要用到一些RAM。因此,在此项目中,我们限制N于256。若采用16位变量来表示每个值的实部和虚部,FFT数据总共需要1024字节的RAM。
速度:低功耗µC尽管具有高MIPS/mA性能,仍然需要一些优化手段来使运行FFT的指令数尽可能少。好在本应用所用的C编译器(IAR的Embedded Workbench for MAXQ,见www.iar.com)可提供多种级别的优化和设置。高效地使用硬件乘法器可使代码优化到可以接受的水平。
无浮点能力:所选的µC不具备浮点能力(低功耗产品一般都不具备浮点能力)。因此,所有运算都必须采用定点算法。为了表示小数,固件采用带符号的Q8.7表示法。这样,在固件中假定:

所选的数据表示法还要适应FFT算法可能遇到的最大数值,同时又要提供足够的精度。例如,我们的ADC可提供带符号的8位采样,以二的补码表示。如果输入为最大幅度(对于带符号8位采样为127)的直流电压,则其能谱全部包含于X(0)中,用Q8.7表示为32512。这个数值能够由单个带符号的16位数据表示。
ADC采样循环中的判决语句会造成采样间隔的抖动。例如,我们的系统从ADC读取带符号的8位采样,并将其存储在一组16位变量中。在下面的程序清单1中给出了两种伪码算法,执行这种ADC读取-存储功能。算法1给出的方法会造成采样间隔的抖动,因为负采样比正采样需要更多的时间来读取并存储。
清单1. 两种ADC采样伪码算法。第二种算法避免了第一种的问题――采样间隔抖动。
清单2. 正弦和余弦函数LUT。
清单3. 用于实现N = 256的位反转的展开循环。
FFT算法的核心部分是执行蝶型运算的一小块代码。程序清单4给出了这一块代码,遗憾的是,它是本应用中唯一“不可移植”的固件。宏MUL_1和MUL_2利用µC的硬件乘法器执行单指令周期乘法运算。这些宏的内容专用于MAXQ2000,可在实际固件中全部看到。
清单4. 用C编写的蝶型运算。
清单5. FFT结果从复数形式转换为极坐标形式。
从式6我们已经知道,频谱的幅度是关于X(N / 2)对称的,因此我们只需将前(N / 2) + 1个频谱数据转换为极坐标形式。还有,我们可以看到,对于实数输入采样,X(0)和X(N / 2)的虚部总为零。因此这两条谱线的幅度被单独计算。本项目实际固件的注释中包含了用于自动生成该LUT的源代码,可由程序调用来计算X(k)的幅度。


程序清单6给出了实现这些函数的代码。同样,本项目实际固件的注释中包含了用于自动生成这些LUT的源代码,可由程序调用来实现这些窗函数。
清单6. 用来实现Hamming和Hann窗函数的LUT。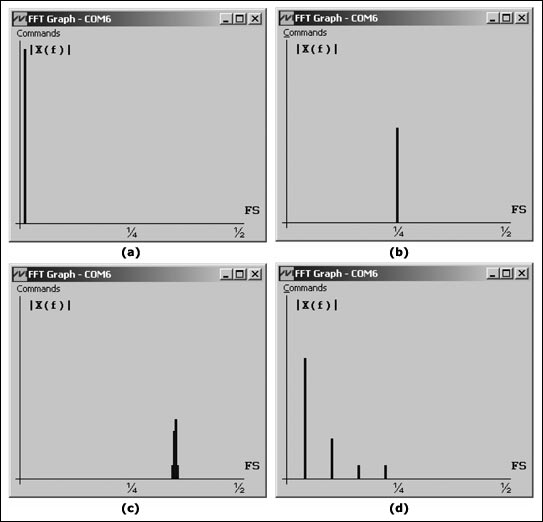
图3. FFT Graph软件显示的由低功耗µC计算出的频谱。
总之,本文所讨论的算法对于低功耗µC上的FFT应用而言,提供了一个很好的出发点。如果想了解更多信息和具体实现的细节,请查阅我们为本应用所提供的、带有详细注释的固件信息。
Lemieux, Joe, Fixed-point math in C, Embedded Systems Programming, 2003年10月。
Proakis, John G.和Dimitris G. Manolakism, Digital Signal Processing Principles, Algorithms, and Applications, 第3版, Prentice Hall, 1996。
Smith, Steven W., The Scientist and Engineer's Guide to Digital Signal Processing, 第2版, California Technical Publishing, 1999。
打开APP阅读更多精彩内容
这个FFT应用实时计算一路输入电压(图1中的VIN)的频谱。为完成该任务,用一片模数转换器(ADC)对VIN进行采样,获得的采样传送给µC。然后,µC对这些采样执行256点FFT运算,获得输入电压的频谱。为便于检测,µC将计算出的频谱数据传送给PC,由PC实时显示出来。

图1. 利用FFT应用计算输入电压的频谱。
该FFT应用的固件针对MAXQ2000系列中的一款16位、低功耗µC用C语言编写。有兴趣的读者可以下载(ZIP,2.4kb)该项目的固件和电路原理图。
背景知识
为确定输入信号采样的频谱,我们需要对这些输入采样进行离散傅立叶变换(DFT)。DFT的定义如下:
其中N是采样的数量,X(k)是频谱,x(n)是一组输入采样。利用欧拉等式展开求和符,并分离输入采样和频谱的实部和虚部,得到以下等式:


式2和3中,求和符中第二项的消失是由于输入采样全部为实数。假定我们有N个采样,直接计算式2和3需要2N²次乘法和2N(N - 1)次加法。这样,我们的256点输入采样DFT将需要进行131,072次乘法和130,560次加法运算。我们还是将注意力转向FFT吧!
有多种FFT算法可供使用。本应用采用普通的radix-2算法,继续将DFT分解为两个更小的DFT。为此,N必须是2的指数。这种radix-2 FFT算法的步骤可归纳如图2所示的蝶型运算。观察这些蝶型运算我们可以发现,radix-2算法仅需(N / 2)log2(N)次乘法和Nlog2(N)次加法。图2中用到的参数WN就是通常所谓的“旋转因子”,可以在执行算法前预先计算出来。

图2. 利用蝶型运算实现N = 8的FFT。
在图2中,FFT的输入显示为一种特殊的排列顺序,这种序列是对原始序列索引号的二进制位反转后得到的。因此,当我们对N = 8个采样执行radix-2 FFT算法时,需要将输入数据的原始序列:
0 (000b), 1 (001b), 2 (010b), 3 (011b), 4 (100b), 5(101b), 6(110b), 7(111b)
重新排列为:
0 (000b), 4, (100b), 2 (010b), 6 (110b), 1 (001b), 5 (101), 3 (011), 7 (111)
FFT输出则以正确的顺序排列。图2还说明,每个单独的蝶型运算所得的结果,是下一级FFT运算所需的唯一数据。由于运算过程可“即位”进行,新值可替代旧值,这样,计算N个采样的FFT只需要2N个变量(因为每个数据都包括实部和虚部两部分)。
FFT完成后,结果为复数形式。式4和5将结果转换为极坐标方式后表示为:


有关DSP的文献中可以找到很多优化方法,可使上述DFT/FFT算法更小或更快。其中最重要的一种优化方法(可能也是最容易实现的)源于这样一个事实,那就是作为一个实数信号,其DFT幅度是相关于X(N / 2)对称的,因此:

编写FFT代码绝非易事。低功耗µC的一些局限又进一步使该任务复杂化。
存储器:我们所选的µC有2kB的RAM。已经知道该算法需要用到2N个16位变量来存储FFT数据,这样,我们的µC可以执行N最高为512的FFT。然而,固件的其他部分也要用到一些RAM。因此,在此项目中,我们限制N于256。若采用16位变量来表示每个值的实部和虚部,FFT数据总共需要1024字节的RAM。
速度:低功耗µC尽管具有高MIPS/mA性能,仍然需要一些优化手段来使运行FFT的指令数尽可能少。好在本应用所用的C编译器(IAR的Embedded Workbench for MAXQ,见www.iar.com)可提供多种级别的优化和设置。高效地使用硬件乘法器可使代码优化到可以接受的水平。
无浮点能力:所选的µC不具备浮点能力(低功耗产品一般都不具备浮点能力)。因此,所有运算都必须采用定点算法。为了表示小数,固件采用带符号的Q8.7表示法。这样,在固件中假定:
- 第0位至第6位代表小数部分
- 第7位至第14位代表整数部分
- 第15位代表符号位(二的补码)

所选的数据表示法还要适应FFT算法可能遇到的最大数值,同时又要提供足够的精度。例如,我们的ADC可提供带符号的8位采样,以二的补码表示。如果输入为最大幅度(对于带符号8位采样为127)的直流电压,则其能谱全部包含于X(0)中,用Q8.7表示为32512。这个数值能够由单个带符号的16位数据表示。
固件
以下部分讨论在低功耗µC上执行radix-2 FFT的固件实现。信号采样由ADC读出后被存储在x_n_re数组中。这个数组代表x(n)的实部。虚部存储在x_n_im数组中,在开始运行FFT前初始化为零。完成FFT后,计算结果取代原始采样数据,被存储在x_n_re和x_n_im中。获取采样
FFT算法假定采样是以固定的取样频率获得的。在为FFT获取采样时如果不加小心将会产生一些问题。例如,采样间隔的抖动就会给FFT结果引入误差,应尽力减小之。ADC采样循环中的判决语句会造成采样间隔的抖动。例如,我们的系统从ADC读取带符号的8位采样,并将其存储在一组16位变量中。在下面的程序清单1中给出了两种伪码算法,执行这种ADC读取-存储功能。算法1给出的方法会造成采样间隔的抖动,因为负采样比正采样需要更多的时间来读取并存储。
清单1. 两种ADC采样伪码算法。第二种算法避免了第一种的问题――采样间隔抖动。
// ALGORITHM 1: INCONSISTENT SAMPLING FREQUENCY - BAD!
// sample[] is an array of 16-bit variables
for i = 0 to (N-1)
begin
doADCSampleConversion() // Instruct ADC to sample Vin
sample[i] = read8BitSampleFromADC() // Read 8-bit sample from ADC
if (sample[i] & 0x0080) // If the 8-bit sample was negative
sample[i] = sample[i] + 0xFF00 // Make the 16-bit word negative
end
// ALGORITHM 2: FIXED SAMPLING FREQUENCY - GOOD!
// sample[] is an array of 16-bit variables
for i = 0 to (N-1)
begin
doADCSampleConversion() // Instruct ADC to sample Vin
sample[i] = read8BitSampleFromADC() // Read 8-bit sample from ADC
end
for i = 0 to (N-1)
begin
if (sample[i] & 0x0080) // If the 8-bit sample was negative
sample[i] = sample[i] + 0xFF00 // Make the 16-bit word negative
end
三角函数表
本FFT算法通过查表(LUT)而非计算得到正弦或余弦函数值。程序清单2给出了对于正弦和余弦LUT的申明。实际固件的注释中包含了自动生成这些LUT的源代码,可由程序调用。两个LUT均含有N / 2分量,因为旋转因子的索引号变化范围为从0至N / 2 - 1 (见图2)。清单2. 正弦和余弦函数LUT。
const int cosLUT[N/2] = {+128,+127,+127, ... ,-127,-127,-127};
const int sinLUT[N/2] = {+0 ,+3 , +6, ... ,+9 , +6, +3};
这些LUT中的数组被声明为const,强制编译器将它们存储于代码空间而非数据空间。由于LUT数值须采用Q8.7表示法,它们由正弦和余弦的实际值乘以27后得到。
位反转
位反转排序(N已知)可在运行时通过计算、查表或直接利用展开循环编写。所有这些方法都需要在源代码的尺寸和运行速度间进行折衷。本FFT应用利用展开循环进行位反转,其源代码较长,但运行速度快。程序清单3显示了该展开循环的实现。本应用固件的注释中包含了用于程序自动生成展开循环的源代码。清单3. 用于实现N = 256的位反转的展开循环。
i=x_n_re[ 1]; x_n_re[ 1]=x_n_re[128]; x_n_re[128]=i; i=x_n_re[ 2]; x_n_re[ 2]=x_n_re[ 64]; x_n_re[ 64]=i; i=x_n_re[ 3]; x_n_re[ 3]=x_n_re[192]; x_n_re[192]=i; i=x_n_re[ 4]; x_n_re[ 4]=x_n_re[ 32]; x_n_re[ 32]=i; ... i=x_n_re[207]; x_n_re[207]=x_n_re[243]; x_n_re[243]=i; i=x_n_re[215]; x_n_re[215]=x_n_re[235]; x_n_re[235]=i; i=x_n_re[223]; x_n_re[223]=x_n_re[251]; x_n_re[251]=i; i=x_n_re[239]; x_n_re[239]=x_n_re[247]; x_n_re[247]=i;
Radix-2 FFT算法
采样按照位反转方式重新排序后就可进行FFT运算了。本radix-2 FFT应用的固件通过三个主循环执行图2所示的蝶型运算。外循环计数log2(N)级FFT运算。内循环执行每一级的蝶型运算。FFT算法的核心部分是执行蝶型运算的一小块代码。程序清单4给出了这一块代码,遗憾的是,它是本应用中唯一“不可移植”的固件。宏MUL_1和MUL_2利用µC的硬件乘法器执行单指令周期乘法运算。这些宏的内容专用于MAXQ2000,可在实际固件中全部看到。
清单4. 用C编写的蝶型运算。
/* (1) Macro MUL_1(A,B,C): C=A*B (result in Q8.7)*/
/* (2) Macro MUL_2(A,C) : C=A*last_B (result in Q8.7)*/
MUL_1(cosLUT[tf],x_n_re[b],resultMulReCos);
MUL_2(sinLUT[tf],resultMulReSin);
MUL_1(cosLUT[tf],x_n_im[b],resultMulImCos);
MUL_2(sinLUT[tf],resultMulImSin);
x_n_re[b] = x_n_re[a]-resultMulReCos+resultMulImSin;
x_n_im[b] = x_n_im[a]-resultMulReSin-resultMulImCos;
x_n_re[a] = x_n_re[a]+resultMulReCos-resultMulImSin;
x_n_im[a] = x_n_im[a]+resultMulReSin+resultMulImCos;
复数的极坐标转换
为了便于确定VIN频谱的幅度,我们须要将复数形式的X(k)转换为极坐标形式。实现该转换的固件示于程序清单5。幅度值取代了原始的FFT结果,因为固件不再需要这些数据。清单5. FFT结果从复数形式转换为极坐标形式。
const unsigned char magnLUT[16][16] =
{
{0x00,0x10,0x20, ... ,0xd0,0xe0,0xf0},
{0x10,0x16,0x23, ... ,0xd0,0xe0,0xf0},
...
{0xe0,0xe0,0xe2, ... ,0xff,0xff,0xff},
{0xf0,0xf0,0xf2, ... ,0xff,0xff,0xff}
};
...
...
/* Compute x_n_re=abs(x_n_re) and x_n_im=abs(x_n_im) */
...
...
x_n_re[0] = magnLUT[x_n_re[0]>>11][0];
for(i=1; i>11][x_n_im[i]>>11];
x_n_re[N_DIV_2] = magnLUT[x_n_re[N_DIV_2]>>11][0];
频谱幅度并非根据式4计算得到,而是通过一个二维LUT查表得到。第一索引为频谱实部的高4位(MSB),第二索引为频谱虚部的高4位。为得到这些数据,可将带符号的16位数据右移11次。在从频谱的实部和虚部取得索引号前,需首先将它们转换为绝对值。因此,符号位为零。从式6我们已经知道,频谱的幅度是关于X(N / 2)对称的,因此我们只需将前(N / 2) + 1个频谱数据转换为极坐标形式。还有,我们可以看到,对于实数输入采样,X(0)和X(N / 2)的虚部总为零。因此这两条谱线的幅度被单独计算。本项目实际固件的注释中包含了用于自动生成该LUT的源代码,可由程序调用来计算X(k)的幅度。
Hamming或Hann窗
此项目固件还包括了对输入采样加Hamming或Hann窗的LUT (Q8.7格式)。加窗函数可有效降低对时域采样x(n)的舍入操作所引起的频谱泄漏。Hamming和Hann窗函数分别如式7和8所示。

程序清单6给出了实现这些函数的代码。同样,本项目实际固件的注释中包含了用于自动生成这些LUT的源代码,可由程序调用来实现这些窗函数。
清单6. 用来实现Hamming和Hann窗函数的LUT。
const char hammingLUT[N] = {+10, +10, +10, ... ,+10, +10, +10};
const char hannLUT[N] = { +0, +0, +0, ... , +0, +0, +0};
...
...
for(i=0; i<256; i++)
{
#ifdef WINDOWING_HAMMING
MUL_1(x_n_re[i],hammingLUT[i],x_n_re[i]); // x(n)*=hamming(n);
#endif
#ifdef WINDOWING_HANN
MUL_1(x_n_re[i],hannLUT[i]),x_n_re[i]); // x(n)*=hann(n);
#endif
}
测试结果
为了测试该FFT应用的性能,固件将X(k)幅度通过µC的UART端口上传给PC。专门编写的FFT Graph软件(随该项目固件一起提供)用于从PC串口读取这些幅值,并以图形方式实时显示频谱。图3显示了µC以200ksps采样四种不同输入信号并处理后,由FFT Graph所显示出来的结果:- 4.3V直流信号
- 50kHz正弦信号
- 70kHz正弦信号
- 6.25kHz方波

图3. FFT Graph软件显示的由低功耗µC计算出的频谱。
接下来干什么?
有兴趣的读者还可以花费大量的时间来继续优化和重新配置该FFT应用。尽管在本文中我们选择了radix-2算法,还有很多其他算法可以显著降低加法和乘法运算量。很多本文所未提及的优化可以提升FFT的速度。例如,作为纯实数的输入采样,其虚部总为零,频谱中只有前半部分有实际意义。利用这一点,第一级和最后一级FFT的执行速度可进一步优化,但需要付出更多的程序空间。总之,本文所讨论的算法对于低功耗µC上的FFT应用而言,提供了一个很好的出发点。如果想了解更多信息和具体实现的细节,请查阅我们为本应用所提供的、带有详细注释的固件信息。
参考文献
Cooley, J. W.和J. W. Tukey, An Algorithm for the Machine Computation of Complex Fourier Series, Mathematics Computation, 第19期,第297-301页,1965。Lemieux, Joe, Fixed-point math in C, Embedded Systems Programming, 2003年10月。
Proakis, John G.和Dimitris G. Manolakism, Digital Signal Processing Principles, Algorithms, and Applications, 第3版, Prentice Hall, 1996。
Smith, Steven W., The Scientist and Engineer's Guide to Digital Signal Processing, 第2版, California Technical Publishing, 1999。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
超低功耗微控制器单元(MCU)主要有哪些应用?2021-06-17 2581
-
ADuCM4050超低功耗微控制器2021-05-13 921
-
微控制器功耗管理模式:降低功耗的方式2020-02-06 5594
-
选择低功耗微控制器开发,避免资源受限规则2019-12-27 3156
-
基于微控制器的选择解读超低功耗意义2019-07-22 1897
-
低功耗微控制器MSP430的应用2017-10-12 925
-
基于LPC1100微控制器的低功耗特性2017-09-26 776
-
什么是低功耗微控制器?2017-07-24 991
-
低功耗智能电源应用的微控制器2017-06-30 869
-
ROHM旗下LAPIS Semiconductor开发出低功耗微控制器2016-01-13 1629
-
利用低功耗微控制器开发FFT应用2009-04-23 451
-
低功耗模式下微控制器时钟配置应用2009-04-22 431
全部0条评论

快来发表一下你的评论吧 !

