

一阶LC电路的仿真设计案例
模拟技术
描述
LC谐振电路具有选频功能,广泛用于各种通信电路。本文就一阶LC电路进行仿真,以此来进一步加深对电路特性的理解和记忆。
谐振
当电路中存在感性元件(如电感)或者容性元件(电容)时,信号源(比如电流源)的频率变化会使得电路总体呈现容性、感性或者电阻性。当电路呈现电阻性时,就说该电路发生了谐振。最简单的谐振电路就是一阶LC谐振电路,只由一个电感、一个电容和信号源组成。
并联谐振电路
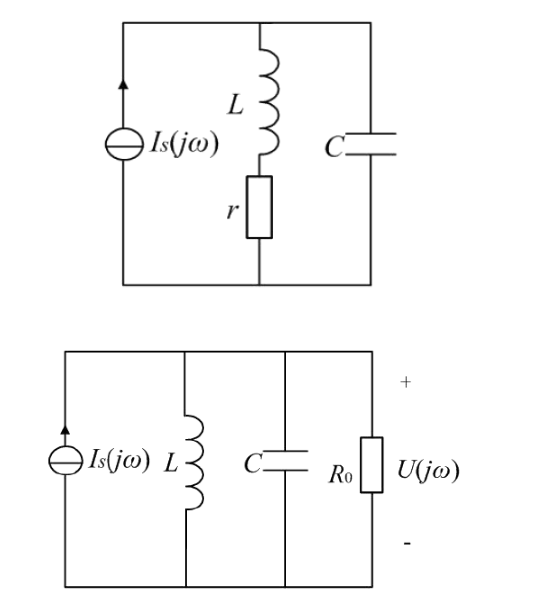
一阶并联型LC谐振电路如上面左图所示,其中的电阻r是电感的固有损耗,这个固有损耗值一般非常小(以至于理想状态下可以完全忽略),但是一般进行谐振分析时都把它考虑在内。通常将该网络等效变换到上面的右图形式。这个电路有以下几个重要参数:
1、谐振条件$\omega C = \frac{1}{\omega L}$,满足该条件的谐振角频率$\omega_0 = \frac{1}{\sqrt{L C}}$,谐振频率$f_0=\frac {\omega_0} {2 \pi} $;
1、等效电阻$R(\omega)=\frac{(\omega L)^2}{r}$;
2、发生谐振时,$R(\omega)$记为谐振电阻$R_0$,$R_0=\frac{(\omega_0 L)^2}{r}$;
3、品质因数$Q_0=\frac{R_0}{\omega_0 L}=R_0 \omega_0 C$;
4、通频带$B_0.7=\frac{f_0}{Q_0}$;
串联谐振电路
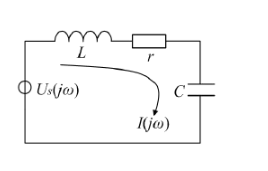
串联谐振电路的很多公式跟并联是相似的,有些特性与并联也是对应的。串联回路的分析要简单很多,可以很容易写出阻抗表达式。而且也不用进行等效变换,该电路的一些公式结论如下:
1、谐振条件为$\omega L = \frac{1}{\omega C}$,谐振角频率不变,仍然是$\omega_0 = \frac{1}{\sqrt{L C}}$,谐振频率$f_0=\frac {\omega_0} {2 \pi} $。
2、因为电阻r直接作为了阻抗的实部,因此谐振电阻$R_0=r$。
3、品质因数是并联的倒数,$Q_0=\frac{\omega_0 L}{R_0}=\frac{1}{R_0 \omega_0 C}$。
4、通频带$B_0.7=\frac{f_0}{Q_0}$;
谐振电路仿真
以并联电路为例,在PSpice中连接好最基本的电路,电路参数在图中已经标明。根据第一节的结论公式和该并联电路器件参数,我们可以计算出电路的谐振角频率、谐振频率、谐振电阻、品质因素分别为:$\omega_0=25M rad/s$、$f_0 \approx 3.9789MHz$、$R_0=100 \Omega$、$Q_0=100$。
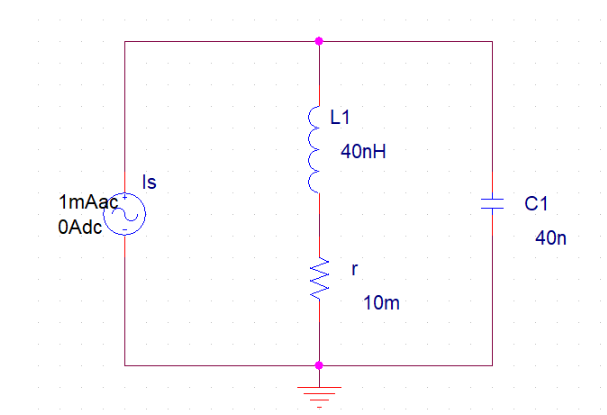
阻抗特性
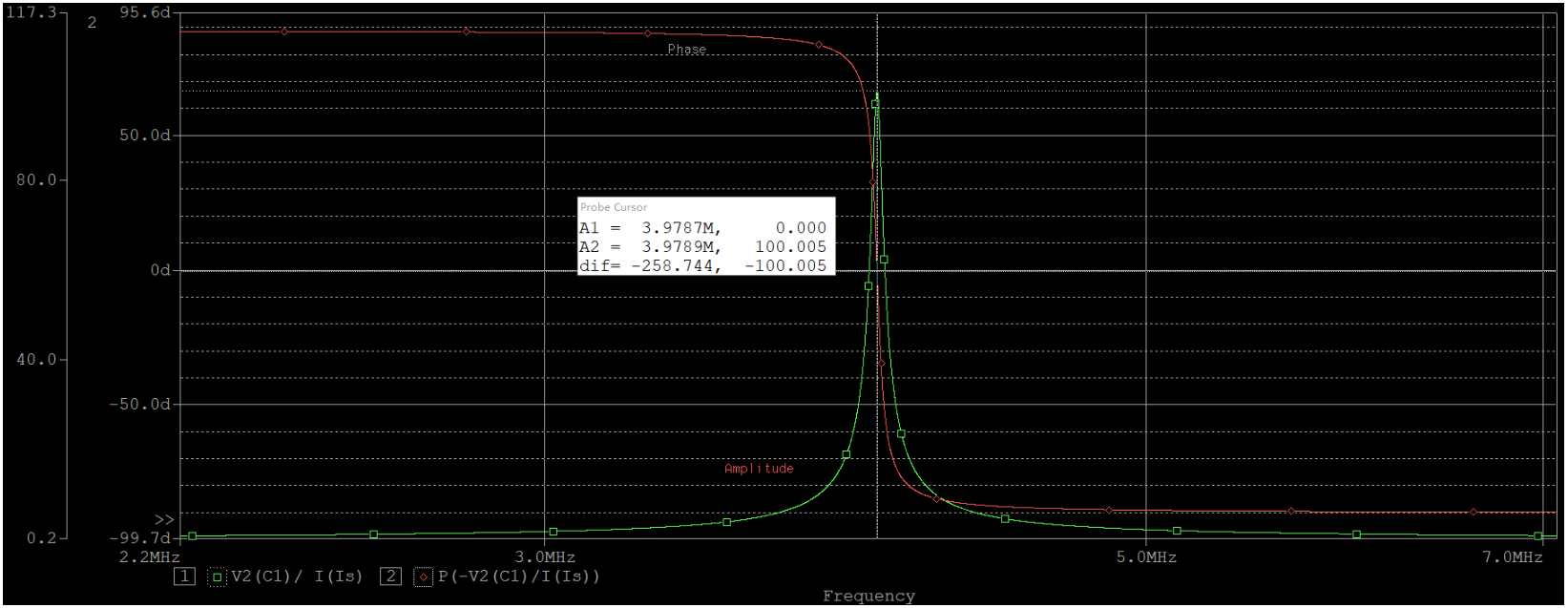
上图是电路总阻抗的幅频(绿线)和相频(红线)特性曲线。先来看相频,当$f《3.9787MHz$时,相位角为正,说明电路呈感性;当$f》3.9787MHz$时,相位角为负,所以电路呈容性;而$f=3.9787MHz$时,电路呈电阻性,这说明此时电路谐振,实际测得的谐振频率$f_0=3.9787MHz$。这个频率值很接近我们计算所得的理论值。
我在仿真的时候,将每十倍频的采样点数故意设得非常高,也就是说结果的精确度等级几乎可以达到0.0001。之所以强调这一点,是希望读者注意到上面谐振频率的误差,即$0.0002MHz$,并非是由于软件仿真导致的,而是我们的理论值出错了。谐振角频率$\omega_0 = \frac{1}{\sqrt{L C}}$成立的前提条件是$\omega_0 L 》》 r$,也就是公式中其实忽略了小r的影响,而真正零误差的公式为$\omega_0 = \sqrt{ \frac{1}{L C} -\frac{r^2}{L^2} }$,用该公式计算出来的谐振频率恰好就是图中的$3.9787MHz$。当然,实际中基本都忽略r的影响,因为性能好的电路中,其影响真的是微不足道啊。
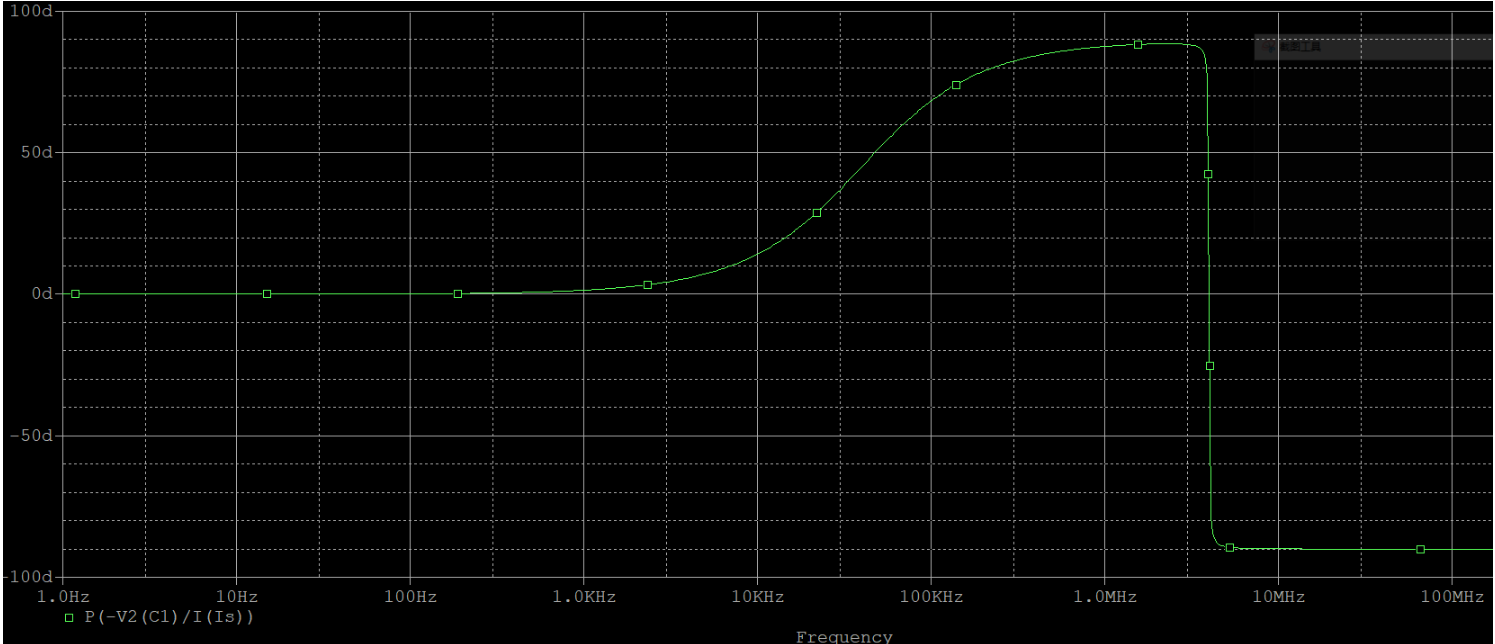
对于相频曲线,还要关注的就是变化规律。如上图所示,可以看到在谐振频率附近,曲线的斜率非常大,变化得非常快。这说明,谐振点是个非常不稳定的点,很容易偏移到感性区域或者是容性区域,在实物电路的调节中相信这个问题会相当明显并且棘手。此外,我们刚讲过r对相频的影响,这个再次体现在了低频区域的相位上,大约在1MHz以下,相位就开始回零,最终趋于纯电阻性。其原因可以通过阻抗或者导纳公式推知,由于是低频段分析,因此过程中可将${(\omega L)}^2$忽略简化分析:
$Y(j\omega) = j\omega C + \frac{1}{j\omega L + r}=\frac{r}{r^2 + (\omega L)^2}+j[\omega C - \frac{\omega L}{r^2 + (\omega L)^2}] $
$When \; \omega L 《《 r ,Y(j\omega) = \frac{1}{r}+j[\omega C - \frac{\omega L}{r^2}]$
$\Theta (j\omega) = \arctan \omega (rC-\frac{L}{r})$
再看第一张图中的幅频,曲线呈尖峰状。结合相频曲线,可知在电路谐振时(是忽略r时的谐振,而非电路实际真正的谐振),阻抗的幅值达到最大,为$100 \Omega$。这里的$100 \Omega$恰好就是谐振电阻$R_0$。
以上是并联电路的阻抗特性,在串联电路中,阻抗特性曲线如下图所示,刚好和并联相反。
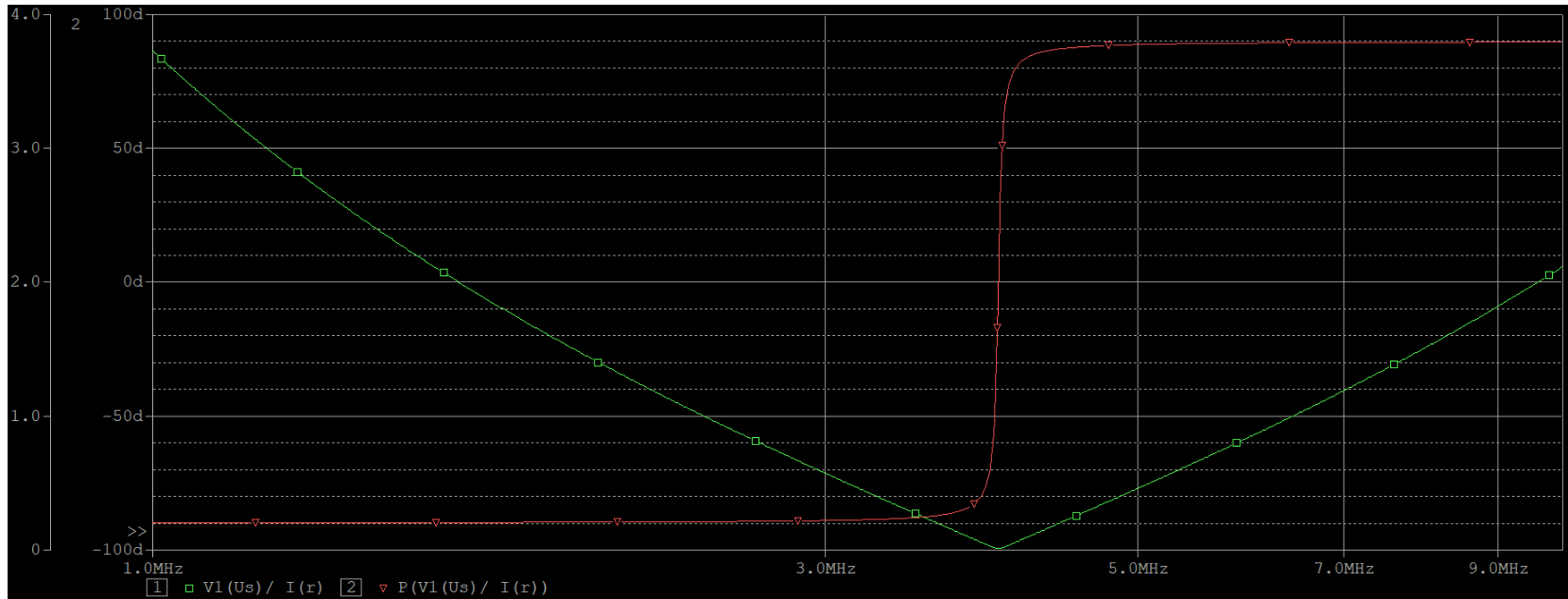
选频特性和通频带
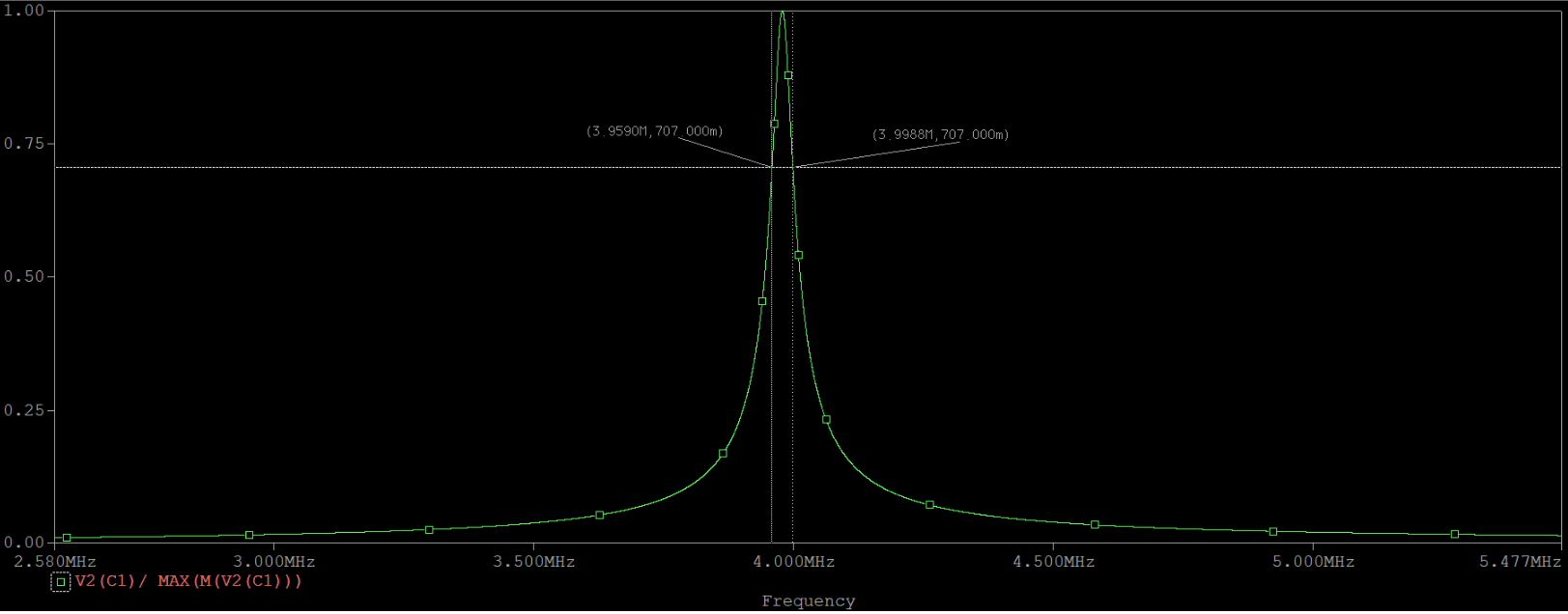
上图是回路电压的归一化曲线,可以表示为$\frac{U(j\omega)}{U_0}$,通过一定变换,可知它与$\frac{Z(j\omega)}{R_0}$是等价的。直观地说,上图就是阻抗幅频曲线归一化后的样子,并且$\frac{U(j\omega)}{U_0}$的相频与阻抗相频特性是完全一样的。
这里,可以测得通频带大约为$39kHz$,允许通过的频率范围就是$3.959MHz$到$3.999Mhz$。结合理论公式,我们知道:通频带和选频特性是矛盾的,因为选频特性越好,要求品质因数要越大;如果通频带越大,则品质因数就要变小。所以,电路设计中要综合权衡这两个指标。
串联电路的选频特性曲线和并联的一样,也是呈尖峰状,只不过用于衡量选频能力的公式变为$\frac{I(j\omega)}{I_0}$。
谐振电路设计
并联电路
一阶LC谐振电路需要设计的参数无非就是电感L值和电容C值,而固有损耗通常都是客观决定的。L、C值的选择会影响电路的谐振频率、谐振电阻、品质因数等特性。以并联电路为例,下面讨论参数的选择问题。
首先,很明显的一点是,$L·C$的值越小,谐振频率越大;而且假设L、C各自减小到原来的一半,那么谐振频率只增大两倍,而不是四倍。
第二个是谐振电阻,将原来的公式进行变换可得$R_0=\frac{L}{C·r}$,由此可知L越大,C越小,那么谐振电阻就越大;而且如果L增大到原来的两倍,C减小到原来的一半,那么谐振频率仍然不变,但是谐振电阻却增大了四倍。
品质因数跟谐振电阻有很大关系,将公式进行变换可得$Q_0=\sqrt{\frac{R_0}{r}}$,也就是说如果谐振电阻能够增大到4倍,那么品质因数可以增大到2倍。
并联回路的最大电压就是谐振时候的电压,该电压值$U_0=I_{sm}·R_0$,它的增大趋势和谐振电阻相同。
此外,我们必须要注意电感和电容的耐压耐流特性。在并联电路里,谐振时候流过电感和电容的电流幅值最大,并且满足$|I_{C0}|=|I_{L0}|=Q_0|I_{sm}|$。其增大趋势是和品质因数相同。
串联电路
与并联一样,$L·C$的值越小,谐振频率越大;而且假设L、C各自减小到原来的一半,那么谐振频率增大两倍。
谐振电阻取决于固有损耗值。
品质因数$Q_0=\sqrt{\frac{LC}{r^2}}$,L增大,C减小,可以增大品质因数。
串联回路的最大电流就是谐振时候的电流,该电流值$I_0=\frac{U_{sm}}{R_0}$,与谐振电阻呈反比。
在串联电路里,谐振时候电感和电容的分压最大,并且满足$|U_{C0}|=|U_{L0}|=Q_0|U_{sm}|$。其增大趋势是和品质因数相同。
固有损耗对电路的影响
最后想要说明的一点就是固有损耗带来的影响。因为仿真软件里的模型一般都是理想的,也很难说固有损耗一般在哪个范围。我尝试了不同大小的固有损耗值,发现它对电路的影响还是比较有趣的。
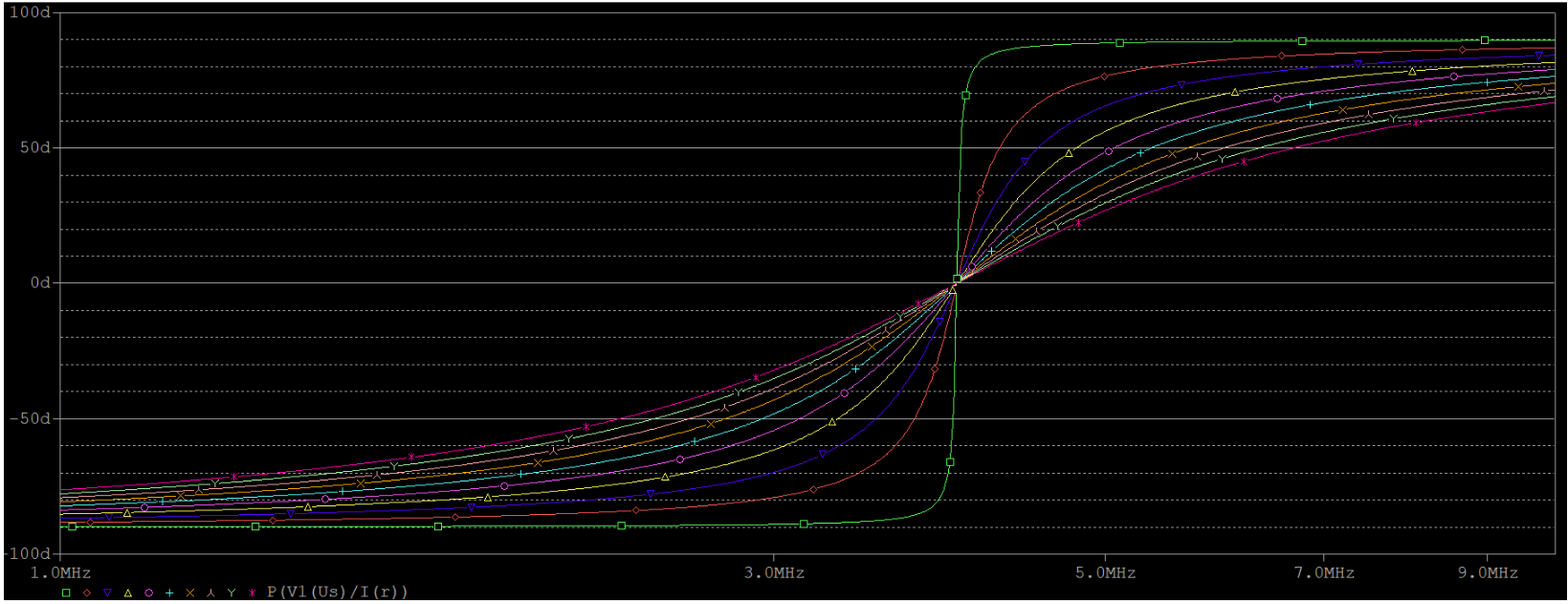
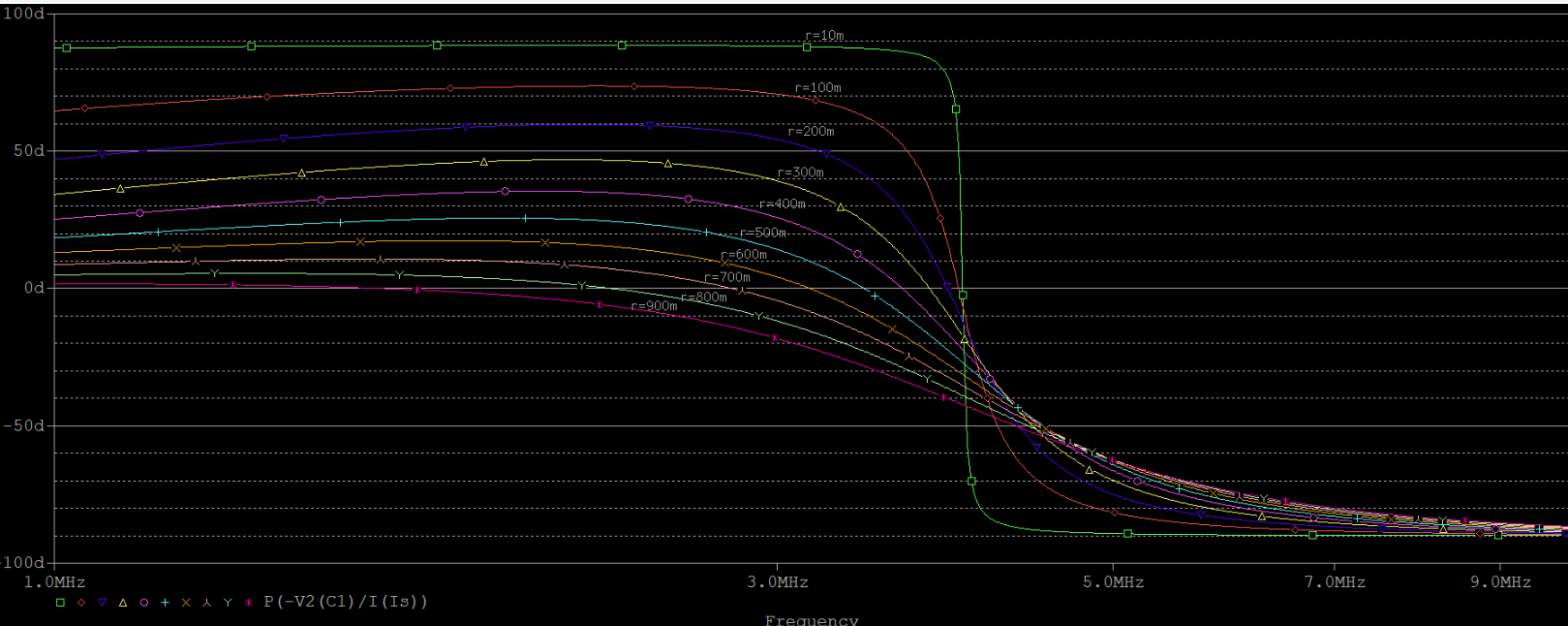
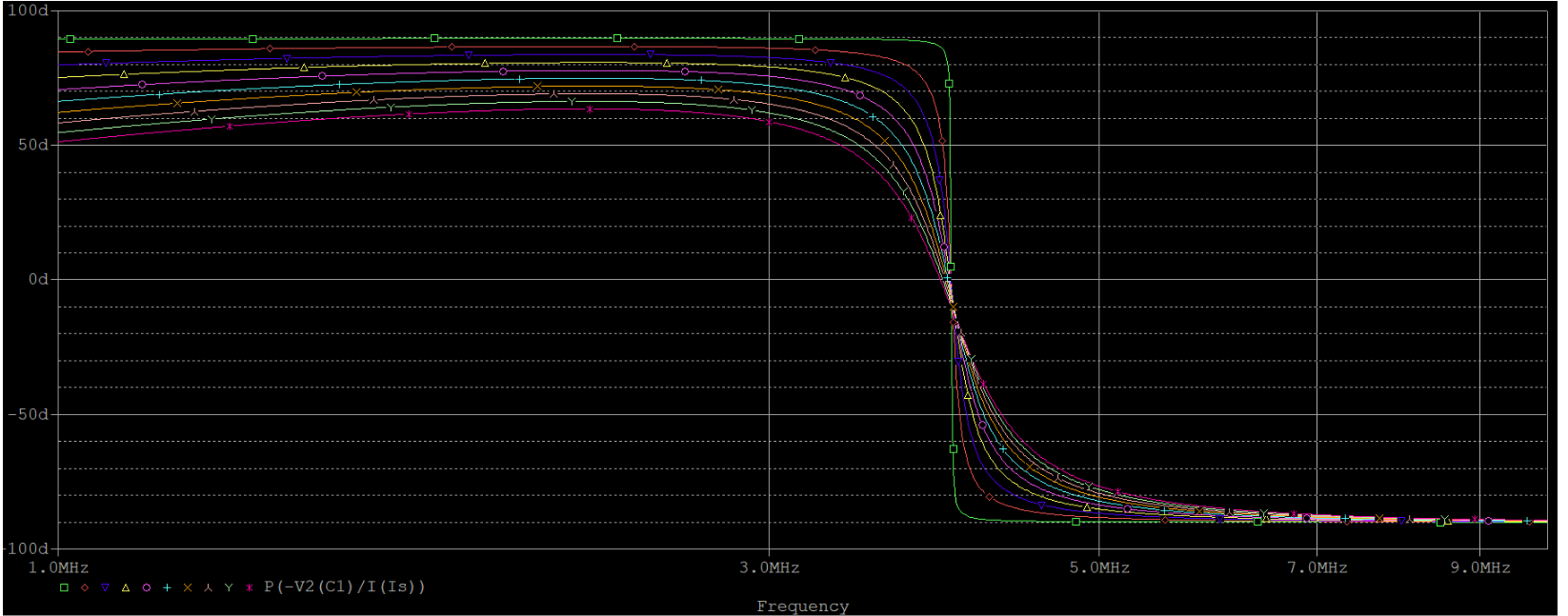
关于固有损耗对谐振频率的影响,并联和串联电路表现得截然不同。串联电路的谐振频率丝毫不受干扰(上第一幅图),并联(上第二幅图)的在上文就已经提到过了。我们看到,固有损耗从$10m \Omega$仅仅变到$900m \Omega$,谐振频率就偏移了将近50%。解决这一问题的方法,就是一定范围内增大L,从而保证$\omega_0 L 》》 r$这一前提条件。例如,就之前的仿真电路,将电感L调整为$200nH$,电感调整为$8nF$,此时谐振频率仍然不变,但是对固有损耗的抵抗力显然增强,如下图所示(r的取值同上面):
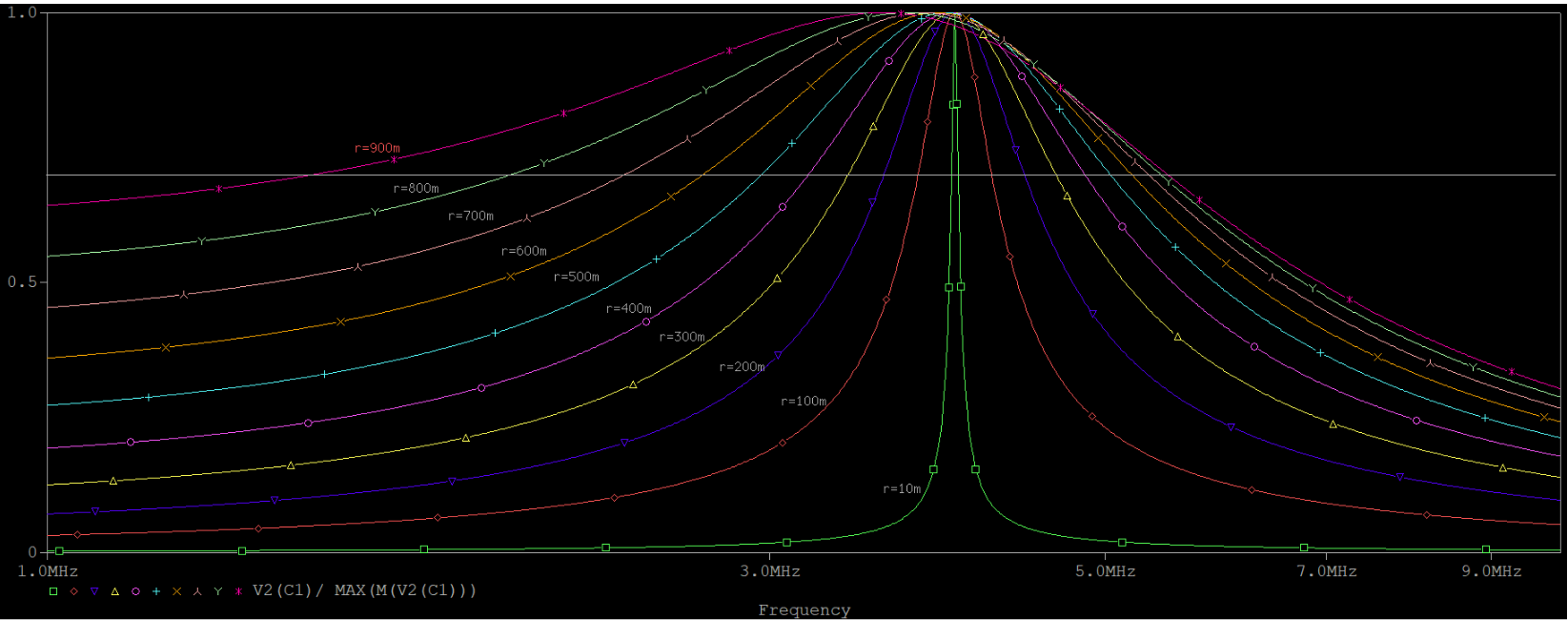
谐振电路最重要的特性除了谐振频率,还有就是选频特性或者说通频带。比较遗憾的是,同谐振频率一样,固有损耗对选频特性的影响也非常大。如下图所示,通频带的增大非常明显,与之相反,我们可以观察到波峰的位置偏移程度较小,也就是说电压中心频率对r是不太敏感的。该问题的解决方法与谐振频率一样。
除了谐振频率和选频特性,下面分析了其他特性的变化,这些变化的前提是$\omega_0 L 》》 r$。
谐振电阻方面,串联电路中谐振电阻就是固有损耗电阻,因此r越大,$R_0$也越大;并联电路中,$R_0=\frac{L}{C·r}$,所以$R_0$与r呈反比关系。
品质因数公式在串联和并联中互为倒数,但其实可以化成相同的形式:$Q_0=\sqrt{\frac{R_0}{r}}$。因此,品质因数也与r呈反比关系。
带载LC谐振电路
以上的所有分析都是针对空载电路来说的,然而实际电路中,都是带载的情况,此时为了获得更好的选频能力,该如何选择L和C的值呢?
我们假设电感的固有损耗为$r$,负载电阻为$R_L$,则$Q_L=\frac{R_L//r}{\omega_0 L}=\frac{1}{rk+\frac{1}{R_Lk}}$,$k=\sqrt{\frac{C}{L}}$。如果要使品质因数最大,则要满足$k^2=\frac{C}{L}=\frac{1}{R_Lr}$。进而,假设认为电感是理想的,没有损耗,那么回路电阻完全取决于负载,此时$Q_L=\sqrt{\frac{C}{L}}R_{\Sigma}$,则C越大L越小,品质因数越大,选频特性越好。
-
一阶电路的三要素法 一阶电路等效电阻怎么求?2023-10-22 7748
-
一阶电路与二阶电路的时域分析2023-03-02 13664
-
一阶电路的动态响应(2)2022-08-08 665
-
一阶电路的实验指导书资料说明2020-05-26 1271
-
一阶电路和二阶电路的时域分析详细资料概述免费下载2018-07-25 1593
-
电路设计--一阶电路2017-08-07 2172
-
一阶有源低通滤波电路与最经典一阶低通滤波器电路图2017-07-24 183645
-
一阶电路的零输入响应2009-07-27 7892
-
一阶RC电路的暂态响应2008-12-17 1861
-
一阶电路的响应2008-12-11 2306
-
一阶电路的响应测试2008-11-02 11807
-
一阶动态电路的动态过程2008-09-25 10563
-
RC一阶电路的响应测试2008-09-24 75971
全部0条评论

快来发表一下你的评论吧 !

