s域传递函数与一阶低通滤波器行为之间的关系

　　最近，我一直在写关于滤波器的主题，虽然我一直专注于实际应用考虑，但我觉得有必要解释一些重要的理论概念，以便那些想要更彻底的人受益理解并分析模拟滤波器的行为。现在每个人都可以使用软件工具，使复杂的滤波器设计相对轻松，但我认为完全忽略数学基础并不是明智的，虽然它对完成许多现实设计任务不是绝对必要的。

　　s域

　　滤波器的响应可以用s域传递函数表示;变量s来自拉普拉斯变换，代表复频率响应。例如：

　　

　　该传递函数是一阶低通滤波器的频域特性的数学描述。s域表达式有效地传达了一般特征，如果我们想要计算特定的幅度和相位信息，我们所要做的就是用jω代替s，然后在给定的角频率下评估表达式。

　　您可能想知道K和ωO来自哪里-您可能从未见过具有以K和ωO表示的元件值的电路图。这里的想法是K和ωO就像模板的一部分，在下一节中我们将看看该模板和电路图之间的关系。

　　s域的电路分析

　　RC低通滤波器是与频率相关的分压器。在s域分析中，电阻器的阻抗为R，电容器的阻抗为1/（sC），如下图所示：

　　

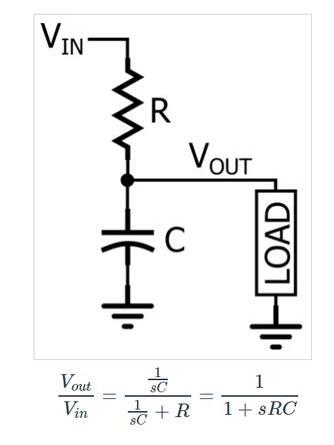
　　s域与电路分析

　　如果我们将这个表达式与标准化传递函数进行比较，我们可以看出K=1且ωO=1/RC。一旦你知道K和ωO代表什么，使用标准化形式的便利性就变得清晰了：K是电路在DC上的增益，ωO是截止频率。因此，通过将电路的传递函数与标准化传递函数进行比较，可以立即为一阶低通滤波器的两个特征定义表达式，即DC增益和截止频率。

　　另一种标准形式的一阶低通传递函数如下的方程所示：

　　

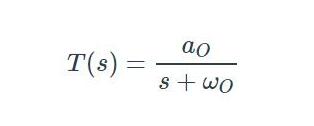
　　如果我们将上面方程的分子和分母除以RC，我们可以将电路的传递函数拟合到下面的这个模板中：

　　

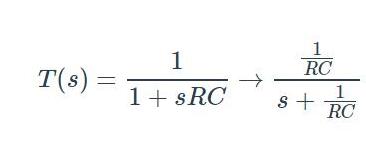
　　因此，aO=1/RC，ωO=1/RC。这种形式并没有直接给我们DC增益，但如果我们评估s=0的标准化表达式，我们就有了：

　　

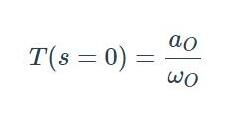
　　这意味着我们的RC滤波器的DC增益为（1/RC）/（1/RC）=1，DC的单位增益正是我们对无源低通滤波器的期望。

　　理解截止频率

　　我们已经看到标准传递函数中的ωO代表截止频率，但这个事实的数学基础是什么？

　　首先，让我们将标准的s域传递函数转换为等效的jω传递函数。

　　

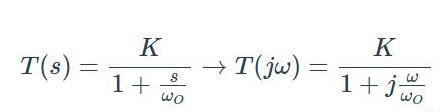
　　现在让我们评估截止频率的表达式：

　　

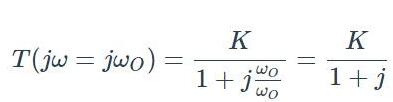
　　分母是一个复数，因此幅度可以表示为：

　　

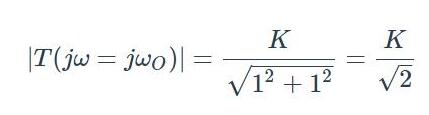
　　由于K是DC增益，幅度为1伏的极低频率输入信号将导致幅度为K伏的输出信号。如果输入频率增加到每秒ωO弧度，输出幅度将为：

　　上式中：

　　因子代表的是对应于-3dB，您可能知道，截止频率的另一个名称是-3dB频率：

　　

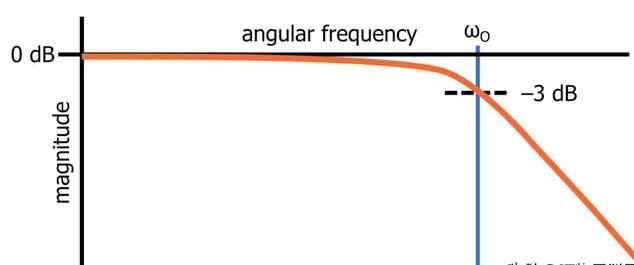
　　上图是一阶无源低通滤波器的幅度响应的形状，当它被绘制为以dB为单位的幅度与对数频率的关系。

　　这种直接的传递函数分析清楚地证明了截止频率只是滤波器幅度响应相对于极低频幅度响应降低3dB的频率。

　　截止频率和相移

　　低通滤波器的截止频率对于电路的相位响应也具有特殊意义。如果我们以x+jy的形式写出一个复数，我们就可以按如下方式计算出相位：

　　

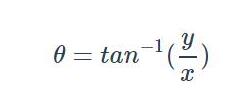
　　因此，我们的RC低通滤波器的整体相位响应是：

　　

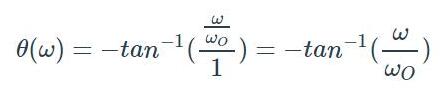
　　如果我们在ω=ωO处评估该表达式，则其相移为：

　　

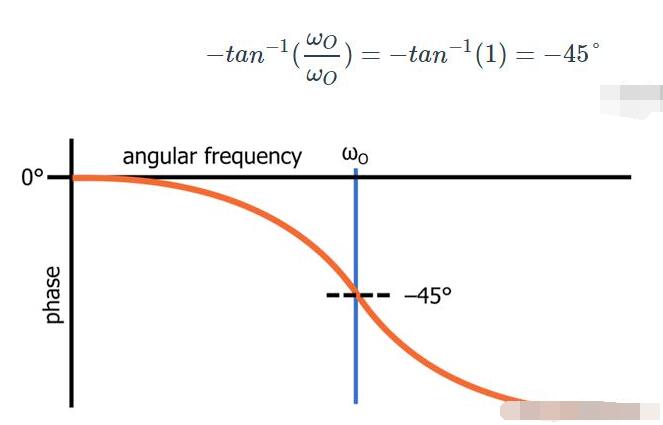
　　上图是当相移相对于对数频率绘制时一阶无源低通滤波器的相位响应的形状。

　　由一阶低通滤波器产生的最大相移为90°，因此该分析告诉我们截止频率是电路相位响应的“中心”-换句话说，它是滤波器产生一半的最大相移的频率。

　　结论

　　我希望您对s-domain（S-域）概念和传递函数分析的这一简要介绍很感兴趣。模拟滤波器电路的数学基础起初可能有点令人生畏，但我认为值得您花些时间来熟悉这些课题。我将在以后的文章中继续探讨这个课题，敬请关注！