

利用低价位数字测试仪器对高速时钟进行有效测试
测量仪表
描述
当你需要测量高速时钟频率时,可能选择价位昂贵的台面仪器。而实际上,使用低价位数字测试仪器的数字捕获能力,再加上一些DSP软件函数即可测试高速时钟。下文介绍了具体的实现办法。
奈奎斯特定律的混叠
我们都相信,取样原理称,取样频率必须比被测最高频率高两倍。例如,当捕获160MHz的时钟,就要用320MHz以上的频率。如果使用33.333MHz取样器捕捉160MHz时钟,例如NextestMarerick公司的数字捕捉仪,则时钟信号必然会出现混叠,或者可能得到另一个较低的频率。
一个160MHz时钟会混叠成为6.666MHz,因为160MHz正好比33.333MHz*5=166.666MHz低6.666MHz。用33.3333333MHz的取样率对160MHz取样时,在频域产生的不同频段如图1a所示。图中最右边是133MHz频段(4*33MHz)至166MHz频段(5*33MHz)。类似DCI那样的仪器不允许你真正测得该频段的信号,但是这些信号时的确存在的,并且证明这是落入到奈奎斯特频率段的混叠频率。图中黄色表示的是从DC至16.666MHz。
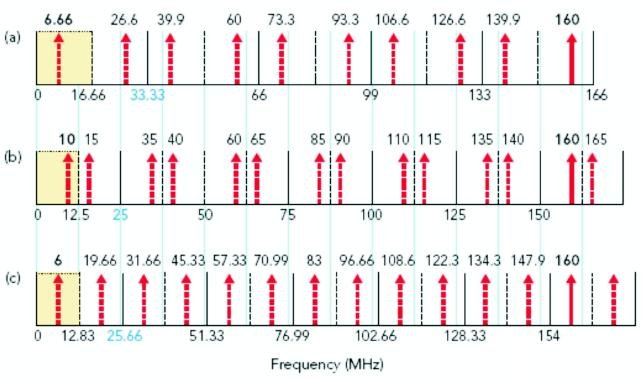
图1对160MHz信号取样,a)用33MHz采样率,b)用25MHz产生不定性,c)用正交采样率排除不定性
因为160MHz正好落在比166.666MHz低6.666MHz的位置上,它将通过几个频段向后混叠(而你同样不能直接观察到它),由红色箭头表示。实际上你能够看到的6.666MHz混叠会出现在奈奎斯特频段内,混叠出现在DC以上6.666MHz的原因是,它来自约为取样率4.5倍的上半部频段,再折叠回来表现为镜子里的反向图像。相位也会反转,但是对采样目的来说,相位并不重要。
现在你能够看到在奈奎斯特频段内的6.666MHz,但这是否表明了你已经捕获到了160MHz呢?并非如此。如果你在奈奎斯特频段真正看到6.666MHz,则它可能是160MHz,也可能是其他在图1a上不列出的频率之一(26.6、39.9、60、73.3等等)。一旦确实证明是在奈奎斯特频段内的6.666MHz,则这就是捕捉到的160MHz,而且还需要使用不同的取样率进行再抽样。
如果使用另一个与原来33.333MHz不同的取样率对160MHz时钟取样时,混叠频率降落在不同的位置。如果你见到混叠频率再次落在160MHz,则似乎两次取样都可以补到160MHz了,可以排除其他频率的可能性。因此,新取样率不能太靠近原来的取样率,不然它们就会因为拥有公共因子而被删除,并且落到比160MHz较低的频率上。录入,你再用25MHz取样频率对160MHz取样时,真正的结果并不很明显(图1b)。
用25MHz取样表明,160MHz比150MHz(5*25)高10MHz。故混叠频率会回到奈奎斯特频段内比DC高10MHz的地方。不幸的是,由于33.333MHz(30ns)和25MHz(40ns)具有公共因子1/10ns,或者100MHz,所以它们最后将产生共同的混叠频率。
使用正交取样频率
因为第二个取样频率将确认真正捕捉的信号,因此需要一个完全与原来取样频率无关的频率(没有公共因子)来进行取样。一种方法是采用锁相环使系统时钟偏移,但这样会导致标准系统时钟周期分辨率的变化。
对于NextestMaverick的仪器,可以使用APG的锁相环来选择频率。所以你必须挑选少数几个与33.333MHz取样频率没有公共因子的频率,例如77MHz(12.987013ns),周期采用38.961039ns(3*系统时钟周期),相应取样频率是25.666666MHz。可是,不能在运行中切换锁相环,因此必须做一次捕捉时全部时间复位,然后再做第二次捕捉。因为捕捉时间极快,对测试时间影响不大。
采用这个取样率获得的混叠频率如图1c所示。图中160MHz准确地落在比154MHz(6*25.66MHz)高6MHz的地方,是混叠频率出现在奈奎斯特频段内。注意25.66MHz取样的全列混叠频率与33.333MHz取样的全列混叠频率完全不相同。这正是本文所介绍的技术工作的重点。可再次通过图1a来证实这一要点。图中出正确结果160MHz以外,在两列混叠中没有出现相同的频率。
需要记住的是,要设置两次不同的时间、两个不同的数组和两种不同功能的脉冲组合。不要试图在运行中切换定时设置,因为大部分测试仪器不支持在运行期间切换时间。
还需要设定捕捉一起去捕捉时钟引脚,以期收集到表示时钟引脚瞬变的数码1和0序列。显然,比较器电压要设定在时钟50%的点上,如果引脚需要端接,则还需要接入有源负载。
一旦功能测试过程完成捕捉运作,则立即将截取的数据转换为波形。此外,从波形减去0.5,使得捕捉的1表示为电压0.5,而捕捉的0表示电压-0.5。
确认波形的X标度要设定为实际捕捉的取样率,否则就不能获得正确的结果。有些测试仪器可以自动做到这些,有些则不能,因为它们并非设计用于时间波形的捕捉。
确定时钟频率
现在对两个在不同取样率下捕捉到的波形计算波形的瞬变数,然后出去UTP(单位测试周期),这个方法还未曾被运用。
波形可能会有少量“低矮瞬变”,即由噪声产生的接近比较器阀值的特殊边沿,这种特殊瞬变可导致测试错误地估计时钟频率,引起读数错误。一种将时域数据转换成频率数据的方法是FFT。FFT把低矮瞬变作为噪声处理,而不影响时钟测量。
FFT运算将数据便换成幅值,注意最高幅值的信号。因为波形的数据是方波和含有其他分量(大部分是奇次谐波),只要注意幅值频谱的最大值就能够找到最高幅值信号的位置,它就是捕捉到的时钟基波。
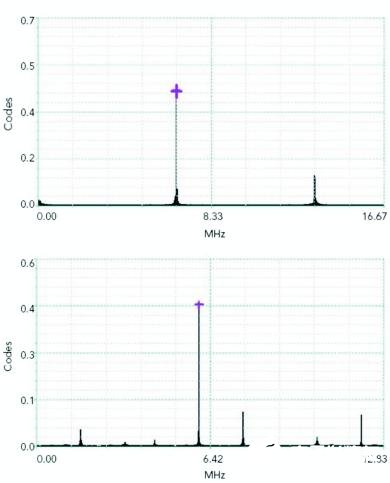
图2Nextest公司混合信号波形工具显示160MHz时钟的频域表示方式
a)用33.333MHz捕捉;b)用25.666MHz捕捉
160MHz时钟由33.333MHz和25.666MHz采样率捕捉的频域谱图如图2所示。FFT频率数据分辨率与两个因素有关,即采样率和样本数。傅立叶频率表达方式是fF=fs/N,图2实例有两个取样率,故有两种分辨率:
33.333MHz/32768=1017。25Hz
25.666MHz/32768=783.28Hz
样本数应在测试时间和分辨率之间做出权衡。用来测量160MHz时钟是,拥有比1KHz更好的分辨率就相当不错了,特别是可在33MHz基本速率的测试器上进行测量。如果需要更好的分辨率,则可能需要付出代价,因为由此开始FFT运算时间加大幅增加。
你也可以用24.5Hz分辨率去捕捉一百万个样本,但是,一百万个样本的FFT即使由双Xeon核电脑做运算也不得不用几秒钟时间。而且,在这方面较慢速度的测试仪器更具优势,因为取样较慢时分辨率会更高。
注意频率相交点 当你测量得到两个混叠频率时,就要搜索信号的频率列表和找出频率相交点。对被检查的混叠频率写下代码并推断它们的相交点。
最好的办法是相对每种取样率写出两列包括全部候选频率的列表。寻找两列的相交点或匹配点(表1)。
表1候选频率列表
33MHz 6.66 26.6 39.9 60 73.3 93.3 106.6 126.6 139.9 160 25.66MHz 6 19.6 31.6 45.3
57.3 70.9 83 96.6 108.6 122.3 134.3 147.9 160
由于所用实例采用两个正交的取样频率,他们之间没有公共因子,在测试频率范围进入GHz以前它们都不会产生交叠。这不会产生太大的问题,因为多数低价位测试仪器的引脚比较器带宽正好没有进入GHz范围。
当找到匹配电视,能够推断6.666MHz是由33.333MHz捕捉到的,6.0MHz是由25.666MHz捕捉到的,他们是真160MHz时钟的混叠频率。假若它不是准确的160MHz,这种情况仍然一样,因为相对于取样频率,混叠频率将产生同样数量的飘移,出现159.5MHz或160.2MHz等频率。换句话说,这不但是160MHz时钟的解决方案,而是你能够用任何一台数字引脚比较器捕捉到任何频率的解决方案。
分辨率和奈奎斯特问题
当你对比表1内两列候选频率的数据匹配情况时,通常允许有小量偏差。这是考虑到两次捕捉之间频率出现飘移和允许捕捉的非相干性质。然而,由于在奈奎斯特和DC频率附近出现的潜在问题,需要避免使用太大的溢出值。
如果测量的时钟非常接近边界,则要想说明混叠真正属于边界的哪一侧就非常困难了。例如,用33.333MHz取样频率捕捉133.0MHz时钟,会看到在奈奎斯特频段内出现333.333KHz的混叠。但是,该混叠也意味着你真正得到133.666MHz的时钟。而假如你允许太大的溢出,则会拾取到错误的数值。
这里还有比其他频率更难测量的频率,特别是K(整数)倍取样率。如果测量的频率与取样频率完全相同,那么大部分样本会落在全高或全低的一侧。FFT将反映出的高值放在DC收集箱内,而软件可以找出DC与一个由另外取样率取样的混叠频率的相交点。
如上文所述,如果不能从捕捉的波形减去0.5,而且捕捉的频率全部为低,那么将在DC收集箱内检测不到幅值。从捕捉的波形减去0.5后,对实高值附加0.5,对实低值减去0.5,情况与由混叠是北侧频率落入DC收集器相同。电压极性对FFT并不重要。
因此,无需使用昂贵的仪器代替现有廉价的数字测试仪器来测量高频,尽管它的速度比小型数字测试仪器快得多。
责任编辑:gt
-
各类通信测试仪器2019-07-19 2931
-
如何使用低价位仪器测试高速时钟?2021-05-14 816
-
虚拟仪器技术在晶闸管电路测试中的应用2008-09-07 1000
-
测试仪器的结构、工作原理及硬件设计2009-10-06 835
-
测试仪器的虚拟技术性能优化2010-03-05 581
-
安捷伦将高性能示波器带入低价位2009-08-13 740
-
安捷伦推出业界最低价位的USB 2.0信号质量测试选件2013-02-04 1460
-
数字集成电路参数测试仪的设计2016-03-29 963
-
多样化数字接口测试挑战的解决方案——基于可编程FPGA的测试仪器2017-10-19 953
-
蓝牙耳机低价位什么牌子好,蓝牙耳机低价推荐2020-08-11 1253
-
LG电子将在2021年推出更多低价位OLED电视2021-03-03 2769
-
数字lcr测试仪2023-03-14 1049
-
离子平衡测试仪器的构成2023-09-04 1932
-
数字绝缘电阻测试仪的使用方法2024-08-25 5115
-
脉冲测试仪器的使用技巧2024-11-26 1693
全部0条评论

快来发表一下你的评论吧 !

