

传输线的特性阻抗和集总参数阻抗联系和区别
电子说
描述
一、简介
特性阻抗可以说是分布式参数电路中最重要的电气参数,但它也是容易使刚接触射频电路的人感到困惑的话题。由于它的名字里有阻抗二字,暗示着它在量纲上等于电压和电流的比值,但是它和集总参数阻抗必然是不同的,那么传输线的特性阻抗和集总参数阻抗究竟有什么联系和区别?我们来一起探讨,一一解答。
二、传输线的即时阻抗
这里我们讨论的传输线是由两个具有一定长度的导体构成的。为了便于突出问题的重点,以下讨论中的传输线均是理想无损耗的。 如图1所示,假设我们在向右无限延伸的传输线左侧接一个理想恒压源,并且在t=0的时候将开关从断开转换到闭合状态,那么传输线开始感受到电源的“压力”。任何事情都不是一蹴而就的,沿着传输线长度的方向并不是所有的位置都立刻建立起了电势差,电势差的建立需要一个电压传播的过程,而传播的速度是光速。
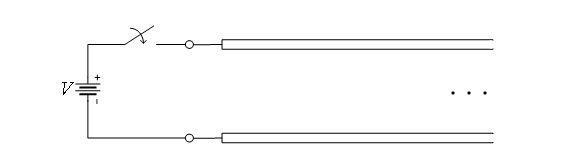
图1 一端外加电源的传输线电路 在开关闭合后的某时刻,沿传输线方向的电势差分布如图2所示。在靠近电源的传输线部分已经建立起电势差,维持电势差需要在传输线的上导体积累正电荷,在下导体积累负电荷。每经过一段时间,电压波会沿着传输线方向推进,而电压波波前的下一段传输线即将在两个导体之间建立电势差。使原本没有电势差的传输线部分建立电势差需要提供额外的正负电荷,搬运正负电荷的工作是由电源来完成的,这个过程是一个给电容充电的过程。
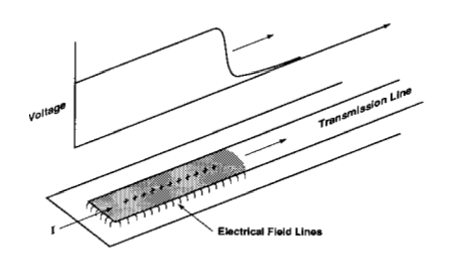
图2 某时刻电压波沿传输线的传播情况 在均匀传输线中,电压波传播的速度是恒定的,即相同时间内一定长度的传输线会被充电,由于横截面均匀,同一长度传输线对应的电容大小也是相同的,因此需要的电荷量是固定的。我们可以认为,在δt这一小段时间内,由δQ的负电荷(电子)被从传输线上导体的某一段转移到下导体对应的位置上,从而建立起该段传输线的电势差。对于电源而言,需要持续输出电流I=δQ/δt,因此在电源看来,这条传输线和一个负载电阻没有区别,这个负载电阻的大小就等于传输线的特性阻抗。如果传输线的横截面是非均匀的,那么随着电压波的传播,不同时刻电源输出电流的大小是变化的,即从电源所在的端口向传输线看去,看到的阻抗是随时间变化而改变的,因此这个阻抗被称为即时阻抗(instantaneous impedance)。即时阻抗等于即将被充电的那一段传输线的特性阻抗。
三、均匀传输线即时阻抗的推导
假设图1中施加的恒压源电压为V,电压波在传播的过程中,传输线上建立起来的电势差等于恒压源电压V。假设单位长度的传输线的等效电容为C,而电压波在传输线中传播的速度为v,那么在一小段时间δt内,电压波传播的距离为,新充电的电容大小为,电源提供的电荷量为 δQ=Cvδt⋅V 那么电压源持续输出的电流大小为 I=δQ/δt=Cv⋅V 而即时阻抗为 Z=V/I=1/(Cv) 公式(1)
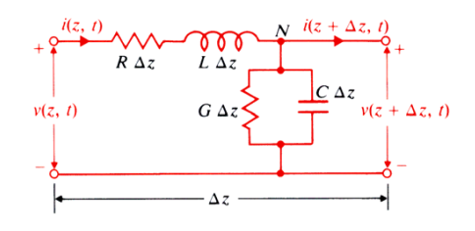
图3 经典的传输线电路模型 另一方面,经典的传输线方程是建立在图3所示的传输线电路模型基础上的,通过电报方程,我们可以推导出传输线的传播常数 以及特性阻抗 在无损耗传输线中R= 0 Ω,G= 0 S。电压波的传播速度可以由γ 推出: 因此有特性阻抗 公式(2) 比较(1)和(2)我们可以看出,即时阻抗和传输线特性阻抗大小是相等的。 如果图1中是一条无限长均匀传输线,它将永远在充电的过程当中,因为电压波永远在前进状态。如果无限长均匀传输线的特性阻抗为Z0,那么它在电路中就可以被等效为一个大小为Z0的集总参数阻抗。
四、传输线电路的时域分析
在上一小节我们了解到传输线的即时阻抗等于特性阻抗,我们可以利用这个规律对图4所示的传输线电路时域响应进行分析。这个电路包含一段长度为l,特性阻抗为R0的无损耗均匀传输线,在传输线坐标z = 0的一端连接着一个内阻为RS的直流电压源V0,在另一端连接负载RL,在t = 0的时候开关闭合,我们将分析在此之后的传输线电压分布情况。
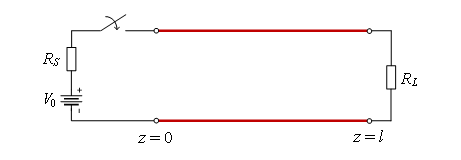
图4 进行时域响应分析的传输线电路 在上一小节的分析中,我们知道电压波在传输线上的传播速度是有限的,即 , 在电压波到达负载电阻之前,电压波并不清楚电路前方是什么情况,它所感知到的是大小为R0的即时负载,因此这段时间内传输线上靠近电源一端的电势差可以通过串联分压求得: 与此同时,电压源持续输出的电流大小为 这个状态一直持续到电压波到达传输线最右端,到达最右端的时间为 此时电压波发现了新大陆,负载电阻RL≠R0。为了使负载电阻RL两端的电压电流满足欧姆定律,会产生沿着-z方向传播的反射电压波当反射电压波在t= 2T时到达最左端,又会产生一个沿着+z方向传播的反射波之后电压波在源和负载之间不断地来回反射,随着时间的推移,最后负载电阻两端的电压趋向于将V1+,ΓL以及ΓS的表达式带入上式进行化简,可以得到VL的简化表达式 最后的表达式是意料之中的,因为图4的电压源为直流源,此时按照经典低频电路的看法,传输线是透明的,图4的电路就是一个负载电阻和电压源内阻的分压电路。 从上述分析可以看到,开关刚闭合的时候,电路是在RS和R0之间进行分压;达到稳态以后,是RS和RL之间进行分压,最后无论传输线特性阻抗R0是多少,都不影响VL的值。
参考文献
[1]
R. J. Cameron, C. M.Kudsia, and R. R. Mansour, MicrowaveFilters for Communication Systems: Fundamentals, Design and Applications, 2nded. Hoboken, NJ, USA: Wiley, 2018.
[2]
A. E. Atia and A. E. Williams, “A solution fornarrow-band coupled cavities,” COMSAT Laboratories Tech. Memo. CL-39-70, 1970.
-
 1926_356
2022-04-21
0 回复 举报非常感谢这篇文章,解开了我的疑惑。 收起回复
1926_356
2022-04-21
0 回复 举报非常感谢这篇文章,解开了我的疑惑。 收起回复
-
关于传输线阻抗的那些概念你都知道吗2024-02-02 2780
-
什么是电缆的特性阻抗?2023-01-09 4474
-
什么是特性阻抗?2019-06-03 2639
-
特性阻抗的计算方法和影响因素2019-05-30 6072
-
特性阻抗怎么计算2018-08-21 79844
-
信号传输线及其特性阻抗2018-02-08 4853
-
对特性阻抗的深度解析2018-01-24 7333
-
传输线的特性阻抗2017-12-29 2614
-
传输线及其特性阻抗2015-01-23 8048
-
无极线PCB设计--特性阻抗的计算及测量2012-06-02 6824
-
高速设计中的特性阻抗问题2012-04-13 4479
-
PCB信号传输线的特性阻抗控制2012-03-31 5546
-
pcb layout培训基础之传输线的特性阻抗2011-11-21 5921
-
传输线特性阻抗2009-09-28 6003
全部0条评论

快来发表一下你的评论吧 !

