基于WLS-KF算法实现对目标较高精度的定位和跟踪研究

引言

卡尔曼滤波（KF）是一个不断预测、修正的递推过程，已经越来越多地应用于动态数据处理中。然而在KF模型中，要求观测方程是线性形式、状态噪声和测量噪声是白噪声。为了解决这种矛盾，将KF理论应用到非线性领域中，扩展卡尔曼滤波（EKF）应用而生，它围绕状态估计值对非线性系统进行一阶Taylor展开使其线性化，但它存在如下不足：一是当非线性函数Taylor展开式的高阶项无法忽略时，会产生较大的线性化误差；二是EKF假定噪声均为正态白噪声，但是一个正态自噪声经过非线性变换后通常不再呈现正态性；三是只有在雅可比矩阵存在时才能线性化，而很多应用中雅可比矩阵很难求。针对这种情况，Julier和Uhlmann等人提出了一种基于非线性变换——Un-scented变换（UT）的卡尔曼滤波算法（UKF）。它通过确定性采样得到的一组sigma点，可以获得更多的观测假设，对系统状态的均值和协方差的估计更为准确，同时由于该算法采用了非线性的状态方程和观测方程，从而避免了线性化误差。目前，EKF和UKF算法被广泛应用于GPS非线性动态滤波研究中，并取得良好的定位效果。

本文给出了一种加权最小二乘一卡尔曼滤波（WLS-KF）算法，它利用一组离散采样点，通过WLS方法产生近似线性化预测模型，然后用KF算法对此模型进行校正。以该算法为思路，将其应用在GPS非线性动态滤波定位解算中，仿真结果表明该算法精度介于EKF和UKF之间，从而实现了对目标较高精度的定位和跟踪。

1 算法描述

1．1 WLS算法

LS算法是现代测量技术中数据处理的基本工具，这种方法的特点是算法简单，在估计解算时，不需要知道与被估计量以及观测量有关的任何统计信息。

设X为待估参数矢量，观测矢量为L。观测方程为：

式中：A是系数矩阵；f（X0）表示用先验参数计算的理论观测向量；b表示拟合后的残差；△X是对先验参数的小修正向量。

LS算法的指标是使各次观测量与由参数估计得到的观测量之差的平方和最小，即：

计算完测量更新方程后，整个过程再次重复，上一次计算得到的后验估计被作为下一次计算的先验估计。

1．3 WLS-KF算法

1．3．1 基本思想

算法基本思想是通过WLS方法计算随机变量经过非线性变换后的分布参数，它利用离散个加权点来确定近似直线。

设待确定的近似线性化模型为：

2 实验结果与分析

基于运动载体为质点的假设建立目标运动模型，考虑一个二维平面曲线运动系统，状态定义为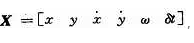，分别表示二维方向上的位置变量、速度变量、载体相对于起始位置的转弯角度及接收机钟差。 

       系统状态方程为：

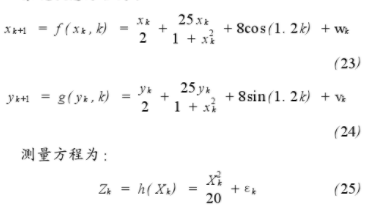
式中：wk，vk和εk为相互独立的高斯白噪声序列，wk～N（0，10），vk～N（0，10），εk～N（0，1）。此系统是具有可加噪声的离散非线性时变系统，观测时间为100 s，观测周期为1 s。WLS-KF和EKF，UKF算法的二维预测结果分别如图1，图2所示，预测结果误差分析见表1。

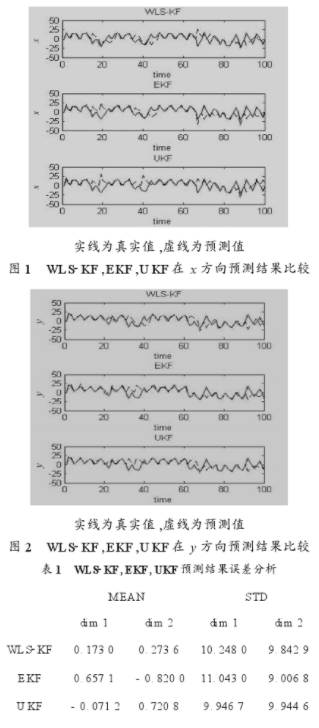
为便于比较，算法中使用的随机数据均来自于提前保存好的随机序列。结果表明，WLS-KF算法的计算量适中，精度介于EKF和UKF之间，且效率同KF接近。

3 结语

本文引入了一种基于加权最小二乘的线性化方法，将其与KF算法相结合，给出了可以应用于GPS非线性动态滤波系统的WLS-KF算法。该算法不需要求偏导数，算法精度介于EKF和UKF之间，可以实现对目标较高精度的定位和跟踪，有一定的应用价值。

责任编辑：gt