动态电路中零输入响应的一阶齐次微分方程解析

动态电路中无外施激励电源，仅由动态元件初始储能所产生的响应，称为动态电路的零输入响应。

RC电路的零输入响应

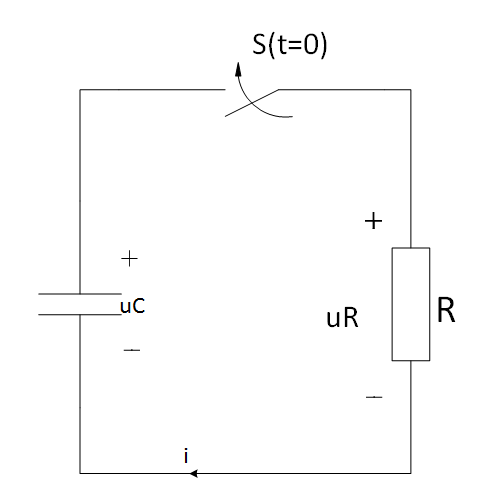
开关S闭合前，电容C已充电，其电压u_C=U_o。现把开关动作时刻取为计时起点(t=0)。开关闭合后，即t≥0+时，根据KVL可得

　　　　u_R-u_C=0

　　将u_R=Ri(对R，电流、电压的参考方向是关联参考方向)，i=-C(du_C/dt)(对电容C，电流、电压的参考方向是非关联参考方向)代入上述方程，有

　　　　RC(du_C/dt)+u_C=0

(齐次线性方程dy/dx+P(x)y=0

通解为y=Ce-∫P(x)dx(C=±e^C1)

对于RC(du_C/dt)+u_C=0，u_C=Ae^-∫(1/RC)dt=Ae^-(1/RC)t

　　　　(RCp+1)Ae^pt=0)

这是一阶齐次微分方程，初始条件u_C(0₊)=u_C(0_-)=U₀，令此方程的通解u_C=Ae^pt，代入上式后有

　　　　(RCp+1)Ae^pt=0

相应的特征方程为

　　　　p=-(1/RC)

根据u_C(0₊)=u_C(0_-)=U₀，以此代入u_C=Ae^pt，则可求得积分常数A=u_C(0₊)=U₀。

　　电路中的电流为

　　　　i=(U₀/R)e^-(1/RC)t

电阻上的电压

　　　　u_R=u_C=U₀e^-(1/R)t

　　由于p=-1/RC，这是电路特征方程的特征根，仅取决于电路的结构和元件的参数。当电阻的单位是Ω，电容的单位为F时，乘积RC的单位为s，它称为RC电路的时间常数，用τ表示。引入τ后，电容电压u_C和电流i可以分别表示为

　　　　uC=U₀e^-t/τ

　　　　i=(U₀/R)e^-t/τ

  RL电路的零输入响应

过程与RC电路类似，从略

　　τ=L/R

　　i=I₀e^-t/τ

　　u_R=RI₀e^-t/τ

　　u_L=-RI₀e^-t/τ