

怎么设计实现一阶数字滤波器
电子说
描述
小伙伴们一定都用过下面这个无源 RC 低通滤波电路:
其拉普拉斯模型如下:
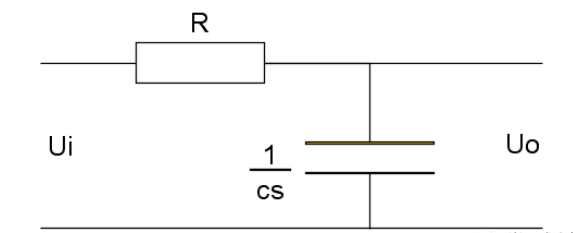
由于
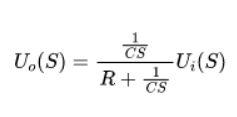
所以:
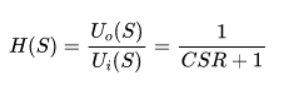
其幅频响应为:
由其传递函数可知,这是一个单极点系统,其阻带满足-20dB/10 倍频程斜率下降。其截止频率为:
如把 C/R 交换位置则变成了高通滤波器,其截止频率依然按上式进行计算。这里也分享一个可在线计算的网址给大家:
http://www.elecfans.com/tools/rclvboqijiezhipinlv.html
其通带增益为 0dB。为什么要先谈谈硬件的一阶滤波器呢? 因为这个是大家最为熟悉的东西,而且也一定学过对其进行幅频响应分析。
既然硬件很容易实现一阶低通或者高通滤波器,那么为什么还要讨论一阶数字滤波器呢?
硬件滤波器需要 RC 器件,R/C 的规格并不能随意选取,受厂家规格限制,其数值并不连续,特殊规格需要定制
数字滤波器非常灵活,一阶数字滤波器计算代价极低。随便一个单片机都可以玩的转。
在满足香农采样定理的前提下可灵活实现截止频率。
数字滤波器
这里直接把差分方程列出来,具体推导就不罗嗦了,有兴趣可以找书看看,比较容易:
其中
表示滤波时间常数,T 表示采样周期。
MATLAB 代码
clc; format compact s = tf('s'); w = 50; % rad/s H = w/(s+w) T = 1/500; Hd = c2d(H,T,'zoh') opts = bodeoptions; opts.FreqUnits = 'rad/s'; opts.XLim = [0.01, 10000]; opts.Grid = 'on'; bode(H,Hd, opts)
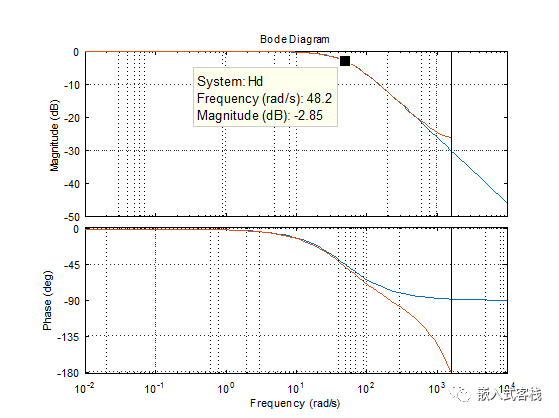
从其响应曲线看为一低通滤波器,相频响应不线性,从其差分方程也看出输出反馈参与运算了,所以其本质是 IIR 滤波器。
上代码
#include
取滤波时间常数为 0.005S,采样周期为 0.2S,为 40 倍关系,来看一下上述代码的滤波效果,波形未失真,效果棒棒哒~
如果将常数修改为 0.1S,看下效果:
由图可见,幅度已经衰减,波形已经失真,传递函数的幅频响应已进入衰减区。所以实际使用的时候,滤波器时间常数尽量取小于采样周期 10 倍为宜,具体可以仿真一下,或者类似上面测试程序测试一下为宜。
总结一下
一阶数字滤波计算简单,实现代价非常低。在滤除高频噪声时应用很广泛。其本质是 IIR 滤波器,为啥要单列出来介绍一下呢?是因为其实现简单,实际使用时也不必进行复杂的仿真。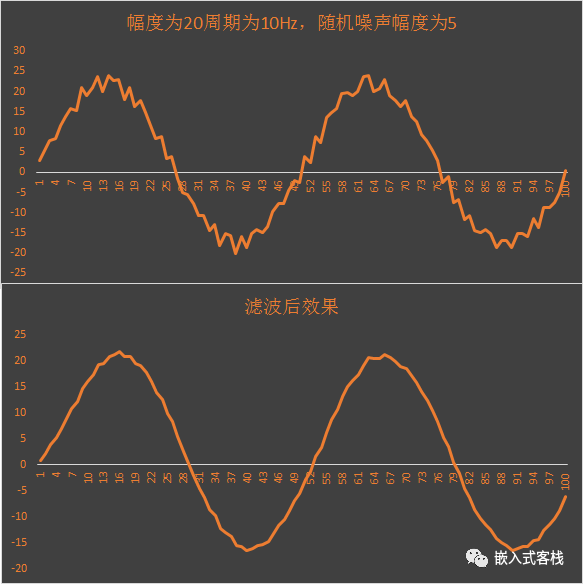

-
数字滤波器是什么 数字滤波器的性能指标2023-02-24 6587
-
FIR数字滤波器设计2022-04-05 6497
-
如何用C语言单片机实现一阶滤波器及高阶滤波器2022-02-28 1279
-
如何使用FPGA实现IIR数字滤波器的设计2020-08-06 1190
-
基于FPGA和MATLAB实现IIR数字滤波器的设计和仿真验证分析2020-07-23 3608
-
LabVIEW如何实现数字滤波器的设计2019-07-26 5644
-
基于matlab的数字滤波器的设计及数字滤波器基本结构2018-06-05 1963
-
使用FPGA构建的数字滤波器设计方案2014-07-24 9467
-
数字滤波器的MATLAB与DSP上设计实现2010-04-12 2133
-
什么是数字滤波器2009-06-30 4247
-
用CPLD实现FIR数字滤波器的设计2009-06-20 1313
-
数字滤波器的设计实验2008-10-30 6147
-
一阶IIR数字滤波器时域滤波效果模拟2008-08-01 1333
-
IIR数字滤波器设计-在FPGA上实现任意阶IIR数字滤波器2008-01-16 2855
全部0条评论

快来发表一下你的评论吧 !

