ABAQUS计算常用的解决不收敛问题的方法

         作者 | 仿真居工  仿真秀专栏作者

在进行有限元仿真计算时，常常会遇到计算不收敛的问题，而且导致求解不收敛的原因也是多种多样的，处理起来也是相当的麻烦。特别是在利用隐式算法的求解非线性问题时，对静态平衡方程进行迭代求解时极易出现计算的不收敛问题，而显式算法基于动力学方程，不需要进行平衡迭代，当时间步长足够小时，一般不存在收敛性问题。无论在哪种算法下出现计算不收敛情况，首先要学会根据软件报错信息排查不收敛的原因，然后对症下药，排除问题。

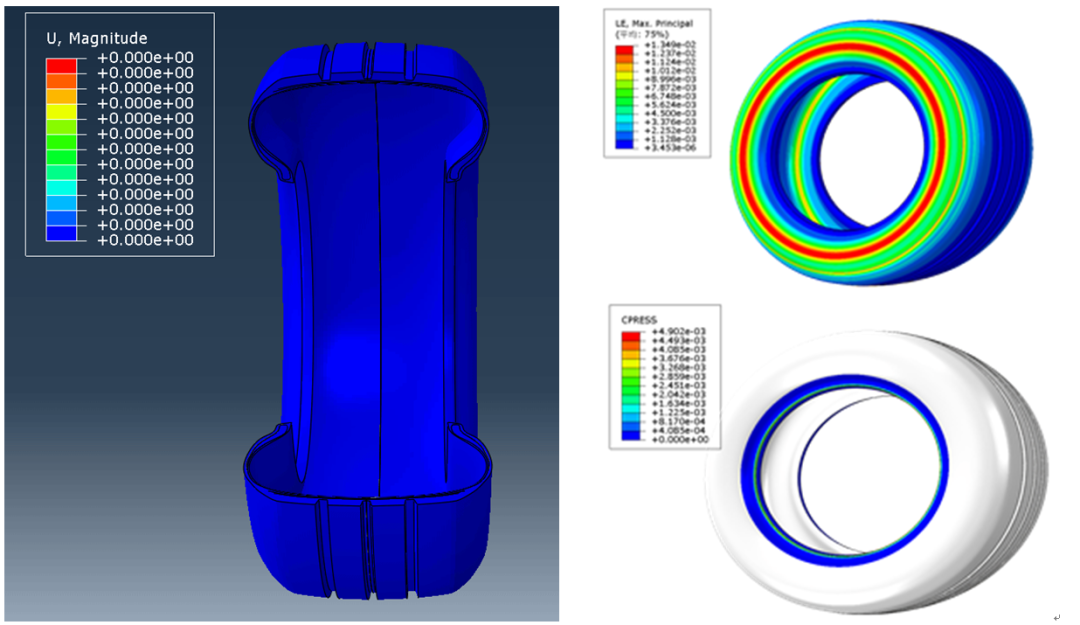
一：不收敛问题的排查方法

●若刚开始进入模型计算阶段就出现不收敛问题，可能原因有：有限元模型网格质量欠佳、边界条件约束不足（出现刚体位移）、接触设置不当、重复导入部件（导致欠约束）、初始载荷过大、初始应力导致的材料塑性、由于单位制未统一间接导致刚度过小或载荷过大等原因，根据提示信息，找出报错位置进行修改。

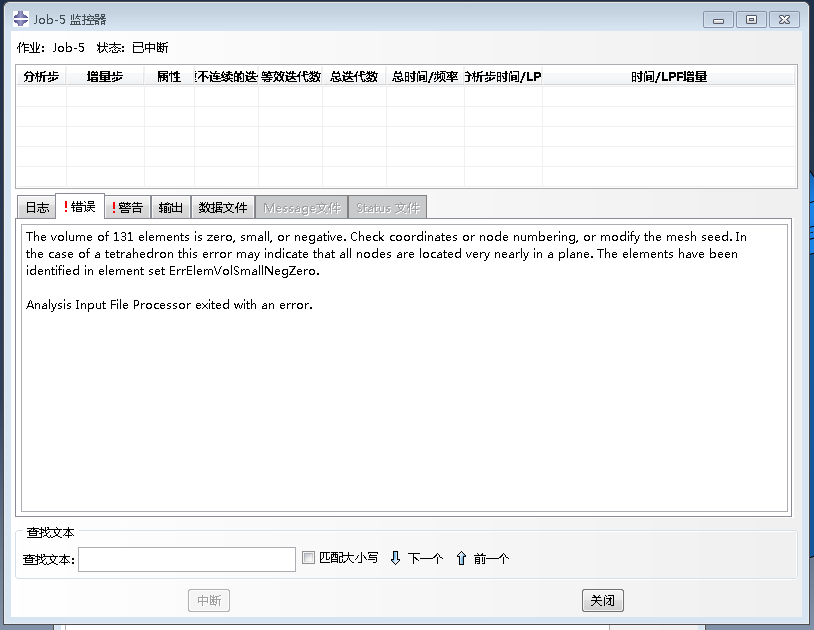
●若在模型计算阶段的中后期才出现不收敛的情况，需要根据已有的计算结果和模型情况进行判断。主要排查方向有：材料软化、失效、屈曲、接触非线性、温度或其他场量的骤变等方面。

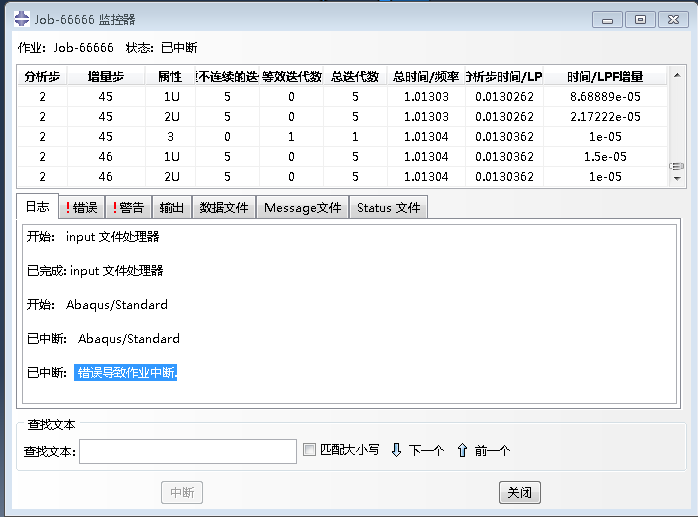
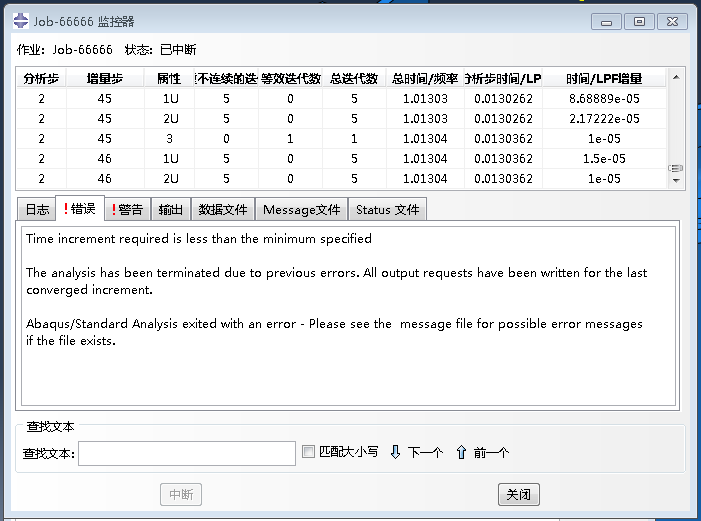
其中最为常见的是随着加载的进行出现畸变单元而导致终止（例如上图），一般来讲此类情况不归属于不收敛问题，而是由于网格畸变导致无法计算单元刚度矩阵，从而无法组装整体刚度矩阵。这种情况的解决办法通常需要重新划分网格，以获得更高质量的网格文件，或者可调整网格类型，亦或采用其他大变形计算方法（ ALE、CEL、SPH 等）进行控制。

●在弹塑性分析过程中出现不收敛的情况时，应首先去掉材料塑性参数，进行最简单的线弹性分析。如果计算收敛，则说明材料的塑性参数有问题，否则说明分析模型中存在其他方面的问题，仔细阅读报错信息。

二：集中常用的解决不收敛问题的方法

1、几何非线性选项解决不收敛问题

在有限元分析中，非线性问题分为三大类：材料非线性、几何非线性和接触非线性。当模型结构发生小变形时，几何方程也就是应变与位移的关系是线性的，此时不用考虑物体形状及位置的变化来列平衡方程，很多情况下小变形分析方法满足精度要求是没有问题的。但是，当结构发生大变形问题时，需要考虑变形对平衡的影响，以此满足精度要求。大变形问题就是几何非线性问题，因为此时几何方程中包括位移的二次项。结构发生几何非线性可以概括为两个方面：

●结构发生大位移小应变。当结构发生大位移小应变时我们就可以认为结构属于几何非线性结构，此时应该在变形后的位形上建立平衡条件，也就是说应该考虑变形对平衡的影响，同时几何方程中应包括位移的二次项。如此一来，平衡方程和几何方程都是非线性方程。

●结构发生大位移大应变，此时属于几何和材料双重非线性。针对橡胶产品的仿真，均属于此类非线性，此时要引入相应的应力应变关系，即赋予橡胶网格超弹性属性。

总的来说，当模型结构经受大变形，那么其几何形状的变化可能会引起结构的非线性响应。位移的大小会影响结构响应，若未考虑几何非线性则难以收敛。分析大变形或大应变问题时，在分析步的设置中打开几何非线性选项，程序会在分析时考虑大变形或大应变对结果的影响。

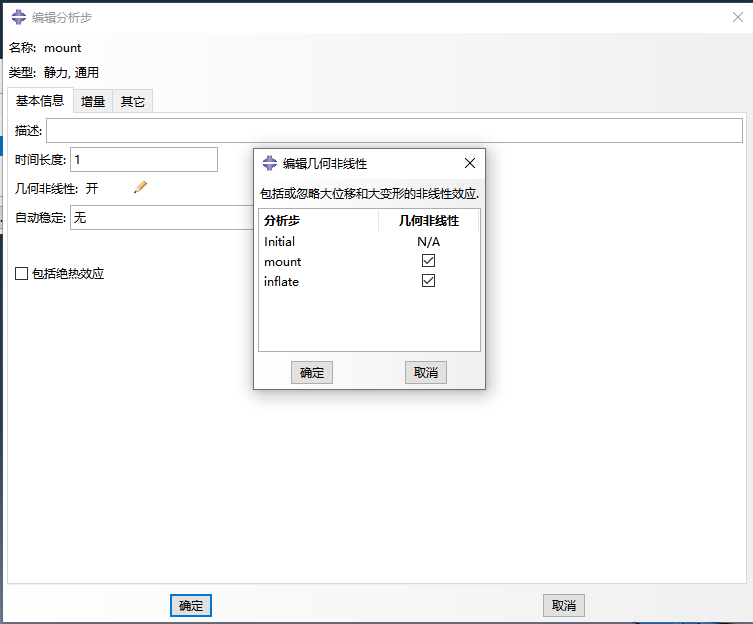
2、合理设置自动稳定解决不收敛问题

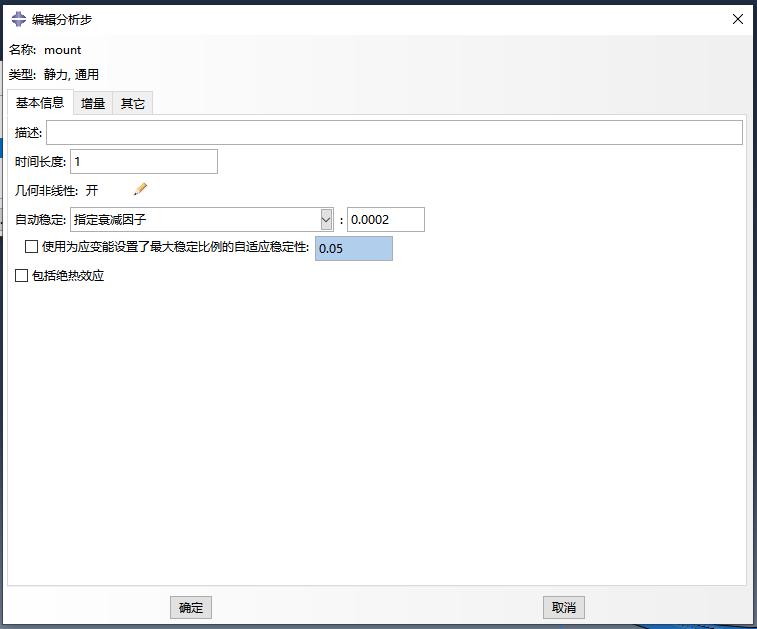
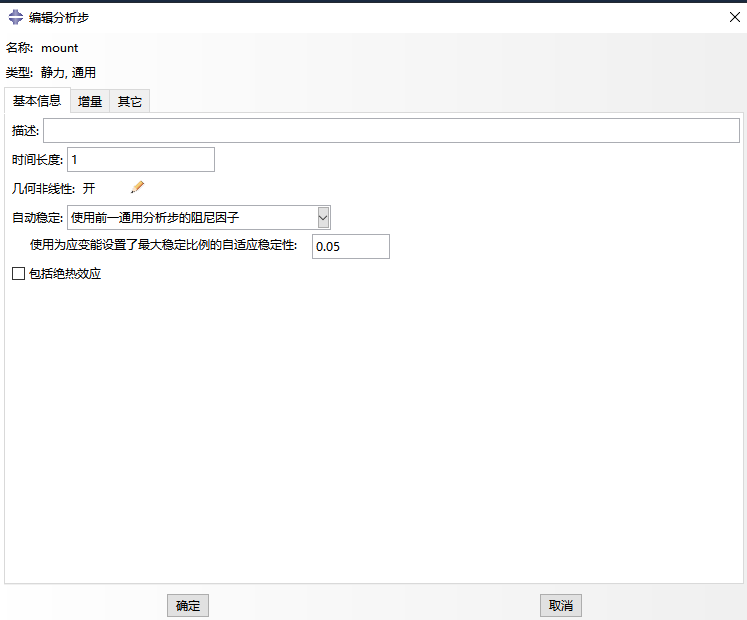
除了几何非线性开关，在分析步中还可以选择自动稳定功能来解决计算不收敛的问题。自动稳定的本质是引入粘性规划系数提高收敛性能，使得刚度矩阵中具有接近零或是负的特征值的时候，也能够计算获得虚拟解。但是粘性系数太小、太大都不行：太小不能解决收敛性问题，太大会使得到的解不正确。虽然ABAQUS软件默认是不考虑自动稳定，但是提供了三种方案并内置了默认参数，分析时可根据具体问题选择恰当的自动稳定条件，解决计算不收敛问题。

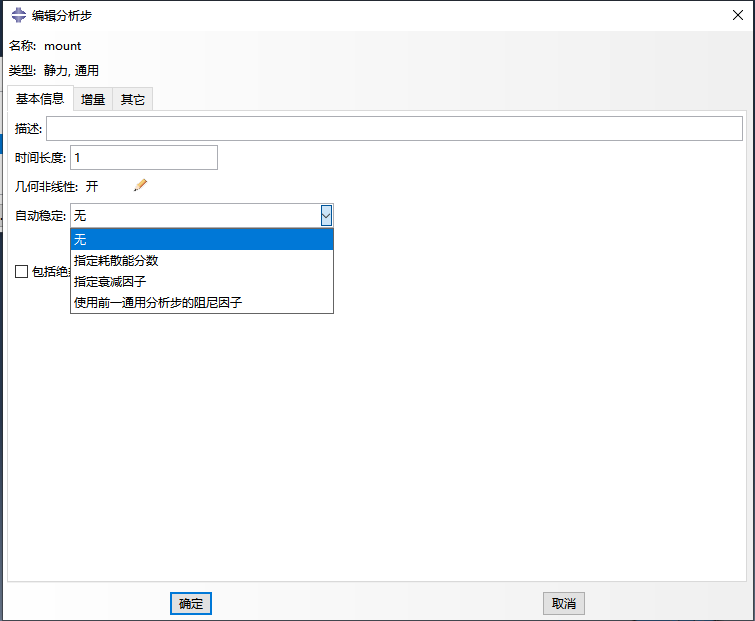
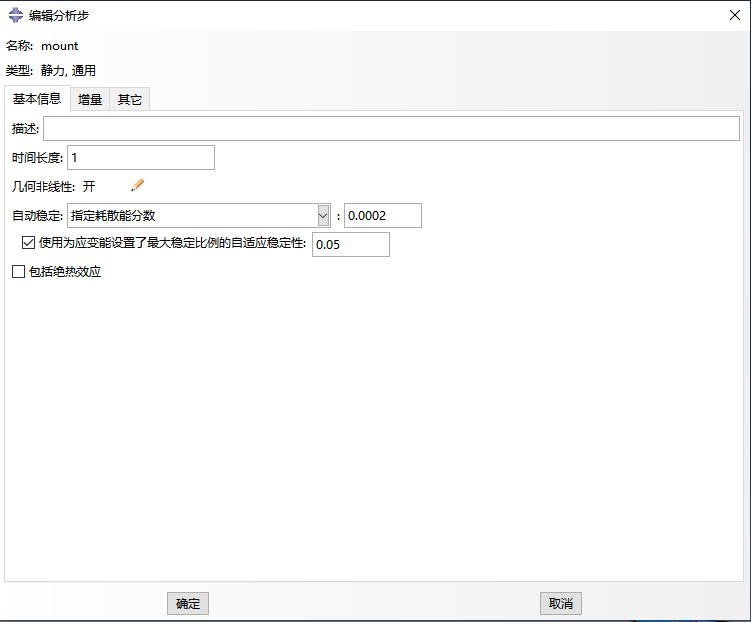
3、划分网格和选择单元类型考虑不收敛问题

有限元方法的计算基础就是网格模型的质量。绝大多数不收敛问题均是由于网格质量欠佳导致的，所以在前期划分网格和选择单元类型时，要注意以下几个问题：

●在变形前和变形后，单元的形状都要保持规则，不要发生严重扭曲；

●大变形区域的网格密度要适当，过粗或过细的网格都可能导致收敛问题；

●在弹塑性分析中尽量不要使用二次六面体单元，以免出现体积自锁现象。建议使用非协调单元、一次减缩积分单元和修正的二次四面体单元进行分析。

4、 优化接触属性解决不收敛问题的思路

在接触分析中出现不收敛的情况，首先要核对接触属性的设置，确保各接触面设置无误。细化接触面网格，减小初始增量步，建立确定的接触关系。模型中不重要的接触修改为绑定约束，可以消除刚体位移的同时大大减少了计算时间。

5、调整通用求解控制属性解决不收敛问题的思路

对于简单的非线性问题，一般不需要调整求解控制参数，采用软件默认设置就能使求解收敛。但对于高度非线性问题难以收敛的情况，可调整求解控制参数来满足收敛条件。例如， Abaqus 默认允许一个增量步内最多进行12次迭代，若不能达到稳定则判定计算不收敛，此时，可通过迭代次数，实现该增量步的计算的收敛。

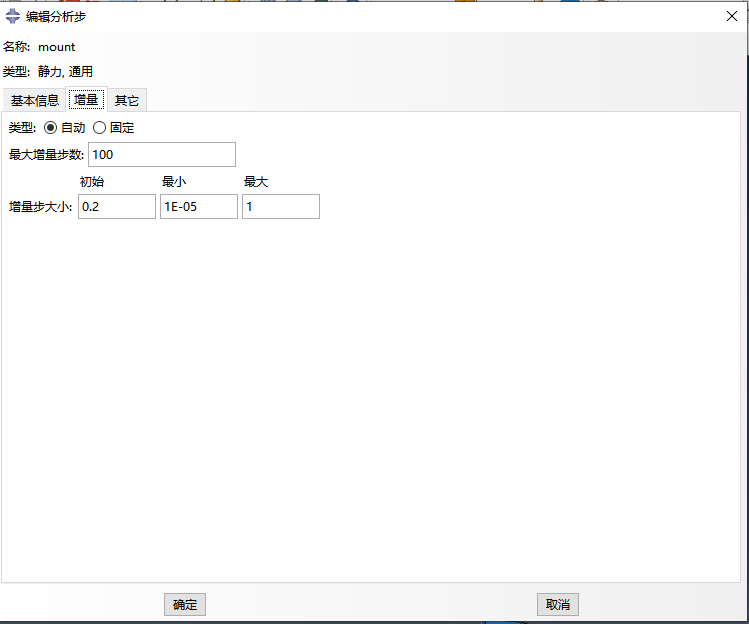
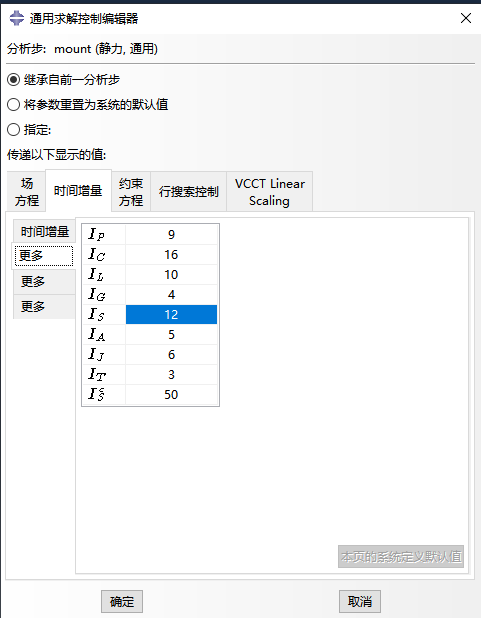
对于可以完成inp文件处理但在初始步出现计算不收敛的情况，检查其在达到迭代次数限制以后的时间增量，如果不是很小时，可以通过调整初始增量步和最小增量步尝试再次求解。但要注意太小的时间增量意义不大，应该从模型当中是否有错误去考虑问题。