如何在VHDL中解决综合工具使用转化问题

引言

VHDL是一种硬件描述语言，于1983年被IEEE制定为国际标准IEEE1076。近年来国内引进和出版了不少教材，使其在国内得到迅速推广。由于VHDL最初目的是为了实现硬件的建模而被提出的，所以其措施能力超越了数字逻辑集成电路的范围。而现有的EDA工具基本上只能支持VHDL的子集，特别是针对FPGA/CPLD器件进行的不同的综合工具，其综合子集并非统一，不少初学者很难掌握。即使是部分有经验的设计者，对于通常高级语言中都会涉及的循环语句，在VHDL中往往也不能运用自如，甚至无法表达此类逻辑，从而限制了VHDL的应用水平。例如，VHDL的并行堆排序描述就是一个比较典型的例子。该实例十分类似通常数据结构的描述，推广前景诱人；但只能通过仿真，却不能在目前任何一个EDA工具进行综合，导致无实用价值。

本文从高级语言涉及最多的Loop语句出发，讨论如何在VHDL中解决这类问题。

1 无法综合的Loop动态条件

VHDL中Loop表达式有三种体现形式：While……Loop、For……Loop和单独的Loop语句。它还支持Next、Exit和标号，因此，循环语句的表达能力大于常规的C或PASCAL语言。程序1是利用For语句和While语句描述插入算法的部分代码。

程序1 不可综合的VHDL循环语句

……

for I in 2 to Length loop ---Length为一个变量

Temp：=MyList（I）；

J：=I；

While（j》1）and MyList（j-1） MyList（j）：=MyList（j-1）;

j：=j-1;

End loop;

MyList（j）：=Temp；

End loop;

……

对于第一个For语句，EDA工具Synplify综合时将会给出无边界的范围错误提示。

@E：“H：.vhd”|for loops with unbound ranges should contain w wait statement

即使部分优秀的综合工具，例如ORCAD Express、Mentor Grpahs QuickHDL等能够综合第一个For语句，也无法支持第二个While条例表达式。ORCAD Express将给出表达式不可静态计算的错误提示。

。.vhd（45）：Error，expression does not evaluate to a constant.

由于程序1在C程序员看来是没有问题的，因此，初学者往往不能解决好此类问题，从而使学习陷入困境，无法充分利用VHDL来表述逻辑。

2 直接代换法

对于第一类无边界的范围错误问题，可以用循环的综合机制转化为相应的语句。例如下面代码：

for I in 0 to 1 loop

Out_Bus（i）《=In_Bus（i）；

End loop；

其对应综合后的电路见图1。

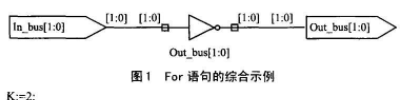
图1 For语句的综合示例

相应的，也可以用下列语句直接代入代换：

Out_Bus（0）《=In_Bus（0）;

Out_Bus（1）《=In_Bus（1）；

程序1可以采用下列VHDL代码表示：

K：=2；

Temp：=MyList（2）;

If（MyList（1） MyList（2）：=MyList（1）;

J：=1;

End if;

MyList（J）：=Temp;

J：=3;

Temp：=MyList（3）;

If（MyList（2） MyList（3）：=MyList（2）;

J：=2;

End if;

If（MyList（1） MyList（2）：=MyList（1）;

J：=1;

End if;

MyList（J）：=Temp;

……

然而，这种使用方法要求设计者清楚循环条件一定会执行的次数，否则将无法实施。当循环次数比较大时，代码编写工作量将十分庞大，因此可以采用第二种方法——边界扩充法。

3 边界扩充法

边界扩充法是指在边界未定时，可以将边界定为最大可能的范围，即用静态表达来替代。例如程序1的代码可以改写为：

constant MAX:integer=100; --MAX必须大于MyLen所有可能的取值

……

Out_loop:for I in 2 to MAX loop

Exit out_loop when I》MyLen; --MyLen为变量

Temp：=MyList（I）;

countj：=I;

inter_loop:for j in I downto 2 loop

countj：=j;

exit inter_loop when MyList（j-1） MyList（j）：=MyList（j-1）;

End loop;

MyList（countj）：=Temp;

End loop;

尽管这种方法可以处理未知边界和未定表达式的情况，但十分消耗空间，特别是当MyLen相对MAX比较小的时候，代价非常大。此时，可以利用时间换空间的方法进行转换。

4 计数器法

计数器法是指引入时钟和计数器，用计数器对边界条件进行控制，也可以将动态表达式直接代入转化相应的静态表达式。例如，上述代码的For条件可以用下列代码替换：

if（Reset=‘1‘）then

I：=2;

Elsif clk=‘1‘and clk‘event then

Temp：=MyList（I）;

J：=2;

While（j》1）and MyList（j-1） MyList（j）：=MyList（j-1）;

j：=j-1;

End loop;

MyList（j）：=Temp;

I：=（I+1）;

If（I=MyLen+1）then I：=2;end if;

End if;

相比原来的代码，引入了1个时钟和1个复位。但综合开销最大的循环语句却被取代了，因此，综合产生门的数目将大幅度下降，但处理时间将相应延长到原来循环条件范围。

本刊网络补充版中发表了四个源代码，分别为不可综合例子、直接代换法、边界扩充法和计算器法，内部都有相应注释。其中计数器法改进为双计数器方法。

结语

以上三种方法各有优缺点，不可一概而论，可以根据实际情况处理。直接代换法一般用于循环次数少的情况；边界扩充法一般用于循环次数接近最大边界时；计数器方法一般用于芯片内部时钟相对信号时钟快许多的情况。

责任编辑：gt