结环行器的设计流程

【摘　要】根据结环行器理论，推导出通用的设计公式，提出设计流程，并据此设计出二公分波段带线环行器，验证了方法的有效性。
　　关键词：结环行器　设计流程　铁氧体器件
　　
1　引　言
　　带线结环行器是一种用途广泛的铁氧体器件，虽然其理论研究和设计实践具有深厚的基础，但对一般设计者来说却显得深沉而无从着手。本文把结环行器的场理论与路理论结合起来，推导出一些通用的设计公式，提出一个简明的设计流程，并以此研制出二公分波段结环行器，为将来更有效的计算机辅助设计打下基础。
2　设计依据
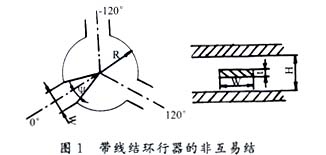
　　图1是环行器的结构示意图，其核心是一个外加恒定磁场的铁氧体非互易结，中心导体可以是圆盘形、Y形、双Y形或三角形等各种形状。网络理论分析可证明一个匹配的无耗对称三端结就是一个环行器，用散射矩阵表示为：
　　　　　　　　

对应散射矩阵的三个本征值为：
　　　　　　　　　　　　　　　　
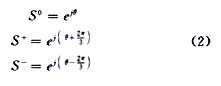
根据导纳矩阵与散射矩阵的关系，可导出相应导纳本征值
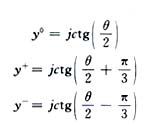　　　　　　　　　　　　　　　　     (3)

式中θ是任意值，消去后可得
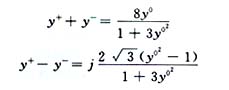　　　　　　　　　　　　　   (4)

　　这就是三端结环行器的两个环行条件，它是一个通用公式，也就是说不论何种结构形式的三端结环行器，只要能导出它的三个导纳本征值，并令其满足上式，则它必然是一个理想环行器。
　　为了导出不同结构形式的导纳本征值，可以从结的场理论或路理论出发。对于圆盘结环行器　，只考虑三个低次模，得〔1〕
　　　　　　　　　　　　　　
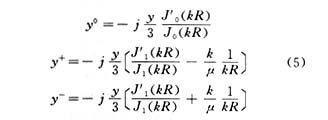
式中，y为以未知结导纳Yj归一化的导纳参量
　　　　　　　　　　　　　　　　　　

而Yf为铁氧体带状线的特性导纳
　　　　　　　　　　　　　
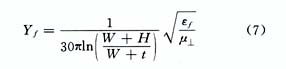
当然还可导出其它结构形式，例如Y形、双Y形甚至包括集中元件环行器的导纳本征值，这里不一一列出。
　　令式（5）满足环行条件式（4），可以得出一组参数（kR，y，k／μ）。反过来说，如果按这组参数来设计器件，则必然是一个理想环行器，因此环行器的设计在于仔细研究这组参数，看看它们彼此有什么关系，相互间有什么制约，以便合理选取。
　　y参数：归一化的导纳参数，从式（6）、（7）可看出，它主要取决于环行器的结构参数W，H，Ψ，铁氧体介电常数εf以及有效张量磁导率μ⊥。结构参数及εf通常事先选取，所以，y主要取决于铁氧体磁参数μ⊥。
　　k／μ参数：张量磁导率非对角分量除以对角分量，它也是铁氧体的磁参数。
　　kR：贝塞尔函数的宗量，其中R是铁氧体样品的半径，而μ⊥，μ，k这些磁参数取决于铁氧体归一化磁矩和内磁场：
　　　　　　　　　　　　
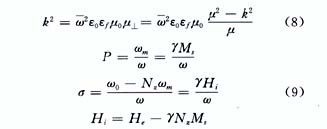
式中，Ms为铁氧体饱和磁化强度，Hi，He为铁氧体内部、外部磁化场，Nz是磁化场方向的退磁因子，曲线见图2和图3〔2〕。因此当工作频率和铁氧体材料选定后，μ⊥，k／μ的大小由外加磁场决定，可见铁氧体半径与外加磁场是两个重要设计参数，是实现两个环行条件的具体操作。
　　　　　　　　　　　　
　　　　　　　　　　　　　
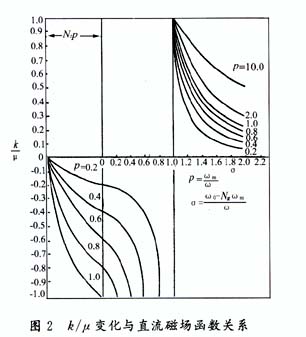
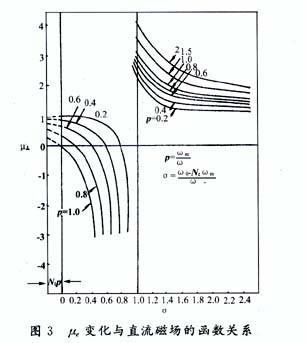
　　现在来分析一下设计过程：
　　确定kR：即选取半径R以及选好磁场工作点，确定μ⊥，k／μ，得到kR。
　　计算y：已知kR，由式（4）第一式计算y，通常y是无法与连接环行器的传输线（一般特性阻抗为50Ω匹配的，故必须加匹配网络，或者改变结构参数，尤其是H或Ψ，使系统匹配。
　　计算k／μ：已知kR及y，由式（4）第二式计算k／μ，若计算结果符合σ所确定的k／μ值　，设计成功，否则需重新确定kR，进行循环计算，直到符合条件。
3　设计流程
　　经过上面的分析可写出环行器的设计流程如图4所示。为了简明起见，对环行器的匹配网络以及优化过程没有展开来叙述。设计只适合于窄带器件。
　　　　　　　　　　　　　
　　　　　　　　　　　　　
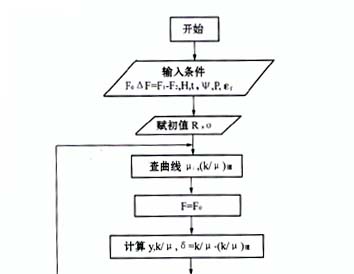
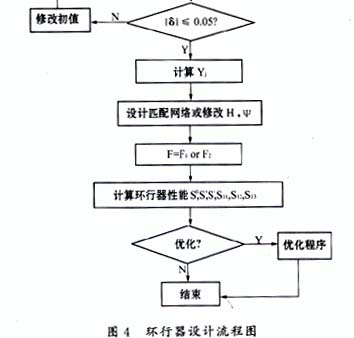
　　从设计流程图可以看出，环行器设计的关键是选取R，σ，为此要给出一个合理范围，对于低场器件，为了避免零场损耗，P通常选在0．4～0．7之间，而外加磁场要使材料饱和，即σ＝0，由此可得出　
　　　　　　　　（k／μ）理＝P
　　　　　　　　μ⊥＝1－P2　　　　　　　　　　　　　　　（10）

　　至于R的选取，若考虑器件小型化，则应尽可能小，反之，若是高功率应用，则必须大一些　，通常kR在0．8～1．8之间确定，对于高场器件，必须使σ＞1，P＞1，当然也不能太大，大致范围为1．5＜σ＜2，1＜P＜2。
4　实验结果
　　按上述流程来设计一个二公分波段带线圆盘结环行器。
　　输入条件：F0＝16GHz，ΔF＝F1～F2，H＝2．2mm，t＝0．2mm，W＝0．8mm，Ψ＝10°，所用材料的饱和磁化强度为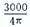KA/m,即P＝0．52，而εf＝15。赋初值：R＝1．5mm，σ＝0，得（ k／μ）理＝0．52，μ⊥＝0．72，kR＝1．65。
　　当把上述条件代入式（4）进行计算后，发现δ不能满足条件，须修改初值，为此，样品半径改为R＝1．36mm，磁场工作点不变，这时kR＝1．5。
　　计算结果y＝6．81，k／μ＝0．47，｜δ｜≤0．05。这个结果说明二公分波段这类频率较高的器件，样品尺寸的选取是很灵敏的，可以进一步计算Yj也就是结阻抗Rj＝1／Yj＝8．55Ω，这是一个低阻抗结，可以采用递增式网络与50Ω传输线匹配，图5是这个器件的性能曲线。
                      
                      
                         

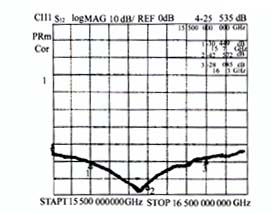
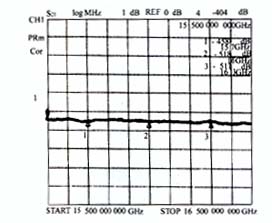
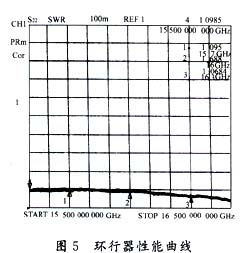
5 结束语
　　本文提出了环行器设计流程，并以二公分波段结环行器的研制为例，证实了这个过程的有效性。这个流程不仅可用来设计窄带环行器，同时也为涉及匹配、宽带、优化等更有效的环行器计算机辅助设计打下了基础。

　　参考文献

　

1　魏克珠，李士根，蒋仁培．微波铁氧体新器件．北京：国防工业出版社，1995
2　C．E．Fay，R．L．Comstock．Operation of the FerriteJunction Circulator．IEEETrans．MTT，1965；13（1）：15－27