机器学习算法的特征工程与意义详解

1、特征工程与意义

特征就是从数据中抽取出来的对结果预测有用的信息。

特征工程是使用专业知识背景知识和技巧处理数据，是得特征能在机器学习算法上发挥更好的作用的过程。

2、基本数据处理

数据采集

• 需要思考那些数据有用
• 数据是否容易采集到
• 线上实时计算的时候获取是否快捷

数据清洗

数据清洗做的事情：洗掉脏数据

思考角度：

1、单维度考量

身高3m的人？显然不可能

一个月买脸盆墩布花了10w的人？也不太可能

组合或统计属性判定

号称在美国但IP却一直在大陆的新闻阅读用户？

要统计一个人是否会去买篮球鞋，然而你的样本中女性占80%？

2、统计方法

使用箱线图/boxplot上下界

取出缺省值多的字段

不可信的样本要去掉，缺省值极多的字段考虑不用

数据采样

分类问题中，很多情况下正负样本是不均衡的。比如患某些疾病的患者和健康人。

大多数模型对正负样本比是敏感的（如逻辑回归LR）

解决方法：随机采样、分层采样
如果是正样本>>负样本，而且量都很大：在正样本下采样。（如正样本200万个，负样本20万个，此时在正样本中随机采样20万个，正负样本1:1构建分类器）
如果是正样本>>负样本，量不大：1、采集更多数据；2、可以oversampling，即过采样（如有10万正样本，1000负样本，最简单的方法是将1000负样本多重复几遍。然而这样做可能会加大过拟合风险，故会将负样本经过一些小的处理。如图像识别里面判断是否为猫，可将图片旋转？镜像处理？加上一些噪声？均可）；3、修改损失函数。

3、常见特征工程

数值型

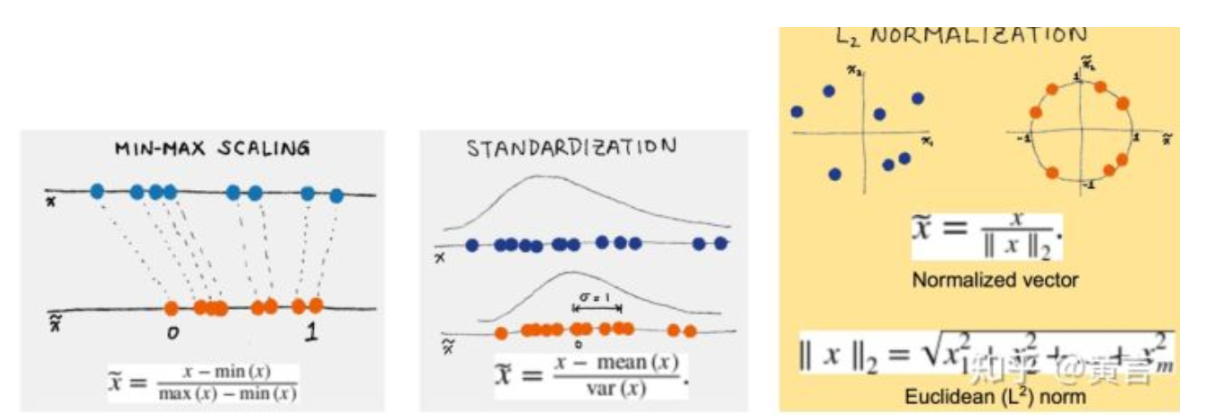
1、幅度调整/归一化
- 幅度缩放Scaling
- 标准化Standardization
- 归一化Normalization

2、将数值进行Log等变化

3、统计值max、min、mean、std

4、离散化

对连续值可以将其离散化，按照一个区间来分（分箱、分桶）

下面代码生成满足标准高斯分布的20个随机数，使用pandas的cut函数可以将数据划分。

import numpy as np
import pandas as pd
arr = np.random.randn(20)
factor = pd.cut(arr,4)

factor
Out[5]: 
[(-0.643, 0.329], (0.329, 1.302], (-1.616, -0.643], (-1.616, -0.643], (-0.643, 0.329], ..., (-0.643, 0.329], (-0.643, 0.329], (-0.643, 0.329], (0.329, 1.302], (-1.616, -0.643]]
Length: 20
Categories (4, interval[float64]): [(-2.593, -1.616] < (-1.616, -0.643] < (-0.643, 0.329] < (0.329, 1.302]]

5、高次与四则运算特征

通过高次多项式或四则运算来将数据升维。

6、数值转为类别

类别型

1、one_hot编码/哑变量

原数据

做one_hot编码之后

注：不适合类别特别多的字段

2、Hash技巧

如上图，将文本型映射成向量

时间型

时间型数据既可以看成连续值，又可以看成离散值。

其他类型

1、文本型

词袋模型/bag of words

word2vec

文本数据预处理后，去掉停用词，剩下的词组成的list，在词库中的映射稀疏向量。

上述向量没有加上词的顺序，可以将词袋中的词扩充到n-gram。下图即为将“Bi-grams are cool！”这句话映射成1个单词和两个单词。

Tf-idf特征

Tf-idf是一种统计方法，用以评估一个字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随它在语料库中出现的频率成反比下降。

TF：Term Frequency

TF(t) = (词t在当前文中出现的次数)/(t在全部语料库中出现的次数)

IDF:

IDF(t)=ln(总文档数/含t的文档数)

TF-IDF权重 = TF(t)*IDF(t)

2、统计特征

加减平均

分位线

次序型

比例型

特征处理示例

4、特征选择方法

特征选择意义：

冗余：部分特征相关度太高了，消耗计算性能

噪声：部分特征是对预测结果有负影响

特征选择VS降维：

前者剔除原本特征里和结果预测关系不大的，后者做降维操作，但是保存大部分信息

SVD或PCA确实也能解决一定的高维问题

过滤式特征选择

评估单个特征和结果值之间的相关程度，排序留下Top相关的特征部分

Pearson系数，互信息，距离相关度

缺点：没有考虑到特征之间的关联作用，可能把有用的关联特征误剔除

相关的Python包：

#SelectKBest选择排名前k个的特征
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
#chi2是卡方统计量
from sklearn.feature_selection import chi2

iris = load_iris()
X,y = iris.data,iris.target
# 之前的X数据集是有4个特征的
X.shape
Out[13]: (150, 4)
# 使用SelectKBest，使用卡方统计量，选出top2的两个特征    
X_new = SelectKBest(chi2,k=2).fit_transform(X,y)
X_new.shape
Out[15]: (150, 2)

包裹式（wrapper）特征选择

把特征选择看做一个特征子集搜索问题，筛选出各种特征子集，用模型评估结果。

典型的包裹式算法为“递归特征删除算法”（recusive feature elimination algorithm）
如用逻辑回归，如何去做？

用全量跑一个模型

根据线性模型系数（体现相关性），删掉5%-10%的特征，观察准确率/AUC的变化

逐步进行，直至准确率/AUC出现大的下滑停止
相关python包

几个参数estimato为选择的模型，n_features_to_select为迭代到最后几个特征值。

from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston

boston = load_boston()
lr= LinearRegression()
rfe = RFE(lr,n_features_to_select=1)
X = boston["data"]
# 数据有13个特征
X.shape
Out[27]: (506, 13)

Y = boston["target"]
names = boston["feature_names"]
rfe.fit(X,Y)
Out[28]: 
RFE(estimator=LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False),
  n_features_to_select=1, step=1, verbose=)

# 使用递归特征删除算法，将数据的13个特征排序，数字为对应特征的序号
rfe.ranking_
Out[29]: array([ 8, 10,  9,  3,  1,  2, 13,  5,  7, 11,  4, 12,  6])

嵌入式特征选择

根据模型来分析特征的重要性（有别于上面的方式，是从生产的模型权重等）

最常见的方式为正则化方法来做特征选择

一般用L1正则化来进行特征选择，用L2正则化来防止过拟合。

from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
iris = load_iris()
X,y = iris.data,iris.target
# 之前的特征数为4
X.shape
Out[6]: (150, 4)
# 使用线性SVM分类器，正则化选L1正则化
lsvc = LinearSVC(C=0.01,penalty='l1',dual=False).fit(X,y)
model = SelectFromModel(lsvc,prefit=True)
X_new = model.transform(X)
# L1正则化后选择的特征数为3
X_new.shape
Out[10]: (150, 3)