同步传感器信号的方法

您是否曾经使用过两个传感器信号来测量同一系统的不同部分？如果没有使用同一数据采集系统测量这些信号，那么在后处理中同步这些信号可能会非常痛苦。它们的采样率和时钟时间可能略有不同，需要偏移。

我们的传感器客户通常需要在多个设备上同步这些独立的数据采集和传感工具。对于一个客户而言，同步是如此重要，以至于我们与他们合作开发了一种解决方案，用于同步我想在此博客中与您共享的两个信号。

需要同步的未对齐数据的示例

执行同步所需的硬件（破坏者：您需要测量一些通用的东西！）

在信号之间重新采样数据以具有共同的采样率

使用“重大”事件确定偏移量

同步数据的最终结果

分析技术可改善同步

结论

数据未对齐的示例

通常在工程中，我们有来自两个独立传感器的相同或相似内容的数据记录，并且想要对齐记录以便在两者之间执行更复杂的分析。但是，即使对于配置为具有相同采样率的两个设备，在每个设备上也会出现与真实采样率的微小差异，并且可能导致这两个设备的采样之间逐渐出现偏差。由于时钟漂移，设备在记录开始时还可能具有不同的内部时间戳记，从而导致记录之间的初始时间偏移。因此，我们要对这些记录执行某种同步，以同时考虑采样率漂移和初始时钟偏移。同步需要既准确又具有合理的运行时间。

图1：蓝色和橙色信号分别记录在两个设备上。他们的录音相似，但是其中之一随时间变化，其中之一被误解为采样率

设备硬件要求

为了确保传感器以我们认为的采样率运行，需要专门的硬件。对于每个正在记录数据的设备，该设备还将产生一个正弦波，从中我们以比实际传感器更高的速率记录样本。我们称其为“同步数据”，并将产生该信号的信号称为“同步信号”。

重新采样以获取通用采样率

为了能够比较两个信号，它们必须具有相同的采样率，因此我们的首要任务是将两个信号重新采样为相同的采样率。为此，我们首先计算信号一与信号二的时间之比，这可以通过比较同步信号的频率来确定（使用傅立叶分析，请参见下图）。然后用一个有理数来近似该比率，其中分子是信号再采样所需的样本数，分母是信号二所需的样本数（更多信息请参见下面的分析技术部分）。通过遵循这种重采样策略，信号的重采样数据中的时间步将保持一致，采样率也将保持一致。

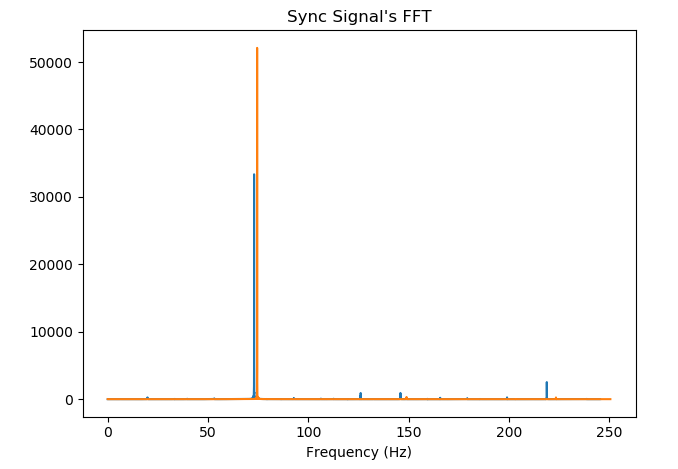
图2：记录未对齐信号时保存的同步数据的FFT

确定偏移

现在我们有两个具有相同采样率的信号，我们必须确定两次记录开始之间的时间偏移。这个问题可以被定义为寻找最佳信号一个偏移吨 ∈（ - LEN（信号 1），LEN（信号 2））？ ？由一些度量，其最好的同步重采样信号。我们还允许用户指定两个信号之间的最大起始时间偏移，以防止由一个信号中的最后几个采样与另一个信号中的前几个采样很好地同步引起误报的可能性。

当使具有大量样本的信号同步时，用于最佳偏移的搜索空间很大，并且计算两个信号如何同步的计算成本很高。直观上，我们避免这种情况的方法是使记录中的“主要”事件同步，因为这些“主要”事件应记录在两个信号中，因此它们的偏移应使信号对齐。考虑到这一点，我们生成了可能包含最佳解决方案的搜索空间子集。为了确定该子集，我们在每个信号中获取“关注点”，并使用在选择一对点（每个信号中的一个）来对齐信号时出现的偏移。在这里，我们将“关注点”定义为信号中发现的任何峰或谷。

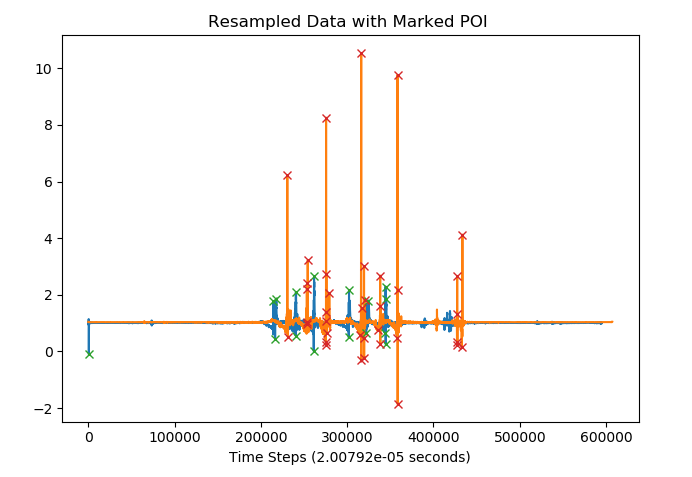
图3：记录已重新采样，并且其“兴趣点”在图上标有“ X”。这些点旨在捕获在两个信号中都已记录的主要“事件”

最终结果：同步数据！

然后根据最佳的兴趣点对（两个信号中的每个信号之一）对信号进行对齐。在我们的案例中，我们选择“最佳”表示产生最大归一化互相关的信号。

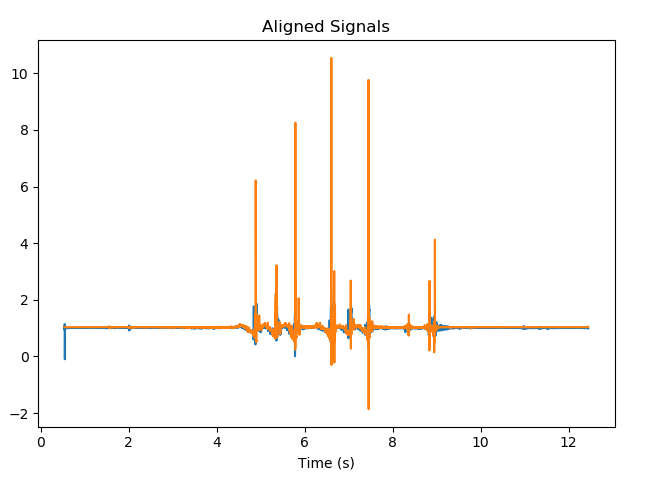
图4：本文开头显示的相同信号，但现在已同步！处理了有问题的时移和频率误差，并调整了信号的时间戳以更好地表示何时记录数据

改善同步性的分析方法

时间跨度比的有理逼近

近似于两个信号之间的时间跨度比的有理数在这种方法中起着至关重要的作用，并且很有可能会得到改进。具体来说，它会产生时间跨度比的最佳有理近似值，其中分母小于1e6，并且大于两个原始信号之一中最大采样数的5倍（以确保对其进行充分的过采样）。

由于时间跨度比率（和原始信号中的点数相同）的差异非常小，因此该方法在用于重采样的点数上可能会有很大变化。更精确地选择有理逼近（通过某种方法，例如计算截断的连续分数）可能会提高其同步信号的能力。

同步指标

标准化互相关在同步评分方面做得很好，但不一定是可以做到的最好。用更准确的同步度量甚至集成度量来代替其使用可能会提高其识别最佳同步配置的能力。

兴趣点（POI）查找

改进POI查找方法将提高找到最佳对齐方式的可能性。更精确的POI查找方法不太明显的副作用是，通过查找较少的误报，将测试较少的非最佳POI对以进行对齐，因此，运行速度将提高。

结论

希望这种快速概述可以帮助您定义如何同步来自两个不同传感器和数据采集系统的数据。总而言之，主要步骤是：

确保两个传感器正在测量相同/相似的物体

以相同速率重新采样数据

查找感兴趣的事件以确定偏移量