为什么使用傅里叶变换 FFT变换的基本原理

1.FFT变换的基本原理

傅立叶变换是数字信号处理领域一种很重要的算法，可以将一个信号从时域变换到频域。傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。

根据原信号的不同类型，傅里叶变换可以分为四种类别：

(1)非周期性连续信号傅里叶变换

(2)周期性连续信号傅里叶级数

(3)非周期性离散信号离散时域傅里叶变换

(4)周期性离散信号离散傅里叶变换

快速傅里叶变换(FFT)，是利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称，但是它是基于复数的，复数DFT写成如下极坐标形式：

 

 

在复数傅里叶变换中，x[n]和X[k]都是复数数组，它包括正频率和负频率。K从0到N-1，0~N/2的频率为正值，N/2~N-1为负值。因为离散信号的频谱是周期性的，其周期等于抽样频率。所以N/2到N-1的频率和-N/2~0的频率是相同的。0点和N/2点的频率值为正负频率的分界。

我们设变换长度N = 2L，将x(n)按照n的奇偶分为两组
x₁(r) = x(2r)
x₂(r)= x(2r+1)

其中r=0,1,…,N/2-1，带入上述复数DFT变换的公式，得到X[k]：

 

 

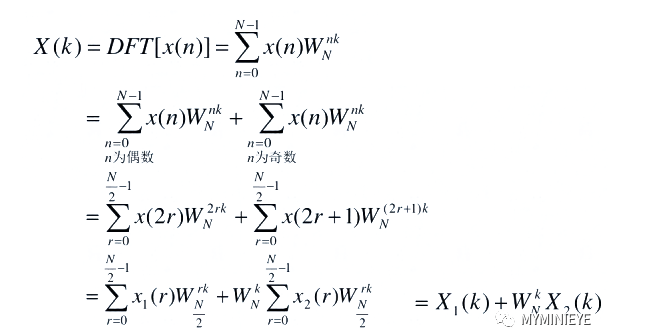
在式子中X1(K)和X2(K)分别是x1(n)和x2(n)的N/2点DFT，因此它只能算出前一半的值，后一半利用

 

 

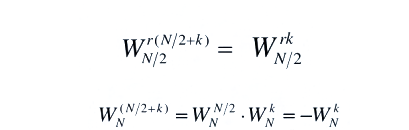
可以得到后半部分X(k)

 

 

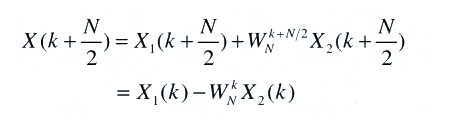
把x(n)的N点DFT合到一起，就是如下的蝶形运算，也是FFT的基本运算单元。

 

 

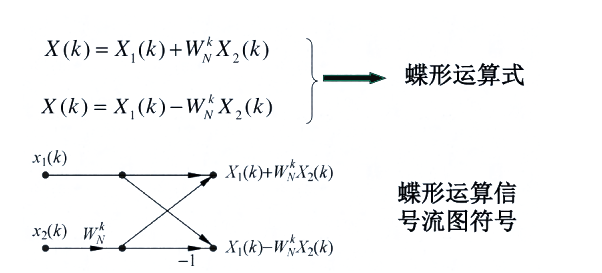
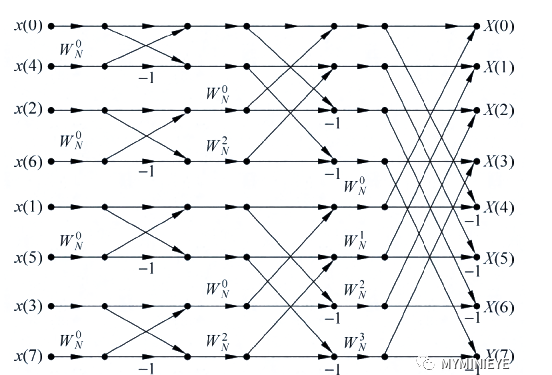
我们以8点的信号为例，三次按照奇偶分解，它的FFT信号流图如下：

 

 

2.抽样定理

抽样定理表明：如果一个连续信号f(t)，其最高截止频率为fm，如果用时间间隔为T≤1/(2*fm)的开关信号对f(t)进行时域抽样，则f(t)可以被样值信号唯一表示。即保证抽样频率fs≥2*fm，可以由抽样信号fs(t),恢复出原始信号f(t)。

 

 

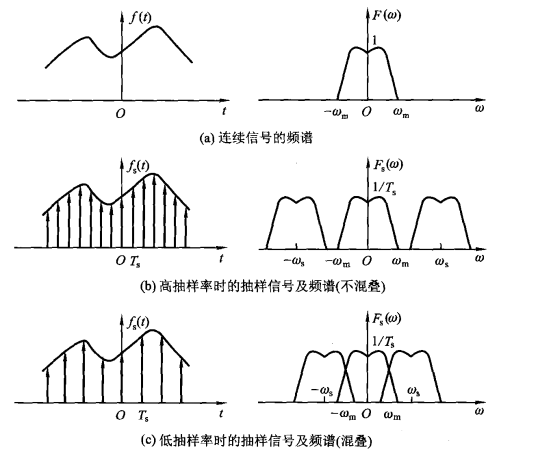
通常把最低允许的抽样频率f_s=2*f_m称为“奈奎斯特频率”，把最大允许的抽样间隔Ts=1/(2*fm)称为“奈奎斯特间隔”。

3.FFT频谱分析

因为FFT是基于复数的，在计算FFT的时候会出现两种情况，输入的数据为实数和复数，实际当中输入信号x(n)一般都为实信号，即虚部为零。

(1)输入数据是实数

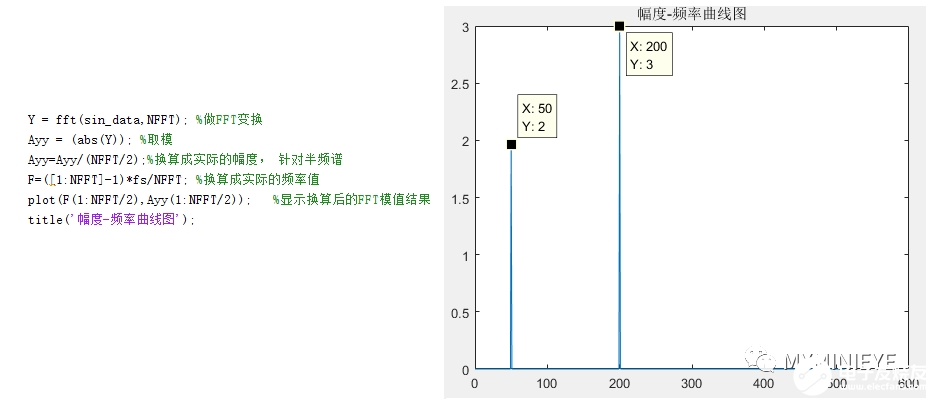
我们用matlab产生一个实正弦信号，如下：

 

 

正弦信号sin_data包含两个频点信号，f1=50Hz,f2=200Hz,采样频率fs=1024Hz，采样点数NFFT=1024，FFT之后结果为一个N点复数。每一个点对应着一个频率点，这个点的模值，就是该频率值下的幅度特性。所达到的频率分辨率为fd=fs/N=1024/1024=1Hz，某一点n所表示的频率为Fn=(n-1)*fs/N=n-1，每个点的模值是A的N/2倍，其中A为原始信号的峰值。FFT结果如下：

 

 

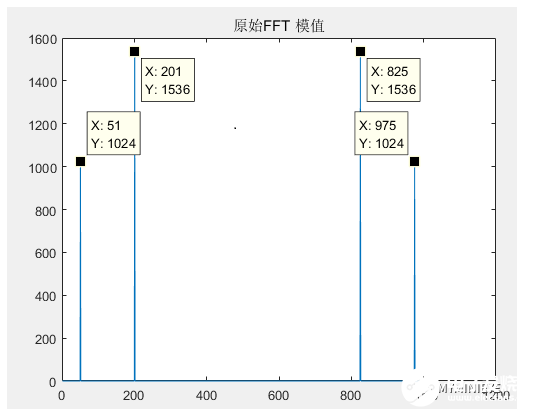
在频谱图中，前N/2个点有两个峰值，后N/2有两个峰值，是对称的。在上述中提到，FFT包含周期为2*pi的特性，在做FFT的时候得到的是[0,2*pi]，包含一个完整的区间。正频率分布在[0,N/2]与[0,2*pi]对应，N/2+1是正负频率的分界点，表示的频率为奈奎斯特采样频率的半，负频率分布在[N/2+1,N-1]与[pi,2*pi]相对应，[pi,2*pi]就等同于[-pi,0]，负频率没有物理意义，把上述频谱图做调整之后如下：

 

 

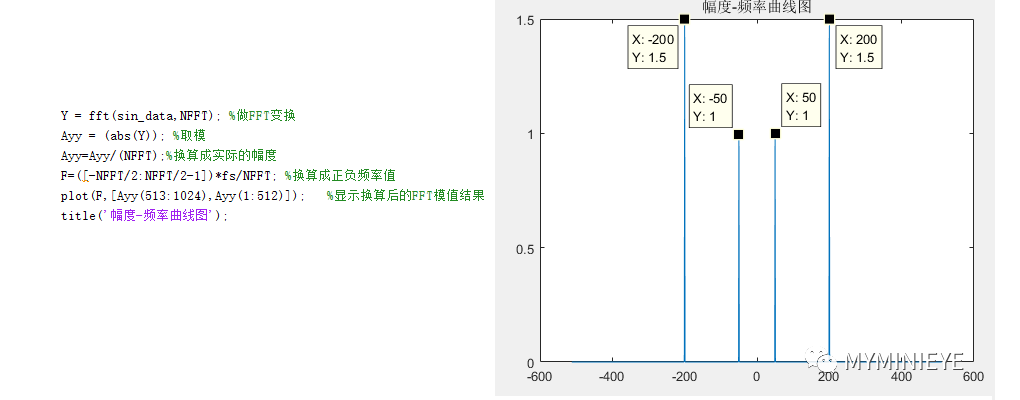
在做实数FFT时，往往将0~N/2点的值作为实际的频谱，由于正负频率幅值分量各占一半，幅值需要扩大2倍。

 

 

(2)输入数据是复数

我们用matlab产生一个和上述信号一样频率的复数信号，并观察其FFT之后的频谱，如下所示：

 

 

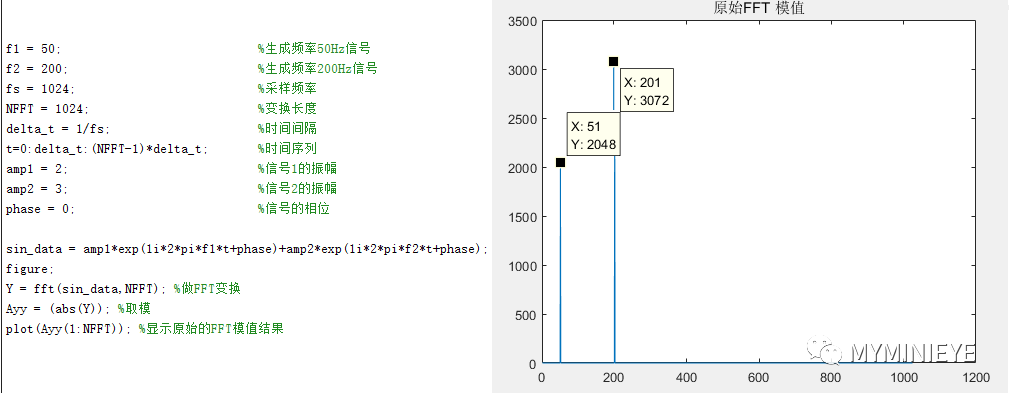
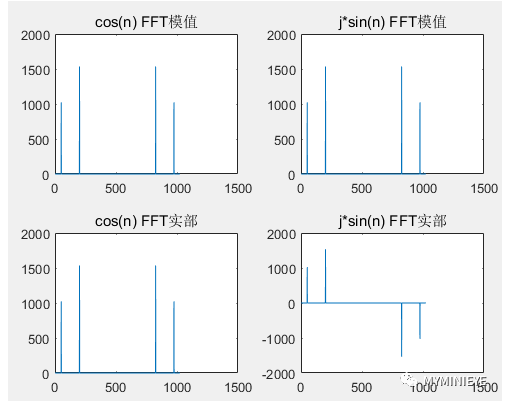
在做复数FFT的时候，只会有两个峰值，对应两个频率，且每个点的模值是A的N倍，A为原始信号的峰值。其实当我们输入指数形式的信号时，它包含实部和虚部两个信号，即x(n)=cos(n)+j*sin(n)。相当于是两个频谱的叠加，cos(n)产生一个频谱，j*sin(n)产生一个频谱，二者相互叠加，并不是没有了负频率，而是负频率相互抵消，正频率的幅值扩大了二倍。

 

 

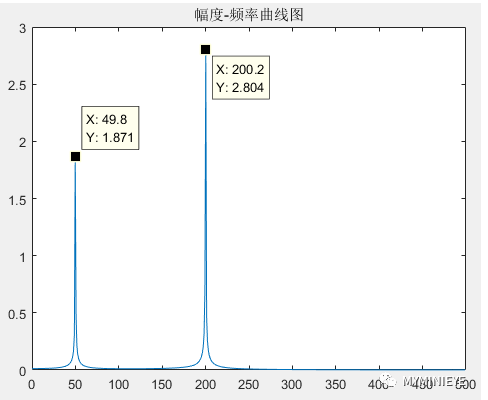
(3)在实际中，通过FFT计算得到频点信息往往和信号的频点信息不相同，会有误差，这就取决于频谱的分辨率，例如：当fs=1000Hz的时候fd=fs/N=1000/1024=0.97Hz，因为f1=50Hz,f2=200Hz不是fd的整数倍，所以FFT的频谱中不包含这两个频点，只有其周围相接近的整数倍频点，通过FFT得到的频谱如下：

 

 

4.频率分辨率

频率分辨率也叫做两个相邻谱峰分开的能力，指分辨两个不同频率信号的最小间隔。我们用matlab产生一个余弦波信号(频率分别为1MHz和1.05MHz)，幅值都为1，采样频率fs=100MHz，采样点数N=1000，对这1000个数据点做FFT得到频谱如下：

 

 

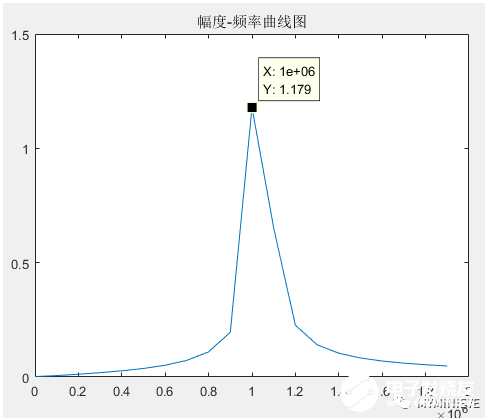
可以发现频谱点稀疏，在1MHz附近无法将1MHz和1.05 MHz的两个频率分开，频率成分无法被区分，一般由于频率分辨率不够造成的。

频率分辨率大致有两种类型，一种叫波形分辨率，由原始数据的时间长度决定：

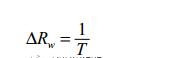
另一种叫视觉分辨率或FFT分辨率，由采样频率和参与FFT的数据点数决定：

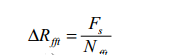
区分不同频率成分，是为了在数据点数不是以2为基数的整数次方是对原始数据进行“补零”操作。如果直接对原始数据做FFT，这两种频率分辨率是相等的。

(1)补零

现在对原始数据进行“补零”操作，在采样点1000个原始数据后面补充零达到7000个数据点，再对其做FFT，结果如下图所示：

 

 

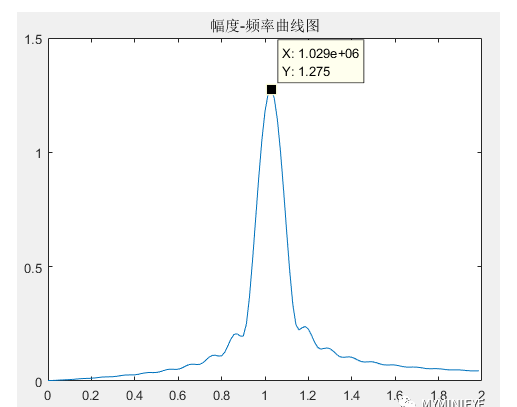
可以发现频谱点密集了很多，但是在1MHz附近仍无法将两个频率成分分开，所以，虽然我们补了很多的零，但是波形分辨率仍然为1/T1 = 100kHz,大于1MHz和1.05MHz这两个频率成分之间的距离50kHz。时域补零相当于频域插值，也就是说，补零操作增加了频域的插值点数，使得频域曲线看起来更加光滑，增加了FFT频率分辨率。

(2)增加数据时间长度

在采样频率不变的情况下，想要分辨这两个频率，必须要改变波形的分辨率，也就是延长原始数据的时间长度，现在我们以同样的采样频率对信号采7000个点作为原始信号，然后对齐做FFT，得到的结果如下:

 

 

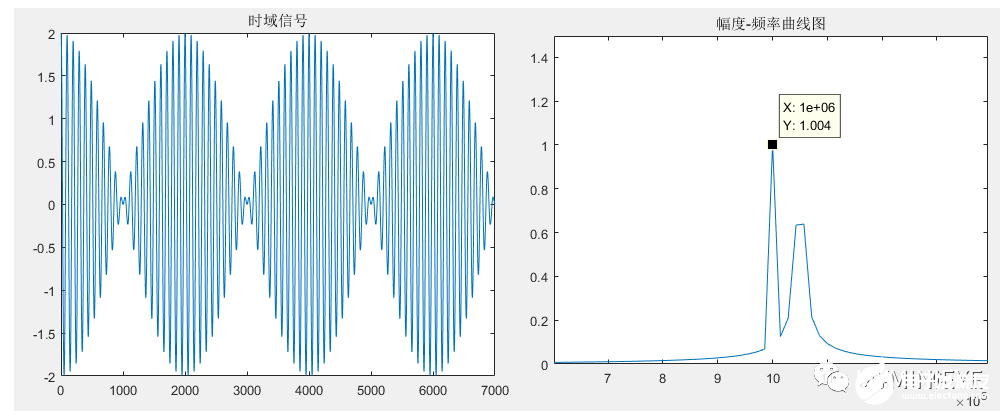
此时的波形分辨率为1/T2=14kHz，小于50KHz，可以看到有两个明显的峰值，但是会发现1MHz对应的幅值为1，与原信号中该频率成分的幅值一致，但1.05MHz对应的幅值明显低于1，这就是所谓的频谱泄露。使得在1MHz处有谱线存在，在1.05MHz处没有谱线存在，使测量结果偏离实际值，同时在实际频率点的能量分散到其它频率点上。

(3)为了解决这个问题，我们可以设法使得谱线同时经过1MHz和1.05MHz这两个频点，找到他们的最大公约数50kHz，用FFT分辨率计算得到FFT数据点数2000，但是我们的数据点已经有7000了，我们对点数扩大四倍到8000点，也就是补1000个零。这时FFT分辨率为12.5kHz，所以谱线同时经过1MHz和1.05MHz这两个频率点，对其做FFT结果如下：

 

 

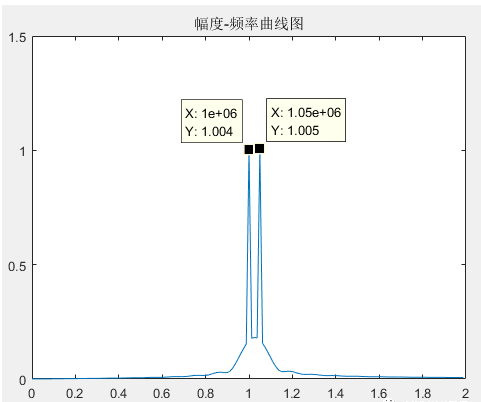
从上图中可以看到，两个频点的幅值均与原信号一致，这也是补零操作带来的影响。

编辑：hfy