关于LDPC编码的全面了解

一.LDPC编码介绍

1.为什么要用LDPC编码，LDPC编码相对其他编码的好处

LDPC(低密度奇偶检验)码是由稀疏校验矩阵定义的线性分组码，具有能够逼近香农极限的优良特性，其描述简单，具有较大的灵活性和较低的差错误码特性，可实现并行操作，译码复杂度低，适合硬件实现，吞吐量大，极具高速译码的潜力，在码长较长的情况下，仍然可以有效译码。

目前常用的信道编码体制有BCH码、RS码、卷积码、Turbo码和LDPC码等。其中BCH码和RS码都属于线性分组码的范畴，在较短和中等码长下具有良好的纠错性能；卷积码在编码过程中引入了寄存器，增加了码元之间的相关性，在相同复杂度下可以获得比线性分组码更高的编码增益；Turbo码采用并行级联递归的编码器结构，其分量采用系统的卷积码，能够在长码时逼近香农极限，同时译码复杂度也可以接收，但是它的译码复杂性仍然较大，且码长较长时，由于交织器的存在具有较大的时延。

相比之下LPDC具有以下特性：

(1)译码的复杂度很低，运算量不会因为码长的增加而急剧增加；

(2)采用迭代译码算法，可以实现并行操作，具有高速的译码能力；

(3)吞吐量大，从而改善系统的传输效率，并且便于硬件实现；

(4)译码复杂度与码长成线性关系，克服了分组码在长码时所面临的巨大译码计算复杂度的问题，使长编码分组的应用成为可能。

二.LDPC编码基础
1. LDPC编码的定义及矩阵表示
LDPC码是一类具有稀疏矩阵的线性分组码，在线性分组码中，任意两个码字的和仍属于这个分组码，输出的码字只和输入的信息位有关，即每个消息是独立编码的。

假设信源输出一系列的二进制0和1，这些二进制块分成固定长的消息块，每个消息块记作M，由k比特信息组成,其中M=[m0,m1,…m(k-1)]。然后根据一定的编码方式产生一个n维向量，这个向量就叫做m的码字，假设信息M对应的码字位C，其中C=[c0,c1,…c(n-1)]，则可以找到k个线性无关的码字g0,g1,…,g(k-1)，使得：

C= m0*g0+m1*g1+……+m(k-1)*g(k-1)

在C中，信息位不变，校验位附加在信息为之后，写成矩阵的形式就是：

C= M*G

G是k行n列的矩阵，又称为生成矩阵。

另外，可以由n-k个n维线性无关向量h0,h1,…h(n-k-1)生成C⊥(表示与C对应的零空间)。因此对于任意的i，hi*CT=0写成矩阵的形式就是H*CT=0。

H为(n-k)行n列的矩阵，通常被称为校验矩阵,用来判断码字是否合法。

2. LDPC码的Tanner图
LDPC编码可以用Tanner图来唯一确定，其和校验矩阵是完全等价的。Tanner图的顶点称为节点，分为变量节点和校验节点，每个变量节点与每个码字比特相对应，它对应校验矩阵的每一行，每个校验节点与每个校验方程相对应，它对应校验矩阵的每一列，变量节点和校验节点之间的连线称为沿，也代表校验矩阵中的1。例如校验矩阵H如下：

图1

用Tanner图来表示H矩阵如下：

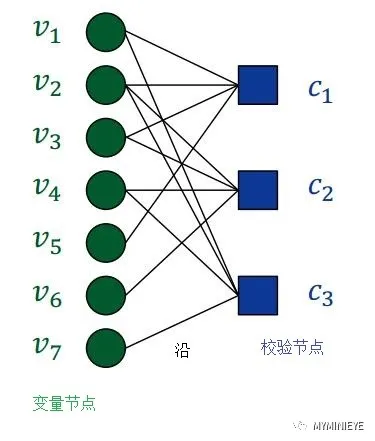
图2

在上图中，从节点v1出发，经节点c1,v2,c3，再回到v1，称为一个环，环的周长为该环所包含的边数，周长较短的环影响译码的性能，短环的存在会使得译码重复迭代，影响译码效率，使译码收敛速度变慢，在构造LDPC编码时应尽量避免出现短环。

3.eIRA编码算法
对LDPC码的编码可以采用线性分组码的通用编码方法，但通用编码方法的编码复杂度与码长的平方成正比，编码时延较大，实用性不强。eIRA(extended Irregular Repeat Accumulate，扩展的非规则重复累积码)编码算法，利用校验矩阵的稀疏性进行有效编码，使编码复杂度与码长成线性关系。

eIRA编码算法需要构造具有如下形式的校验矩阵

H=[H1 H2]

其中，H1是一个mXk维稀疏矩阵，H2是一个阶梯状下三角形矩阵，H2的形式如下：

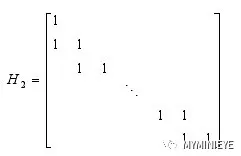
图3

系统码的生成矩阵形式为G=[I P]，其中I是单位矩阵 P=H1^TH2-T，H2^-T的形式为：

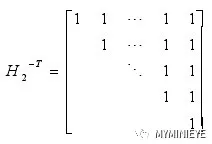
图4

H2^-T可以看成一个累加器，也称差分编码器。因此，eIRA 编码算法分两步进行，首先将待编码的信息矢量 m 乘以稀疏矩阵H1T，得到中间结果S，然后将中间结果S进行重复累加，得到校验比特，最后将信息比特和校验比特合并起来就得到最终的码字。

三.LPDC编码实现
1.LDPC编码过程
LDPC编码器的任务是将K个信息比特M=[m0,m1,…,m(k-1)]通过编码得到(N-K)个奇偶校验比特P=[p0,p1,…,p(n-k-1)]，最后得到的码字是将信息比特与校验比特合并，即得到码长为N的码字[i0,i1,…i(k-1),p0,p1,…,p(n-k-1)]。假设LDPC的码长位16200，码率为1/2，其中Nldpc = 16200,Kldpc =7200,Qldpc=25。

具体计算步骤如下：

(1)初始化p0=p1=p2=…=p(n-k-1)=0

(2)在表格中第一行指定的校验位地址处累加信息位i0,如下图所示，这一步的操作为编码的信息矢量i乘以稀疏矩阵H1^T，一共有20行，即360*20 = 7200。

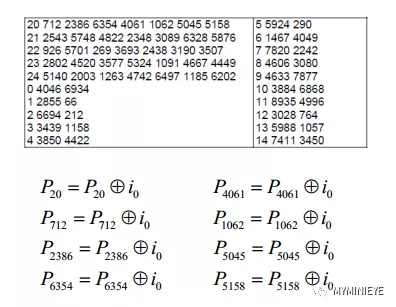
图5

对于接下来的359个信息位，im,m=1,2,…,359。在{x+(m mod 360) * Qldpc } mod(Nldpc-Kldpc)指定的校验位地址累加信息位im，其中x表示信息为i0对应的校验位地址。

(3)对于信息i1，校验位的地址需要根据 i0的地址来求，例如第一个校验位地址,{20+(1 mod 360) * 25 } mod (9000) = 45，第二个校验位{712+(1 mod 360) * 25} mod (9000) = 737，求出所有的校验位地址，然后进行信息累加，如下：

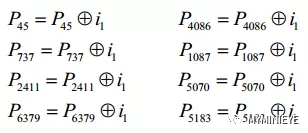
图6

(4)对于第361个信息位i360，在表中的第二行指定了累加器对应的校验位地址。和步骤3相同的处理方式，接下来的359个信息位对应的校验位地址为{x+(m mod 360) * Qldpc} mod (Nldpc-Kldpc)，其中x表示i360对应的校验位地址。

(5)以同样的方式处理每一组信息位，给出每一组对应的校验位地址。

(6)从i=1开始，按照下面的公式完成迭代计算

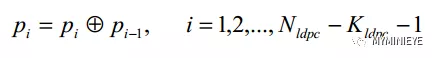
图7

2.matlab实现
在matlab中，有专门的函数来实现ldpc编码，但是在实现编码之前，需要我们产生一个我们需要的校验矩阵H。这里以Nldpc = 16200 ,码率1/2为例，介绍校验矩阵H的产生过程。

(1)按照上述LDPC编码中提到的，把校验位起始的地址存储起来，用于计算

其他的校验位。

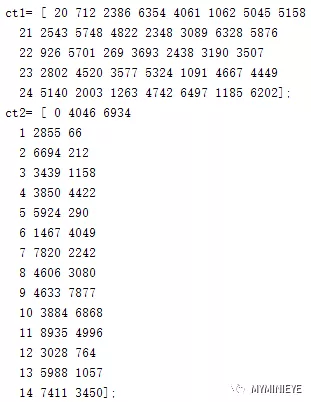
图8

把数据分成两组是因为数据的列数不一样，把相同列数的归到同一组里，这样更方便计算。

(2)根据公式，第一行，计算剩余359个校验位地址，其他行也做同样的操作，如下代码表示计算ct1所表示的校验位，ct2校验位的计算同ct1。

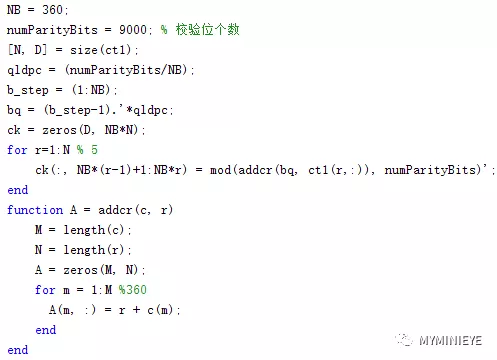
图9

(3)计算完所有的校验位之后，按照如下操作产生校验矩阵

图10

(4)用产生的校验矩阵，计算LDPC编码，这里使用comm.LDPCEncoder函数来实现，在较早的matlab版本中是fec.ldpcenc函数。

图11

3.FPGA实现
FGPA不可能一次性存储那么多的数据，并且也不现实，需要根据实时的计算产生校验位。通过上述的分析可知，LDPC码的编码具有周期为360的并行结构，如果把长度为K的信息比特分成r=K/360组，长度为N-K的校验比特分成s=(N-K)/360如下所示

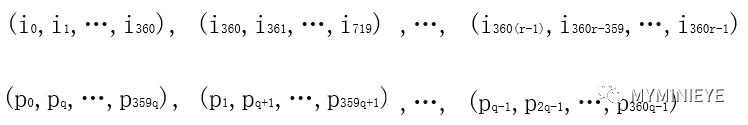
图12

由每个信息比特对应的校验比特公式pj=pj⊕im，其中j={x+(m mod 360)*q} mod(N-K)，x是第im个信息比特所对应的校验比特地址。可知,每一组信息比特均参与了同一组校验比特校验的过程。

考虑到码的周期性，我们可以同时进行M=360次并行处理，增加编码效率，可以写成以下迭代公式:

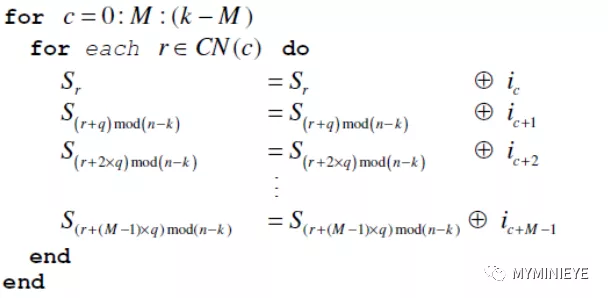
图13

其中符号‘r’和‘c’表示校验矩阵 H 的行和列，和信息节点连接的所有检验节点的集合定义为CN(c)。两个迭代循环，每次计算M个信息位，按照下面的矩阵形式存储Sr

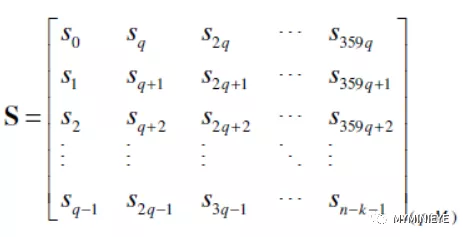
图14

从公式中可以看到，并行更新的M个Sr处于矩阵的同一行，但是输出的顺序并不是我们想要的顺序，不是从行的第一位到最后一位，因此需要对输入的信息位做循环移位，以保证S矩阵的结构。

一旦得到Sr就可以得到pr

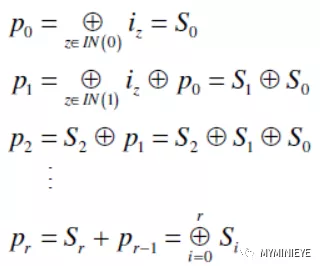
图15

计算S矩阵所有列的累加和，可以的到下面的向量

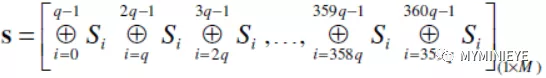
图16

然后按照下面的公式计算s’

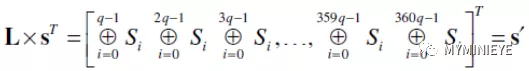
图17

其中，L位MXM的下三角矩阵，然后将s’逻辑右移一位，得到

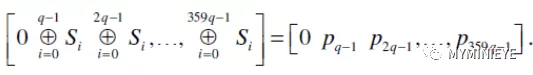
图18

最后按照下面的公式，每次计算Mbit校验位

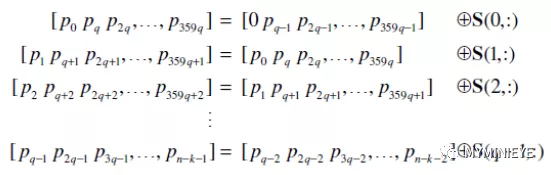
图19

根据以上的公式推导，提出以下的实现结构，有三个主要部分组成：第一部分计算Sr的值，第二部分就算S矩阵中列的累加和，第三部分计算校验位。编码器的系统结构主要包括编码配置模块(Ldpc_contrl)，信息位分组计数模块(data_recv)，基地址产生模块(Bom_addr)，数据地址计算模块(ADDER_GEN)，校验位计算模块(iterator)，整个系统结构如下图所示：

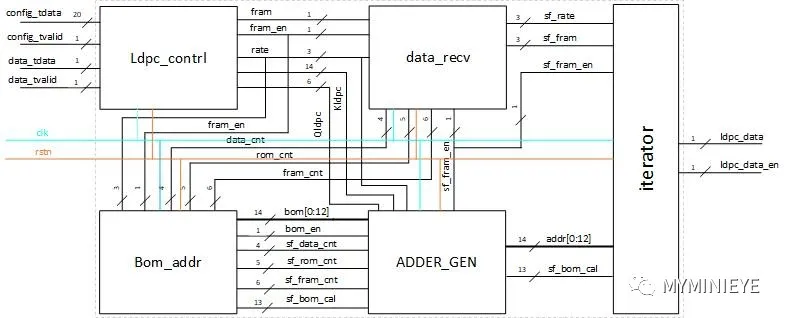
图20

3.1编码配置

在配置模块中提供了1/4，1/2，3/5，2/3，3/4，4/5，5/6七种码率，为了实现编码方式的可配置，利用寄存器保存不同码率下的参数，主要包括Qldpc,Kldpc，可以在整个系统结构中看到。首先检测配置使能信号，然后加载配置数据，保存参数。其中fram和fram_en是输入信息位和使能延迟输出，考虑到最坏的情况下，配置信号和数据同时到来，需要先配置，才能进行数据的处理，所以对数据要延迟几个时钟周期。

3.2 信息位分组计数

模块的主要作用是对输入的信息比特进行序号标记，采用三个计数器，其中data_cnt为 0~14 表示15个数据 rom_cnt 为 0~23，24组表示共24*15=360个数据，0表示初始数据，fram_cnt，360bit的组数统计。如对应1/2码率，输入数据为7200bit，则数据可分为：20*360 = 20*15*24 =7200，下图为信息位分组计数模块主要信号的时序图，延迟的是因为在计算校验位地址的时候会花费时间，为了后边计算校验位时信息位能够和校验地址对齐。

图21

3.3 基地址产生

基地址产生模块根据输入的码率选择存在rom中的基地址，选择基地址的读取位置由输入的码率和输入序号共同确定，输入码率确定及地址的起始位置，序号fram_cnt确定基地址的偏移。以1/2码率为例，rom中初始地址为63，当fram为0时表示第一行，读取的基地址如下：

图22

仿真时钟周期为20ns，地址输出相对信息位使能延迟了16个时钟周期，其中移位输出的计数器分别延时了两个时钟周期。延迟是为了在校验位计算的时候，地址能够和信息位对齐。

3.4 数据地址计算

地址计算模块需要根据公式{x+(m mod360) * Qldpc } mod (Nldpc-Kldpc)，计算每个信息位所对应的校验位。但是这个公式所用的取模以及乘法运算不适合在FPGA中运算，会占用很多的DSP资源，而且也是不必要的。以1/2码率为例，可以转化为如下的加减运算。

图23

result = Amod B ，当A小于B时result等于A本身，当A大于B时result等于A-B，通过这个模块计算出每个信息位所对应的的校验位。

图24

其中data_in_bom为初始地址，data_in_addr为计算的校验位地址。

3.5校验比特计算

校验比特计算需要完成两个部分，第一部分为信息位的输出，第二部分为校验位的输出。因为在硬件中为实时处理。以1/2码率为例，发送的16200bit码字，包括7200bit信息位，9000bit校验位，两个部分分时段进行。系统采用13个并行度计算校验位，其中的一个的时序如下：

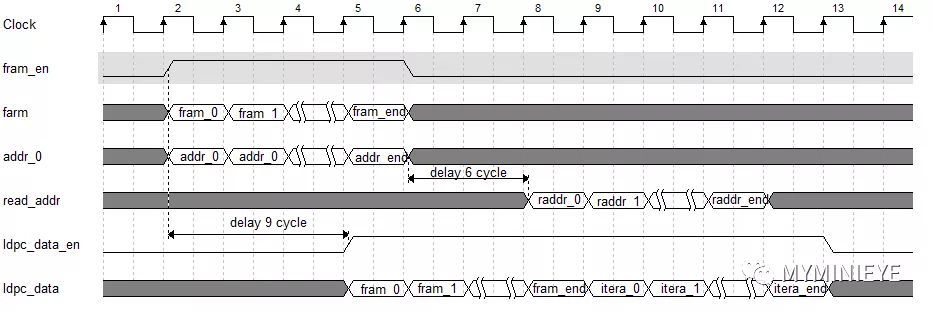
图25

双口ram设置为read first，数据相对于地址有三个时钟的延迟。上述中所涉及的延迟均在调试中根据运算所需时钟数进行的延迟。采用13个并行度计算校验位，其中的一个的结构如下，addr_ena和addr_flag均由read_addr控制。

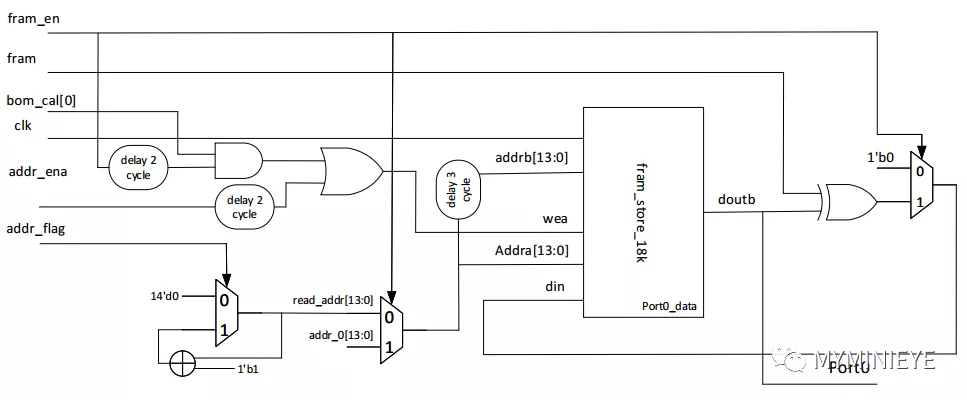
图26

最后把每个13个并行度的数据相加，然后与上一位的值异或，得到最终的输出。

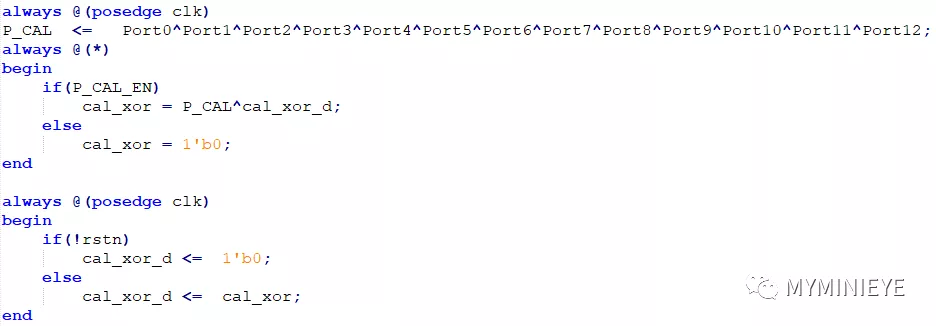
图27

通过modelsim把结果输出和matlab计算的结果进行比较，可以看到我们使用FPGA实现的结果和用matlab做出的结果是一样的。

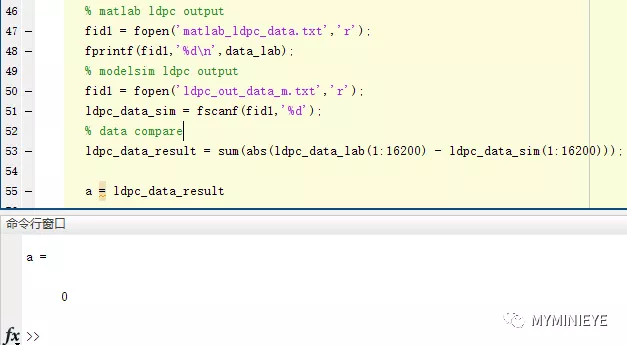
图28

编辑：hfy