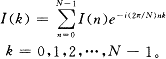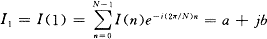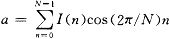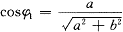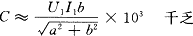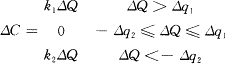高压无功功率自动检测补偿系统
电源设计应用
描述
高压无功功率自动检测补偿系统
在大型电力电子装置的供电系统中,往往存在着大量的谐波干扰,致使功率因数 难以测量、无功功率不易补偿。为此,本文提出了一 种新的高压无功功率自动检测补偿系统。通过对电流波形进行数字滤波,准确地确定了功率因数。同时,采用非线性控制技术,较好地解决了无功功率的自动补偿问题。试验证明,该系统稳定可靠,节能效果明显。
【关键词】 无功补偿,功率因数检测,数字滤波,非线性控制
AUTOMATIC MEASUREMENT AND COMPENSATION SYSTEM OF HIGH VOLTAGE REACTIVE POWER
XU Jun REN Yongyi
(National University of Defence Technology,Changsha,410073)
【Abstract】 There are a lot of harmonic disturbances in the power supply system of large-scale power electronics setup.The harmonic disturbances result in difficulties to measure the power factor and to compensate the reactive power.This paper presents a new automatic measurement and compensation system of high voltage reactive power.The power factor can be measured accurately by digital filter of current waveforms and the reactive power can be compensated by non-linear control.Experiments have proved that the system is stable and reliable.
【Keywords】 reactive power compensation,power factor measurment,digital filter,non-linear control
1 引言
在一般的供电系统中,若负载是线性的,则电流电压波形均为正弦。此时,功率因数的定义是电流电压间相位差的余弦。因此,一般的功率因数检测方法是,检测电流与电压信号过零的时间差,算出相应的功率因数角和功率因数。但是,随着工业的发展,电网中的谐波日趋严重。特别在一些大型电力电子装置(如:电弧炼钢炉等)的供电系统中,负荷的非线性和冲击性等常会产生大量的高次谐波,使供电电流波形产生明显畸变。此时,上述确定功率因数的方法将不再合适,并由此导致按常规算法得到的无功功率也不准确,进而使无功自动补偿的效果变差。为此,本系统提出并采用了数字滤波的方法,提取畸变电流波形的有效分量,得到相应的功率因数值。同时,针对相位补偿调节器的特点,利用非线性控制技术较好地实现了无功功率的自动补偿。
2 系统的工作原理
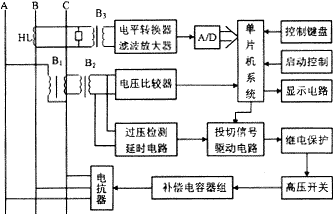
系统的原理框图如图1所示。
|
图1 系统原理框图 三相高压电的AC相高压经电压互感器B1和降压变压器B2加入电压比较器,得到一频率为50Hz的矩形波。将该矩形波输入至单片机,作为对电流信号采样的启动信号。B相电流经电流互感器HL和隔离变压器B3加至滤波放大和电平转换电路。其中,滤波放大电路一方面将电流信号放大到合适的幅度,另一方面则对电流信号中可能引起频率混叠的高次谐波进行初步抑制,以利提高后续数字滤波的精度,滤波器的截止频率应为基波频率的N/2倍。本系统每周期的采样点数为64,故滤波放大电路的截止频率取为1600Hz。这样既可满足采样定理的要求,又使滤波器本身产生的相移相对功率因数角可以忽略,减少系统附加相移造成的影响。 3 滤波与控制算法 为确定合适的滤波与控制算法,首先应对畸变电流的谐波含有率和非正弦电路中无功功率与功率因数的定义及算法进行研究。以在株洲钢厂110kV/6kV变电站测得的两台电弧炼钢炉不同冶炼期的电流信号为例,采用FFT进行频谱分析,算出电流信号的平均谐波含有率如表1所示。 表1 电弧炉的平均谐波含有率(%) |
| 谐波次数 | 谐波含有率 | 谐波次数 | 谐波含有率 |
| 1 | 100 | 11 | 1.73 |
| 2 | 11.65 | 12 | 4.83 |
| 3 | 10.85 | 13 | 1.78 |
| 4 | 4.29 | 14 | 2.42 |
| 5 | 13.28 | 15 | 0.24 |
| 6 | 3.94 | 16 | 0.69 |
| 7 | 3.65 | 17 | 0.93 |
| 8 | 1.67 | 18 | 0.31 |
| 9 | 3.51 | 19 | 0.68 |
| 10 | 2.57 | 20 | 0.34 |
|
有功功率 cos 因此,只要得到电压、电流的基波分量U1和I1及其夹角的余弦cos
令k=1可得电流信号的基波分量:
其中,实部
虚部
则基波功率因数为:
由此不仅可以得到系统的功率因数cos
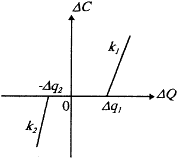
实际中,当电流波形畸变且冲击性较大时,补偿电容的容量还不能简单地按上式计算。因为,幅值和相位经常变化的电流信号会造成补偿电容器的频繁投切,从而影响高压真空开关的寿命。为此,本系统设计了相应的非线性数字PI调节器,其非线性特性如图2所示。 |
|
图2 调节器非线性特性 图中ΔQ为本次采样检测所得的无功功率与前次无功功率之差值,ΔC则是应增加或减少的补偿电容容量。
其中,Δq1和k1分别是无功功率为正,即无功是感性时的投切门限和调节器比例系数;Δq2和k2则是无功功率为负,即无功是容性时的投切门限和调节器比例系数。由于电业部门对无功为负控制很严,故必须要求:Δq2<Δq1,k2>k1。 C(n)=C(n-1)+ΔC(n) 总之,系统在硬件复位后即开始运行数字滤波和非线性控制算法。首先对电流信号做DFT处理,算出系统的功率因数和无功功率。然后,针对无功功率的大小和符号进行非线性PI调节运算。当无功大于投切门限[-Δq2,Δq1]时,分别按感性无功或容性无功的比例系数(k1、k2)做PI调节运算,输出相应的投切控制量;而当无功小于投切门限时,则保持原输出投切量不变。在这里Δq1、Δq2、k1和k2的设置不仅可凭经验由程序给定,而且可根据实际情况通过一个4×4小控制键盘改变。这大大增加了系统的适应性,为用户提供了更多的方便。 4 试验与结论 本系统研制成功后,分别在实验室和现场环境对不同相位的工频信号进行了功率因数的检测精度试验。结果表明,系统功率因数检测的平均误差小于2%。之后,全系统在株洲钢厂110kV/6kV变电站投入实际运行,表2给出了系统运行前后变电站功率因数的变化情况。 表2 系统运行前后变电站功率因数变化情况 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 平均 | |
| 补偿前 | 0.84 | 0.83 | 0.86 | 0.80 | 0.82 | 0.85 | 0.83 | 0.81 | 0.83 | 0.83 |
| 补偿后 | 0.98 | 0.90 | 0.95 | 0.95 | 0.97 | 0.98 | 0.95 | 0.95 | 0.96 | 0.95 |
|
作者单位:国防科技大学,长沙 410073 参考文献 1 宋文南等.电力系统谐波分析.北京:水利电力出版社,1995 |
- 相关推荐
- 自动检
-
电网无功功率补偿控制系统的设计2009-11-01 1197
-
电容器补偿过高无功功率会变大吗?2023-09-08 1512
-
净化型无功功率补偿稳压器的意义2013-08-09 0
-
有关无功功率补偿的2017-05-15 0
-
雷达故障自动检测系统2009-07-15 584
-
霍尔电流传感器在电网无功功率自动补偿中的应用2009-03-06 1072
-
无功功率动态跟踪补偿装置2009-07-10 1046
-
无功功率补偿介绍2011-12-21 2453
-
谐波抑制和无功功率补偿2017-02-07 1341
-
无功功率补偿原理_无功功率补偿的方法2019-06-27 12038
-
什么是无功功率?无功补偿的作用和原理2023-08-16 2029
-
提高功率因数进行无功功率补偿有什么意义?无功补偿有哪些方法?2024-01-22 1351
-
无功功率自动补偿器不工作的原因2024-03-13 1380
-
无功补偿器怎么调到自动补偿2024-04-24 958
-
无功功率补偿器显示欠电流的原因2024-11-06 829
全部0条评论

快来发表一下你的评论吧 !

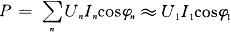
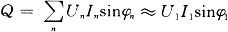
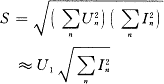
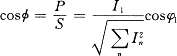
 只是一种习惯的表示方法。当电流的 谐波含有率取表1提供的数据时
只是一种习惯的表示方法。当电流的 谐波含有率取表1提供的数据时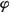 1
1