预测控制中的稳态优化策略

预测控制中的稳态优化策略

    摘  要：预测控制算法为了在自由度不足时按优先级优先保证基本控制目标，在自由度多余时充分利用自由度提高效益，在算法中引入了优化+控制的策略。本文首先介绍和分析了以前对预测控制的改进工作，最后给出了基于目标规划思想的优化策略。
    关键词：预测控制  稳态优化  目标规划

1 引言
    预测控制算法除了可以处理约束外，吸引工程人员的另一个优点在于：作为一个多变量控制算法，预测控制中的系统输入并不是仅仅和某一个特定的输出关联，所有的被控变量在一个体系之中。这样就可以在系统由于输入饱和、执行机构失灵等原因造成自由度丢失后，仍可以寻找最佳控制效果，保证装置的平稳运行；另外如果存在多余的自由度，即在满足控制要求的同时操纵变量可以在一定的范围变化，这样预测控制可以在更加经济的状态运行。但是传统的控制策略不能够实现上面的要求。
    为了发挥预测控制的优点，实现上面要求，需要引入新的策略。优化+控制策略是其中比较成功的策略之一，在优化层完成控制层的设定值计算，这一计算包括：按优先级首先确保重点控制目标，然后是一般控制目标，最后如果仍存在多余自由度，则在保证前面控制目标的前提下进行经济优化。
    本文在对以前所做工作进行分析后，提出了基于目标规划理论的优化策略，这种优化策略和传统的算法相结合可以高效、简洁地达到上面的目的。
2 以前的工作
    对R维输入、S维输出的系统，预测控制算法总是试图求解未来M个时刻(控制时域)的控制，使模型预测输出在未来P个时刻(优化时域)内达到以上基本目标。最初的动态矩阵控制(DMC)可以描述如下［１］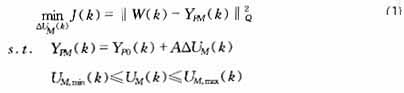

        (还包括一些其它变量，如被控变量、操纵变量的约束条件)     (2)
    其中，W(k)为参考轨迹，(S×P)维向量；YPM(k)为ΔUM（k)作用下模型预测输出，(S×P)维向量；YP0(k)输出预测初值，(S×P)维向量；A为动态矩阵，由阶跃响应系数排成的(S×P)×(R×M)维矩阵；Q=block-diag(Q1，…，Qs)，Qi=diag［qi(1),…,q?i(p)］,i=1,…,S。
    预测控制器的操纵变量多于被控变量时，操纵变量可能存在多余的自由度。充分利用多余自由度，预测控制可以在更经济的状态下运行。为了利用多余自由度，需要在控制目标中引入和经济效益相关的变量，这些变量称为经济变量，可以归结为控制量的稳态目标，如让控制量尽量接近其理想稳态值(Ideal Rest Value-IRV)。
    基于这样的思路将反映稳态优化要求的项加入到性能指标(1)中，就可以得到一种称为综合性能指标法的预测控制改进方法：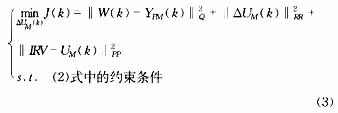


    但综合性能指标法也存在缺点，具体如下［２］：（1)存在大的阶跃扰动时，由于目标函数可能增加太快造成控制作用被抑制，使控制作用迟缓，输出响应偏差大和回复时间长；（2)采用综合指标法的控制系统一定是瘦系统，当存在模型失配和扰动时，设定值yset。和uset不可能同时实现。由于在实际中，模型失配和扰动的存在不可避免，这样将造成稳态余差。

    其中等式约束中的YP′M′(k)是从未来P个时刻预测值中选出的。
    由于采用了分层优化的合理结构，多目标优化方法克服了综合目标法的一些不足，但是这种方法对自由度减少和如何根据优先级，实现对主要控制目标的优先控制没有涉及。这主要是由于改进算法把重点放在了如何利用“胖系统”的多余自由度上，没有过多考虑“瘦系统”自由度不足时的情况。
    Swartz［４］针对“瘦系统”自由度不足的情况，提出了分层监督控制策略，在监督控制中根据优先级，实现被控输出设定值的优化计算。设定值通过根据优先级定义的优化子问题序列取得，其中每一个子问题都是一个二次规划，其目标函数为尽可能使输出设定值接近期望值而且在上一级优化子问题的约束，实现在保证上一级优化控制目标的前提下，进行优先级低的优化问题的求解。这种方法的优点：确保控制效果，采用分层的优化+控制结构。这种方法的缺点主要在于多级的二次规划求解计算量太大，另外稳态经济指标不能直接放入优化问题中，这样在存在多余自由度的情况下，经济目标的优化还需要其它工作。
        Swartz的监督控制策略中计算的是稳态时的输出设定值，而经济指标也是稳态优化，所以我们结合上面所做的工作，提出了一种新的优化+控制的两级预测控制算法，同时实现稳态优化和动态控制。在优化部分使用简单的目标规划方法，提出了包括被控输出设定值计算和经济指标优化的稳态优化测量，在动态控制部分吸取综合指标法的优点，增加了对稳态经济目标的控制而且克服了综合指标法的缺点。这种采用线性规划进行局部优化、预测控制进行动态控制的算法，可以实现所谓胖瘦系统的自由转换，在优先保证基本控制目标的前提下，实现经济目标优化。
    总的来看，以前的工作都有可取之处，但是考虑的问题具有局限性，不是仅仅考虑了多自由度下的稳态经济指标优化，就是仅仅考虑了自由度不足时基本控制目标的优先级控制。相比较而言，本文提出的改进的优化+控制策略可以实现胖瘦系统的自由转变，而且在按优先级保证控制目标的前提下，追求经济目标的最大化。
3 基于目标规划的优化策略
    被控对象的线性稳态模型描述如下：
  ?Ｙ＝ＧＵ＋δ    (4)
中G为稳态增益矩阵，δ是阶跃扰动对输出影响的估计。
    δ提供了一种克服不可测扰动和模型失配影响的反馈机制，扰动估计可以采用?Cutler提出的方法，对于SISO系统：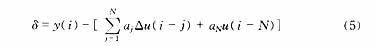

    其中y(i)表示当前测量值，u和Δu分别为括号内采样时刻的输入和输入变化，ai是单位阶跃响应系数，N是系统的模型时域。假设扰动为阶跃扰动。
    对于式(1)描述的系统，稳态优化的任务是根据约束和工程人员或者上一层优化给出的控制要求和期望的经济指标，计算预测控制中的设定值。
    目标规划［５］的目标函数是按各目标约束的正、负偏离变量和赋予相应的优先级系数而构造的，当每一个目标值确定以后，优化的要求是尽可能靠近目标值。优先级需要根据实际情况给出，设共有k个优先级，优先级系数Pi(i=1,2，…，k)满足P1>>P2>>…，>>Pk。一般基本控制目标比经济目标的优先级高主要控制目标比次要控制目标的优先级高。在实际应用中优先级系数只要保证优先级可以得到体现即可。
    如果是设定值优化那么目标函数是minz=f(d+,d-)，如果是不大于某一个区间上限则目标函数为minz=f(d＋)，如果是不小于某一个区间下限则目标函数为minz=f(d－)，如果是区间则控制目标为上面两种情况的综合。其中正偏差d＋表示决策值超过目标值的部分，负偏差d－表示决策值未达到目标值的部分，相关的d+、d-必定至少一个等于０。下面结合一个实例来说明基于目标规划的稳态优化策略。
    例1［６］过程是由三个产品抽出和三个回流组成的重油分馏塔，塔底回流温度是操作约束。操纵变量是塔顶和侧线的抽出以及塔底的回流量。塔顶回流用来和其它装置换热，可以认为是可测扰动。4个输出包括u3的理想稳态值，输出输入变量如表1。
    使用稳态增益并设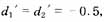那么稳态模型如式(3)描述，其中

    定义稳态优化目标以及优先级如表2

优化目标中-0．5＜y3属于区间优化，y1＝0，y2=0属于设定值优化，y4=0．5属于经济量的ESV。
硬约束为：－0．5≤y1≤0．5；－0．5≤ui≤0．5，i=1,2,3
这一优化问题的目标规划如下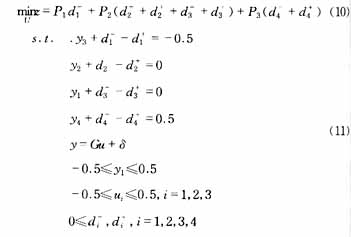

    计算结果控制作用为ul=0．5，u2=-0．0529，u3=-0．104。利用控制作用可以得到输出的设定值yl=０、y2=0、y3=0．0076、y4=-0．104。也就是说预测控制中的设定值将从这几个数据中产生。这样的设定值是合理的，所以预测控制可以无偏的实现并且保证较快的回复时间。
    为了验证目标规划算法，假设前3个高优先级满足那么这个问题可以用如下的线性规划表示

    线性规划的结果是-0．104，这也说明了目标规划的正确性。如果有多余的自由度目标规划也会把第4优化级优化到目标值，但是现在由于没有多余的自由度，所以目标规划就只有使第4优化级尽量接近目标值。
    例2

    情况1，当ytgt=5，IRV=0，解上述目标规划可以得到动态控制的设定值为y=5；u2=0
    情况2，当ytgt=10，IRV=0，解上述目标规划，由于ytgt=10的优先级高，所以首先满足它，然后尽量减少u2的负偏差，结果为ul=3，u2=2。可以得到动态控制的设定值为y=5；u2=2。所谓胖瘦系统的转变可以通过优化层变化控制层的设定值自然地得到体现。实际上由于没有自由度，此时的经济量为自然响应。
    情况3，当ytgt=15，IRV=0，解上述目标规划，可以得到动态控制的设定值为y=12；u2=3。即使自由度用尽也不能够满足基本控制目标。
    情况4，当8≤ytgt≤10,IRV=0，经计算设定值为y=8；u2=1。y=8是为了在满足区间的同时使经济目标尽量接近IRV。
4 结论
    预测控制器的动态控制用于克服扰动保证最佳工作点和在最佳工作点变化后移动工作点，实现了控制器的调节特性和伺服特性。预测控制器的稳态优化则实时的根据扰动和工况的变化寻找最佳工作点，预测控制器中的稳态优化可以使预测控制器克服以前存在的缺点更平稳高效的运行。本文首先介绍了预测控制器的特点和以前所做的工作，最后给出了基于目标规划理论的稳态优化策略。这种策略克服了传统预测控制存在的不足，可在自由度不足时优先保证基本控制目标，在自由度多余时充分利用自由度提高效益，而且由于采用的线性规划理论所以计算量不大。

参考文献：

［１］肖明波，钱积新．预测控制中静态目标的实现［Ｊ］．控制理论与应用，14(3)：313－317，1997
［２］Chao-Ming,srikanth Voorakaranam，Babu Joseph．Analysis and Performance of the LP-MPC and QP-MPC Cascade Control System［Ｃ］． Proceedings of the　ACC,Philadelphia,Pennsylvania．1998
［３］Grosdidier G.Froisy B．Hammann M.，The　IDCOM-M controller．IFAC Modelsbased predictive　process control［Ｃ］,1988，31－36
［４］C,L.E.Swartz,An algorithm for hierarchical supervisory control［Ｃ］．computers chem.eng.10(11):1173-1180(1995)