基于运算放大器的模拟积分器电路设计

在电子世界走向数字化之前，基于微分方程求解的控制系统使用模拟计算来解方程。因此，模拟计算机相当普遍，因为几乎所有微分方程的求解都需要对信号进行积分运算的能力。

虽然控制系统大多都已实现数字化，并且数值积分也已取代模拟积分，但在传感器、信号生成和滤波的运算方面，仍然需要模拟积分器电路。

这些应用使用基于运算放大器的积分器，并在反馈回路中带有电容元件，以便为低功耗应用提供必要的信号处理。尽管实用性仍然很重要，但许多设计人员可能会轻易忽略。

本文概述了积分器电路，并以 Texas Instruments 的几个产品为例，就正确设计、元器件选择和最佳实践提供指导，以实现卓越性能。

一、基本反相积分器

经典的模拟积分器采用运算放大器，并且以电容器作为反馈元件(图 1)。

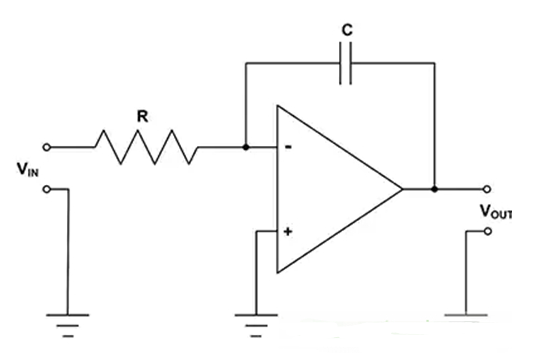
图 1：基本反相模拟积分器包含一个运算放大器，并且在反馈路径上有一个电容器。

积分器的输出电压 VOUT 是输入电压 V IN 的函数，可以使用公式 1 计算。

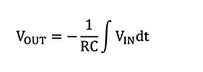
基本反相积分器的增益系数是 -1/RC，该系数可应用到输入电压积分。实际上，积分器所用的电容器应具有小于 5% 的容差和低温度漂移。聚酯电容器是一个不错的选择。在关键路径位置应使用公差为 ±0.1% 的电阻器。

该电路存在局限性，因为在直流下，电容器代表开路，增益会无穷大。在工作电路中，根据非零直流输入的极性，输出将传输到正电源轨或负电源轨。这可以通过限制积分器的直流增益来纠正(图 2)。

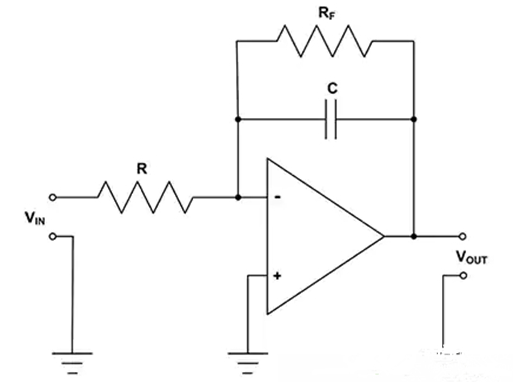
图 2：在反馈电容器上并联一个大电阻可限制直流增益，从而得到一个实用的积分器。

在反馈电容器上并联一个高阻值电阻器 (RF)，可将基本积分器的直流增益限制为 -RF/R 值，从而得到一个实用的器件。这种添加法解决了直流增益问题，但却限制了积分器的工作频率范围。观察真实电路有助于理解此限制(图 3)。

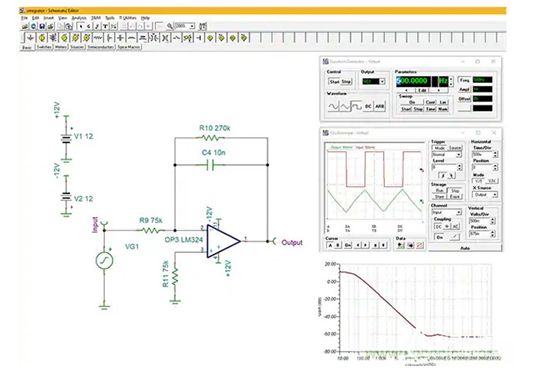
图 3：使用真实元器件的实用积分器 TINA-TI 仿真。

该电路使用 Texas Instruments 的 LM324 运算放大器。LM324 是一款优异的通用运算放大器，具有低输入偏置电流(典型值 45 nA)、低失调电压(典型值 2 mV)和 1.2 MHz 的增益带宽积。电路输入由仿真器的函数发生器以 500 Hz 的方波驱动。这在仿真器示波器上显示为上方迹线。电路会对方波进行积分，并输出一个 500 Hz 的三角函数，如示波器的下方迹线所示。

直流增益为 -270 kΩ/75 kΩ 或 -3.6 或 11 dB;这从电路的传递函数可以看出，如图 3 的右下网格所示。从约 100 Hz 至约 250 kHz，频率响应按 -20 dB/ 十倍频程滚降。这是积分器工作的有用频率范围，并且与运算放大器增益带宽积有关。

Texas Instruments 的 TLV9002 是新近推出的运算放大器。这款 1 MHz 增益带宽放大器具有 ±0.4 mV 的输入失调电压和 5 pA 的极低偏置电流。作为一款 CMOS 放大器，它适用于各种低成本便携式应用。

对于设计人员来说，务必要记住，积分器是一种累积器件。因此，如果没有适当的补偿，输入偏置电流和输入失调电压会导致电容器电压随着时间的推移而增加或减少。在此应用中，输入偏置电流和失调电压相对较低，并且输入电压会迫使反馈电容器定期放电。

在使用累积功能的应用中，例如在测量电荷时，在积分器中必须有一种机制来重置电压并建立初始条件。Texas Instruments 的 ACF2101BU 就具有这种机制。它是一款双开关积分器，集成了一个内置开关以对反馈电容器放电。由于该器件适用于需要电荷累积的应用，因此具有 100 fA 的极低偏置电流，典型偏置电压为 ±0.5 mV。

Texas Instruments 的 IVC102U 是一款类似的开关积分器 / 跨阻放大器。该器件与 ACF2101BU 的应用范围相同，但不同的是，每个封装包含单个器件。此外，还具有三个内部反馈电容器。其中包含对电容器组放电和连接输入源的开关，因此设计人员能够控制积分周期并包括保持操作，以及对电容器上的电压放电。

二、非反相积分器

基本积分器将信号的积分反相。虽然与基本积分器串联的第二个反相运算放大器可以恢复原来的相位，但也可以在单级中设计一个非反相积分器(图 4)。

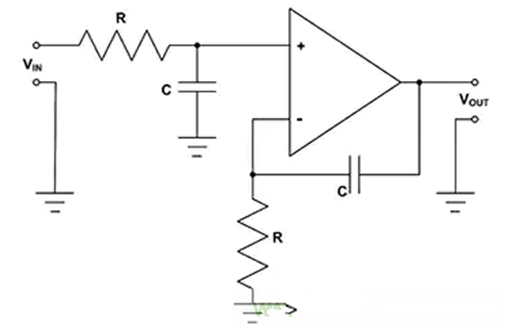
图 4：基于差分放大器运算放大器配置的非反相积分器可以确保输出相位与输入相位匹配。

非反相版本的积分器使用差分积分器来保持输出与输入信号同相位。这种设计额外增加了无源元器件，应对其进行匹配以实现最佳性能。输入和输出电压之间的关系与基本积分器相同，只是符号不同，如公式 2 所示：

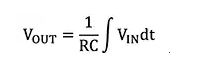
通过使用传统的运算放大器电路，可以实现对基本积分器进行其他调整。例如，可以添加多个电压输入(V1、V2、V3…)，只要通过各自的输入电阻(即 R1、R2、R3…)加到运算放大器的非反相输入。

输出是输入之和的积分。

三、一些常见的积分器应用

过去，积分器一直用于微分方程求解。例如，机械加速度是其速度的变化率或导数。速度是位移的导数。积分器可用于获取加速计的输出并对其进行一次积分运算，以读取速度。如果速度信号进行了积分运算，则输出就是位移。这意味着通过使用积分器，单个传感器的输出可产生三个不同的信号：加速度、速度和位移(图 5)。

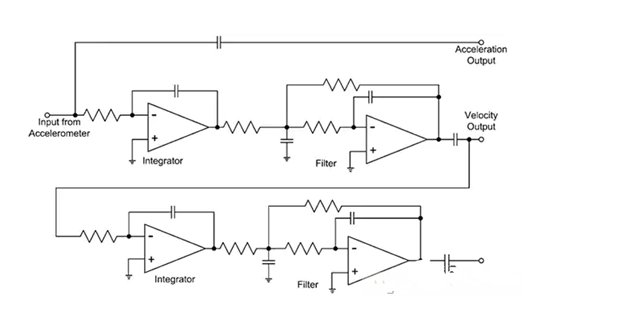
图 5：使用双积分器，设计人员可以从加速计产生加速度、速度和位移读数。

加速计的输入经过积分和滤波，得到速度。速度经过积分和滤波，可得到位移。请注意，所有输出均为交流耦合。这样一来，就不再需要处理每个积分器的初始条件。

四、函数发生器

函数发生器可输出多种波形，可以由多个积分器构成(图 6)。

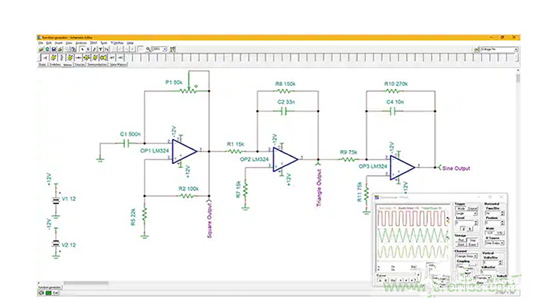
图 6：使用三个 LM324 级设计的函数发生器。OP1 是产生方波的张弛振荡器;OP2 是将方波转换为三角波的积分器;OP3 是另一个积分器，用作低通滤波器以消除三角波的谐波，从而产生正弦波。

函数发生器围绕 LM324 设计，而 LM324 是前面讨论的实用积分器。在该设计中，使用了三个 LM324 运算放大器，如 TINA-TI 仿真所示。第一级 OP1 用作张弛振荡器，并以 C1 和电位计 P1 确定的频率产生方波输出。连接的第二级 OP2 为积分器，将方波转换为三角波。连接的最后一级 OP3 为积分器，但用作低通滤波器。该滤波器去除三角波中的所有谐波，并输出基频正弦波。每级的输出显示在图 6 右下方的仿真器示波器中。

五、罗氏线圈

罗氏线圈是一类电流传感器，其利用缠绕在被测载流导体上的柔性线圈测量交流电源。它们用于测量高速电流瞬变、脉冲电流或 50/60 Hz 线路功率。

罗氏线圈执行的功能类似于电流互感器。主要区别在于罗氏线圈使用的是空芯，而不是电流互感器中使用的磁芯。空芯具有较低的插入阻抗，从而在测量大电流时响应更快且没有饱和效应。罗氏线圈非常易于使用(图 7)。

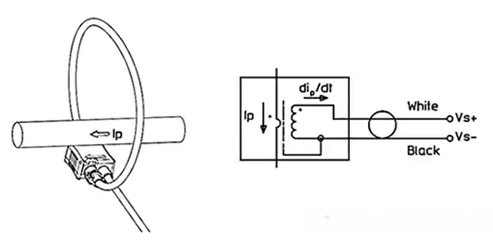
图 7：简化示意图显示了罗氏线圈在载流导体上的安装(左)和此设置的等效电路(右)。

罗氏线圈如 LEM USA 的 ART-B22-D300，简单地缠绕在载流导体上，如图 7 左侧所示。罗氏线圈的等效电路如右图所示。请注意，线圈的输出与被测电流的导数成正比。积分器可用于提取感测到的电流。

罗氏线圈积分器的参考设计如图 8 所示。此设计的特点是具有 0.5 至 200 A 范围的高精度输出(精度为 0.5%)，以及相同电流范围的快速建立输出(不到 15 ms 时间内的精度在 1% 以内)。

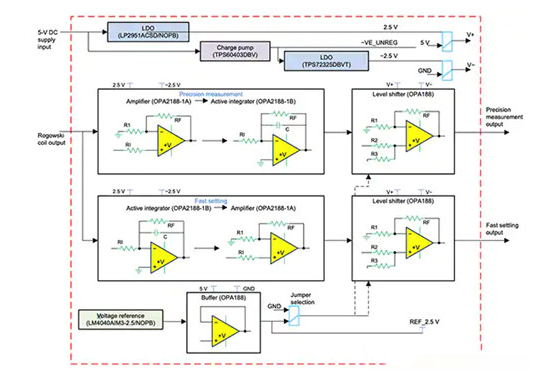
图 8：此罗氏线圈积分器的参考设计使用 Texas Instruments 的 OPA2188，作为设计积分器元件中的主运算放大器。

此参考设计使用 Texas Instruments 的 OPA2188，作为设计积分器元件中的主运算放大器。OPA2188 是一款双运算放大器，采用专有的自动调零技术，最大失调电压为 25 微伏 (µV)，并且时间或温度漂移接近于零。增益带宽积为 2 MHz，典型输入偏置电流为 ±160 pA。

对于该参考设计，Texas Instruments 选择 OPA2188 的原因是低失调和低失调漂移。而且，低偏置电流可最大程度地减小罗氏线圈上的负载。

六、滤波器中的积分器

积分器在状态变量和双二阶滤波器设计中都有使用。这些相关的滤波器类型使用双积分器来获得二阶滤波器响应。状态变量滤波器是一种更有趣的滤波器，因为单个设计会同时产生低通、高通和带通响应。该滤波器使用两个积分器以及一个加法器 / 减法器级，如 TINA-TI 仿真所示(图 9)。图中显示了低通输出的滤波器响应。

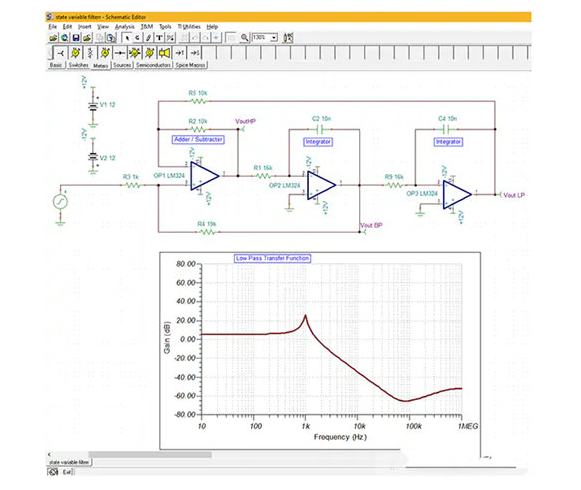
图 9：状态变量滤波器使用两个积分器和一个加法器 / 减法器级，以从同一电路产生低通、高通和带通输出。

这种滤波器拓扑的优势在于，在设计过程中可独立调节所有三个滤波器参数(增益、截止频率和 Q 值)。在此示例中，直流增益为 1.9 (5.6 dB)，截止频率为 1 kHz，Q 为 10。

高阶滤波器的设计通过串联多个状态变量滤波器来实现。这些滤波器通常用于模数转换器前的抗混叠，其中要求高动态范围和低噪声。

尽管有时候世界似乎已经全数字化，模拟积分器在信号处理、传感器调节、信号生成和滤波方面，仍然是非常有用和通用的电路元件。
编辑：hfy