基于FPGA的多级CIC滤波器原理

在实现多级CIC滤波器前我们先来了解滑动平均滤波器、微分器、积分器以及梳状滤波器原理。CIC滤波器在通信信号处理中有着重要的应用。

1、滑动平均滤波器

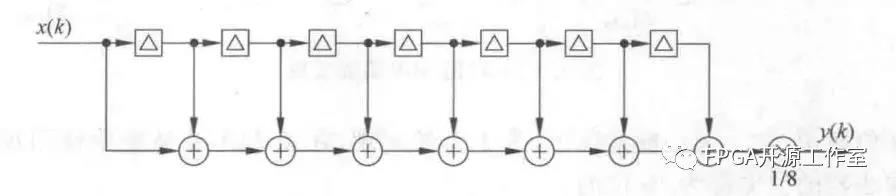
图1 8权值滑动平均滤波器结构

滑动平均滤波器(Moving Average Filter)的所有权值系数均为1，实现对信号的平滑作用，具有低通特性。

Matlab ：
close all
clear all
clc

%set system parameter
fs = 1000;    %The frequency of the local oscillator signal
Fs = 44100;   %sampling frequency
N =  24;         %Quantitative bits
L = 8192;

%Generating an input signal
t =0:1/Fs:(1/Fs)*(L-1);          %Generating the time series of sampling frequencies
sc =sin(2*pi*fs*t);        %a sinusoidal input signal that produces a random starting phase


%滑动平均滤波器
b =[1,1,1,1,1,1,1,1];
a =1;

sf=filter(b,a,sc).*(1/8);

 

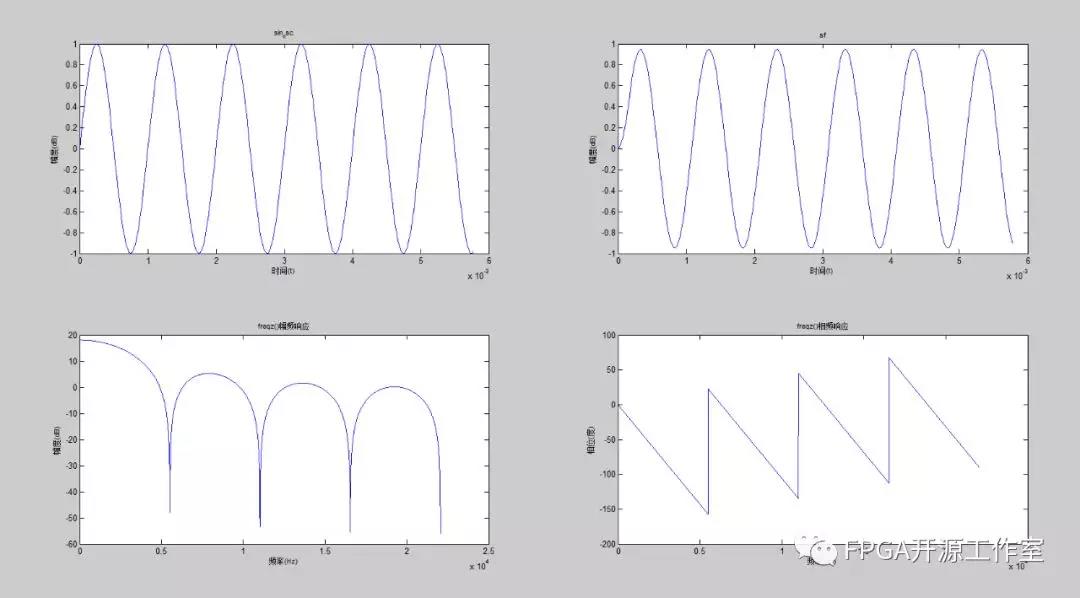
图2 滑动平均滤波器的幅频特征

2、微分器

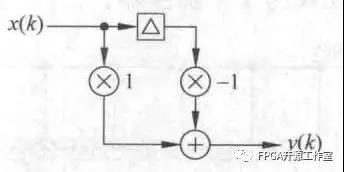
图3 微分器结构

微分器有1和-1两个权值系数的滤波器，该滤波器具有简单的高通幅频响应特性。

y( k ) = x( k ) - x( k - 1 )

Matlab :
close all
clear all
clc

%set system parameter
fs = 1000;    %The frequency of the local oscillator signal
Fs = 44100;   %sampling frequency
N =  24;         %Quantitative bits
L = 8192;

%Generating an input signal
t =0:1/Fs:(1/Fs)*(L-1);          %Generating the time series of sampling frequencies
sc =sin(2*pi*fs*t);        %a sinusoidal input signal that produces a random starting phase

%微分滤波器
b =[1,-1];
a =1;

sf=filter(b,a,sc);

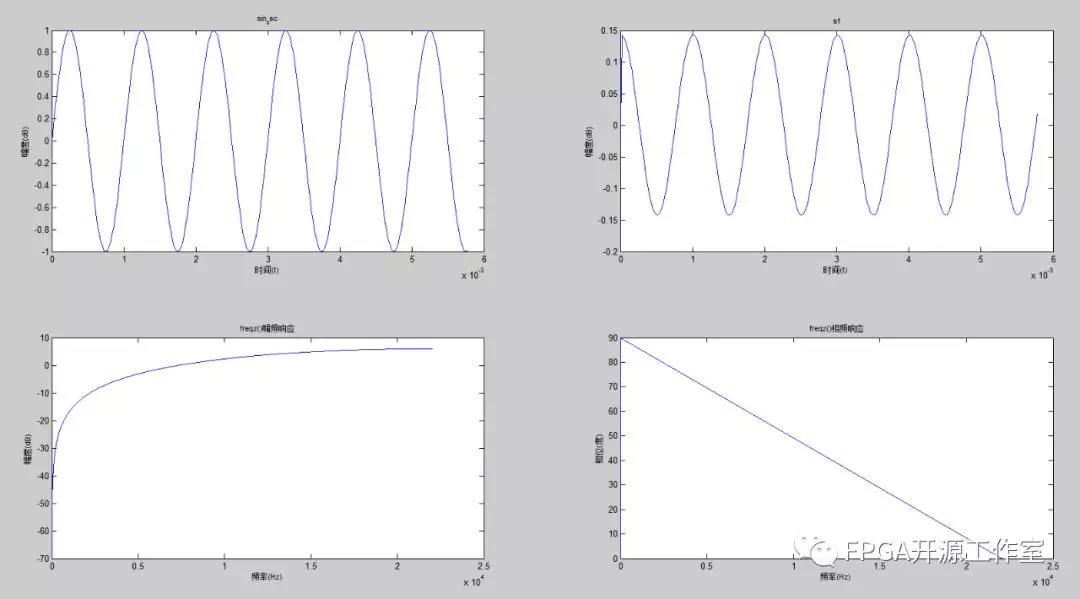
图4 微分器幅频响应特征

3、积分器

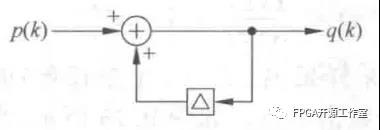
图5 数字积分器结构

数字积分器是只有一个系数的IIR滤波器该滤波器具有低通的滤波器的幅频响应特性。

q( k ) = p (k) + q( k - 1)

Matlab :
close all
clear all
clc

%set system parameter
fs = 1000;    %The frequency of the local oscillator signal
Fs = 44100;   %sampling frequency
N =  24;         %Quantitative bits
L = 8192;

%Generating an input signal
t =0:1/Fs:(1/Fs)*(L-1);          %Generating the time series of sampling frequencies
sc =sin(2*pi*fs*t);        %a sinusoidal input signal that produces a random starting phase

%积分滤波器
b =1;
a =[1,-1];

sf=filter(b,a,sc);

图6 积分器幅频响应特征

由图3，图4，和图5分析，1khz基本未发生改变，44.1khz相对于352.8khz采样率1khz点变得疏松。

编辑：hfy