

设计过程中如何使用节点分析的交流稳态值
描述
任何电路都可能难以手工分析,但是一些简单的技术可以帮助您在创建设计时准确地了解电压和电流在不同电路中的分布情况。欧姆定律,KVL和KCL是工程师和科学家学习用于电路设计和评估的基本方法,但是节点分析为设计人员提供了一种检查复杂电路中电压和电流分布的替代方法。无论选择哪种方式,您都可以获得相同的结果。
当查看具有时变源的交流系统时,您可能需要在节点分析中找到稳态值,尤其是当您知道系统中会有瞬态响应时。要在节点分析中获得稳态值,可以使用直流电路中相同的步骤。这是它在电路中的工作方式,以及在设计过程中如何使用节点分析的方法。
节点分析涉及以类似于基尔霍夫定律的方式确定电路中每个点的电压和电流。就像在KCL中一样,电路由多个节点组成,并且在系统中的每个节点处都计算出电压和电流。设置这些问题的过程非常简单,其目的是导出描述系统中电压和电流的线性方程组。
在电路中选择一个参考节点(通常作为接地)
使用KCL写出进入/退出每个节点的电流
写入相对于参考节点在每个节点上测得的电压
解决联立方程组以查找所有未知电压和电流
定义电压
步骤3非常关键,因为它根据节点和参考节点之间的电压差(即系统中最低的地电位点)来表示以KVL表示的电压降。但是,这使得节点分析比KVL更强大,因为它可以用于具有两种不同地电位的系统中。要查看系统中电压的定义方式,请看以下示例。在该电路中,有两个具有不同频率和2个阻抗的交流电压源。
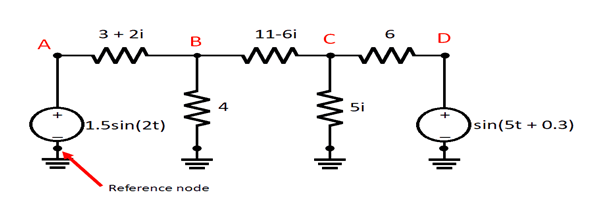
具有两个源的交流电路的节点分析。
请注意,在此电路中,我们已经指定了阻抗值。对于电容性或电感性阻抗,当系统由具有不同频率的源驱动时,您需要在频域而不是时域中考虑问题。在上述问题中,我们假设两个频率的复阻抗相同。在具有宽带移相器,衰减器或其他无源结构的RF系统中,这种情况将是典型的。
这个问题是在上述电路图中找到节点B和C处的电压和电流之一。请注意,由于所有电压测量均为差分测量,因此节点B和C处的电压是相对于左侧交流电源下方的参考节点定义的。假设参考节点定义为0 V,我们可以为节点B和C的电压构建以下方程式:
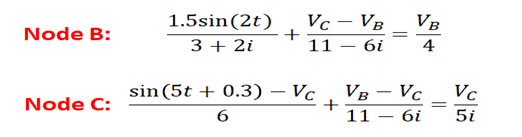
上例中显示的两个节点处的电压。
如果系统中有两个以上带有未知值的节点,我们可以对每个节点上的未知电压/电流应用相同的过程。现在的问题是在稳态下在上述等式中找到每个节点的电压之一。
在节点分析中找到稳态值
在上面显示的问题中,在以正弦波源驱动的系统中,每个节点处的稳态电压也将是周期波形。在这种情况下,如果两个源的频率不同,则产生的波形可能会非常复杂,但它们仍将是周期性的。要在节点分析中确定稳态值,只需对VB和VC求解上述方程式。通过以矩阵形式编写上述方程组,最容易做到这一点:
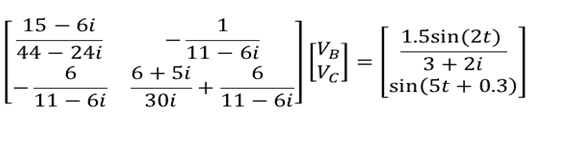
上例中显示的两个节点处的电压。
要求解此方程,只需将两边乘以系数矩阵的逆。现在,您将在节点B和C处获得电压。您会发现,在节点B和C处测得的结果波形是在节点A和D处测得的源电压的相当复杂的叠加。使用欧姆定律确定每个阻抗。
使用节点分析进行设计
通常,您在特定节点或一组节点之间具有电压/电流规格,并且需要找到产生该特定电流所需的正确阻抗值。上面的过程需要进行节点分析,然后反向进行。您知道电压和电流,但是您需要找到一个阻抗,该阻抗会产生相对于输入信号具有正确相位关系的正确电压/电流。
这是一个用节点分析,KVL或KVL解决的简单问题。他们都会产生相同的结果。这通常用于设计复杂电路,反馈环路和其他非重要电路中的分压器支路。您将拥有两个节点的已知电压,而不是未知的电压,但两个节点之间的阻抗将未知。现在,这成为使用为系统构造的方程式系统求解未知阻抗的问题。下面是上述电路的一个例子。
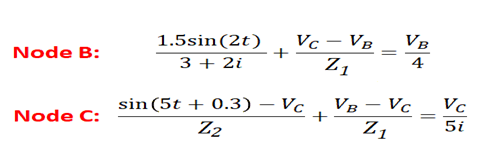
如果已知VB和VC,则可以通过求解上述方程组来确定Z1和Z2。
这样做的另一种方法是在电路模拟器中使用参数扫描。这涉及扫描电路元件的一系列值,并计算相关电路元件中的电压/电流。这在直流分析中特别有用,因为您将使用电阻器和电压/电流值。
编辑:hfy
-
使用AD2428时,通过主节点发现从节点的过程中遇到的问题求解2025-04-15 9568
-
刚接触LV还在自学过程中,想问问各位大神,属性节点怎么用?2016-10-30 3244
-
节点电压分析2020-10-05 3500
-
节点通信过程中遇到的问题2021-08-09 1977
-
数据校正在焦化碳一过程中的应用2009-02-10 661
-
正弦稳态电路的分析与计算2010-04-13 1021
-
高频PCB设计过程中的电源噪声的分析及对策2010-01-02 1339
-
微波器件薄膜化过程中的技术难点分析2012-06-01 1409
-
在线分析仪表在有色冶炼过程中的应用2017-02-07 854
-
FPGA系统复位过程中的亚稳态原理2020-06-26 1775
-
什么是稳态?浅谈稳态热分析的目的2021-01-14 10562
-
电源设计过程中器件和材料的测试和分析2020-12-15 734
-
正弦交流电路的稳态分析2021-06-19 1581
-
数据分析过程中几个可能常见的陷阱2021-09-23 2472
-
正弦交流电路的稳态分析相量法2023-10-28 3951
全部0条评论

快来发表一下你的评论吧 !

