深度学习中常用的几种卷积 不同情况下的卷积定义方式

在本文中，我尽量使用简单明了的方式向大家解释深度学习中常用的几种卷积，希望能够帮助你建立学习体系，并为你的研究提供参考。

Convolution VS Cross-correlation

卷积是一项在信号处理、视觉处理或者其他工程/科学领域中应用广泛的技术。在深度学习中，有一种模型架构，叫做Convolution Neural Network。深度学习中的卷积本质上就是信号处理中的Cross-correlation。当然，两者之间也存在细微的差别。

在信号/图像处理中，卷积定义如下：

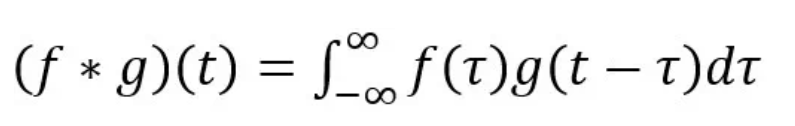
由上公式可以看出，卷积是通过两个函数f和g生成第三个函数的一种数学算子。对f与经过翻转和平移的g乘积进行积分。过程如下：

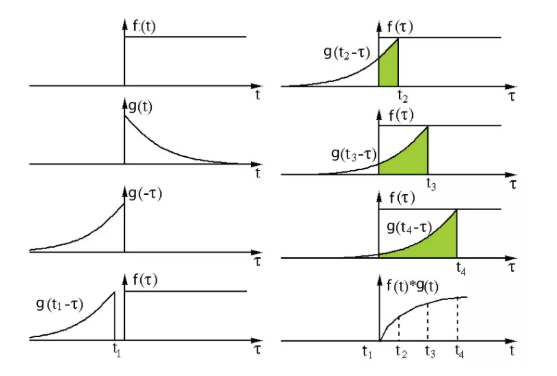
信号处理中的卷积。滤波器g首先翻转，然后沿着横坐标移动。计算两者相交的面积，就是卷积值。

另一方面，Cross-correlation被称为滑动点积或者两个函数的滑动内积。Cross-correlation中的滤波器函数是不用翻转的。它直接划过特征函数f。f和g相交的区域就是Cross-correlation。

在深度学习中，卷积中的滤波器不翻转。严格来说，它是Cross-correlation。我们基本上执行元素对元素的加法或者乘法。但是，在深度学习中，我们还是习惯叫做Convolution。滤波器的权重是在训练期间学习的。

Convolution in Deep Learning

卷积的目的是为了从输入中提取有用的特征。在图像处理中，有很多滤波器可以供我们选择。每一种滤波器帮助我们提取不同的特征。比如水平/垂直/对角线边缘等等。在CNN中，通过卷积提取不同的特征，滤波器的权重在训练期间自动学习。然后将所有提取到的特征“组合”以作出决定。

卷积的优势在于，权重共享和平移不变性。同时还考虑到了像素空间的关系，而这一点很有用，特别是在计算机视觉任务中，因为这些任务通常涉及识别具有空间关系的对象。（例如：狗的身体通常连接头部、四肢和尾部）。

The single channel version

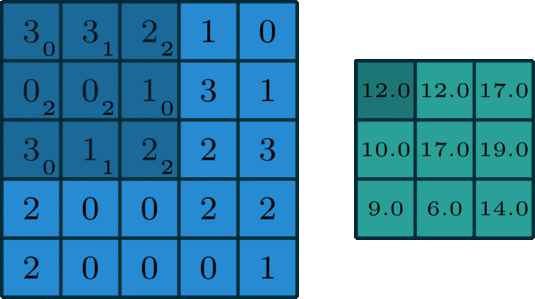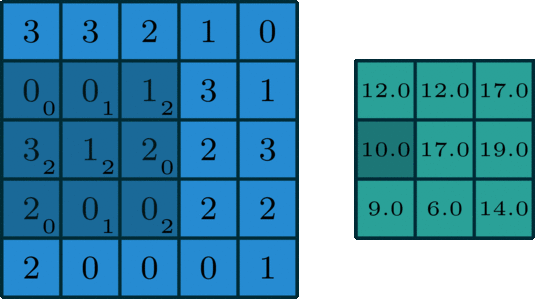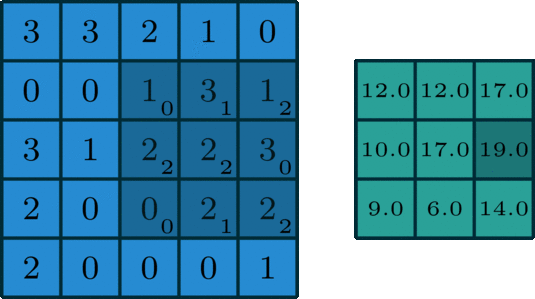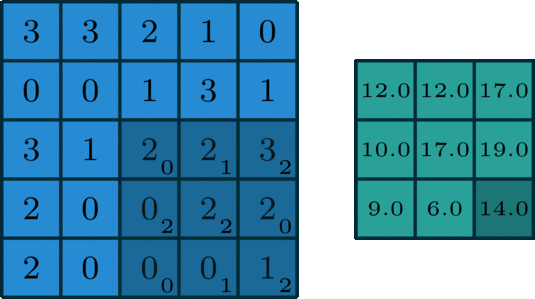
单个通道的卷积在深度学习中，卷积是元素对元素的加法和乘法。对于具有一个通道的图像，卷积如上图所示。在这里的滤波器是一个3x3的矩阵[[0,1,2],[2,2,0],[0,1,2]]。滤波器滑过输入，在每个位置完成一次卷积，每个滑动位置得到一个数字。最终输出仍然是一个3x3的矩阵。（注意，在上面的例子中，stride=1，padding=0）

The muti-channel version

在很多应用中，我们需要处理多通道图片。最典型的例子就是RGB图像。

不同的通道强调原始图像的不同方面另一个多通道数据的例子是CNN中的层。卷积网络层通常由多个通道组成（通常为数百个通道）。每个通道描述前一层的不同方面。我们如何在不同深度的层之间进行转换？如何将深度为n的层转换为深度为m下一层？

在描述这个过程之前，我们先介绍一些术语：layers（层）、channels（通道）、feature maps（特征图），filters（滤波器），kernels（卷积核）。从层次结构的角度来看，层和滤波器的概念处于同一水平，而通道和卷积核在下一级结构中。通道和特征图是同一个事情。一层可以有多个通道（或者说特征图）。如果输入的是一个RGB图像，那么就会有3个通道。“channel”通常被用来描述“layer”的结构。相似的，“kernel”是被用来描述“filter”的结构。

layer和channel之间，filter和kernel之间的不同filter和kernel之间的不同很微妙。很多时候，它们可以互换，所以这可能造成我们的混淆。那它们之间的不同在于哪里呢？一个“Kernel”更倾向于是2D的权重矩阵。而“filter”则是指多个Kernel堆叠的3D结构。如果是一个2D的filter，那么两者就是一样的。但是一个3Dfilter，在大多数深度学习的卷积中，它是包含kernel的。每个卷积核都是独一无二的，主要在于强调输入通道的不同方面。

讲了概念，下面我们继续讲解多通道卷积。将每个内核应用到前一层的输入通道上以生成一个输出通道。这是一个卷积核过程，我们为所有Kernel重复这样的过程以生成多个通道。然后把这些通道加在一起形成单个输出通道。下图：

输入是一个5x5x3的矩阵，有三个通道。filter是一个3x3x3的矩阵。首先，filter中的每个卷积核分别应用于输入层中的三个通道。执行三次卷积，产生3个3x3的通道。

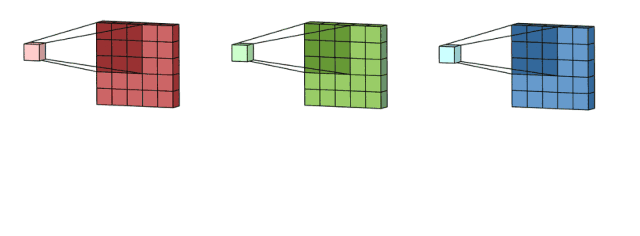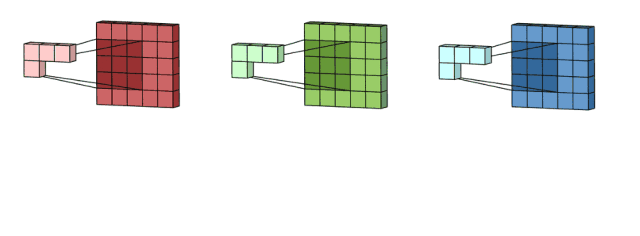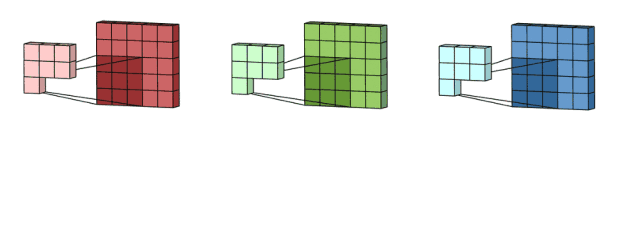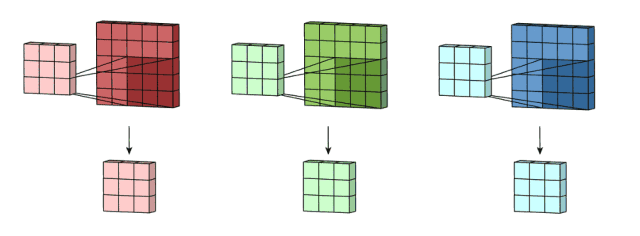
然后，这三个通道相加（矩阵加法），得到一个3x3x1的单通道。这个通道就是在输入层（5x5x3矩阵）应用filter（3x3x3矩阵）的结果。

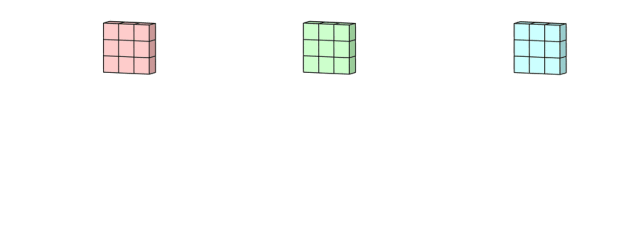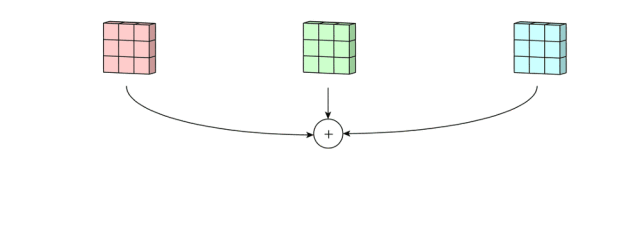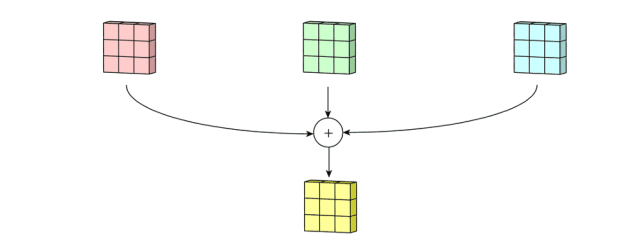
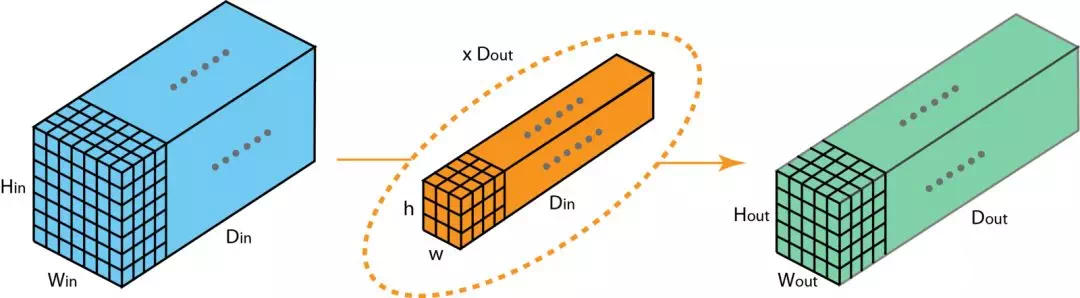
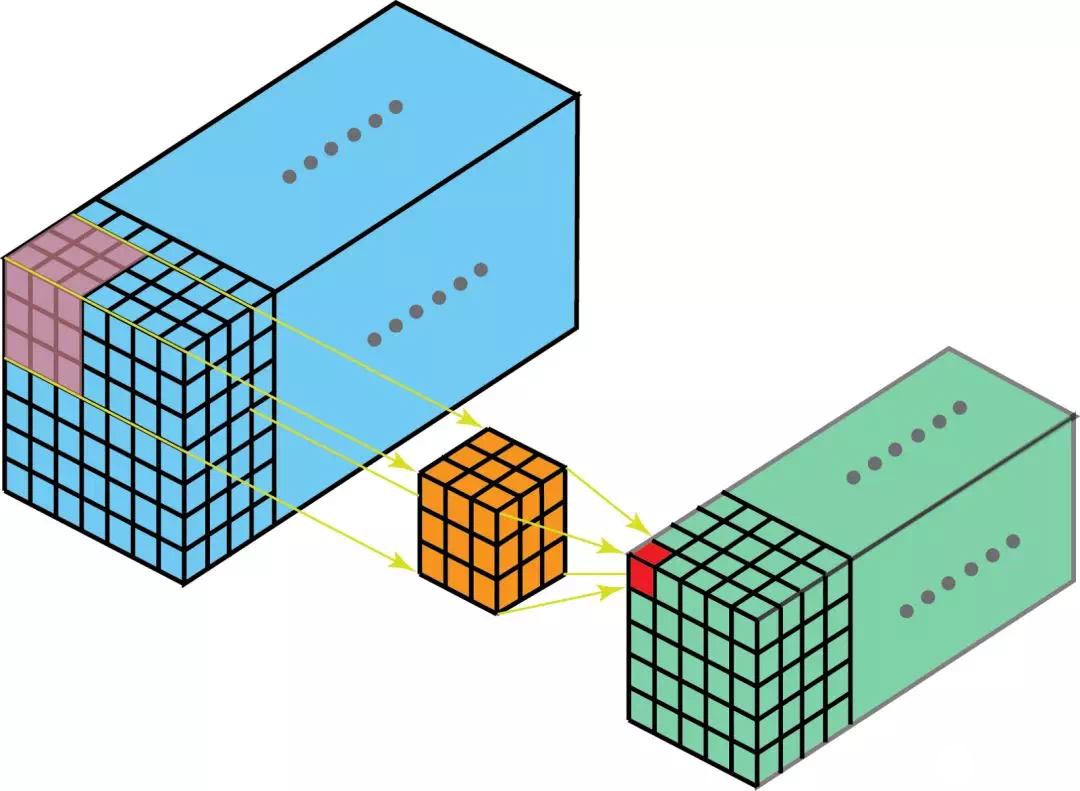
同样的，我们可以把这个过程看作是一个3Dfilter矩阵滑过输入层。值得注意的是，输入层和单个filter有相同的深度（通道数量=单个filter中卷积核数量）。3Dfilter只需要在2维方向上移动，图像的高和宽。这也是为什么这种操作被称为2D卷积，尽管是使用的3D滤波器来处理3D数据。在每一个滑动位置，我们执行卷积，得到一个数字。就像下面的例子中体现的，（正方形的那个侧面 记为输入图片长宽， 长方形的侧面，这个长 便反应出深度 = 即 对应的  通道数是多少 ）滑动水平的5个位置和垂直的5个位置进行。总之，我们得到了一个单一通道输出。

现在，我们一起来看看，如何在不同深度的层之间转换。假设输入层有xin个通道，我们想得到输出有Dout个通道。我们只需要将Dout 个 filters应用到输入层。每一个 filter有Din个卷积核。每个filter提供一个输出通道。完成该过程，将结果堆叠在一起形成输出层。

3D Convolution

在上一节的最后一个插图中，可以看出，这实际上是在完成3D卷积。但是在深度学习中，我们仍然把上述操作称为2D卷积。3D数据，2D卷积。滤波器的深度和输入层的深度是一样的。3D滤波器只在两个方向上移动（图像的高和宽），而输出也是一个2D的图像（仅有一个通道）。

3D卷积是存在的，它们是2D卷积的推广。在3D卷积中，滤波器的深度小于输入层的深度（也可以说卷积核尺寸小于通道尺寸）。所以，3D滤波器需要在数据的三个维度上移动（图像的长、宽、高）。在滤波器移动的每个位置，执行一次卷积，得到一个数字。当滤波器滑过整个3D空间，输出的结果也是一个3D的。

和2D卷积能够编码2D域中的对象关系一样，3D卷积也可以描述3D空间中的对象关系。3D关系在一些应用中是很重要的，比如3D分割/医学图像重构等。

1x1 Convolution

下面我们来看一种有趣的操作，1x1卷积。

我们会有疑问，这种卷积操作真的有用吗？看起来只是一个数字乘以输入层的每个数字？正确，也不正确。如果输入数据只有一个通道，那这种操作就是将每个元素乘上一个数字。

但是，如果输入数据是多通道的。那么下面的图可以说明，1 x 1卷积是如何工作的。输入的数据是尺寸是H x W x D，滤波器尺寸是1 x 1x D，输出通道尺寸是H x W x 1。如果我们执行N次1x1卷积，并将结果连接在一起，那可以得到一个H x W x N的输出。

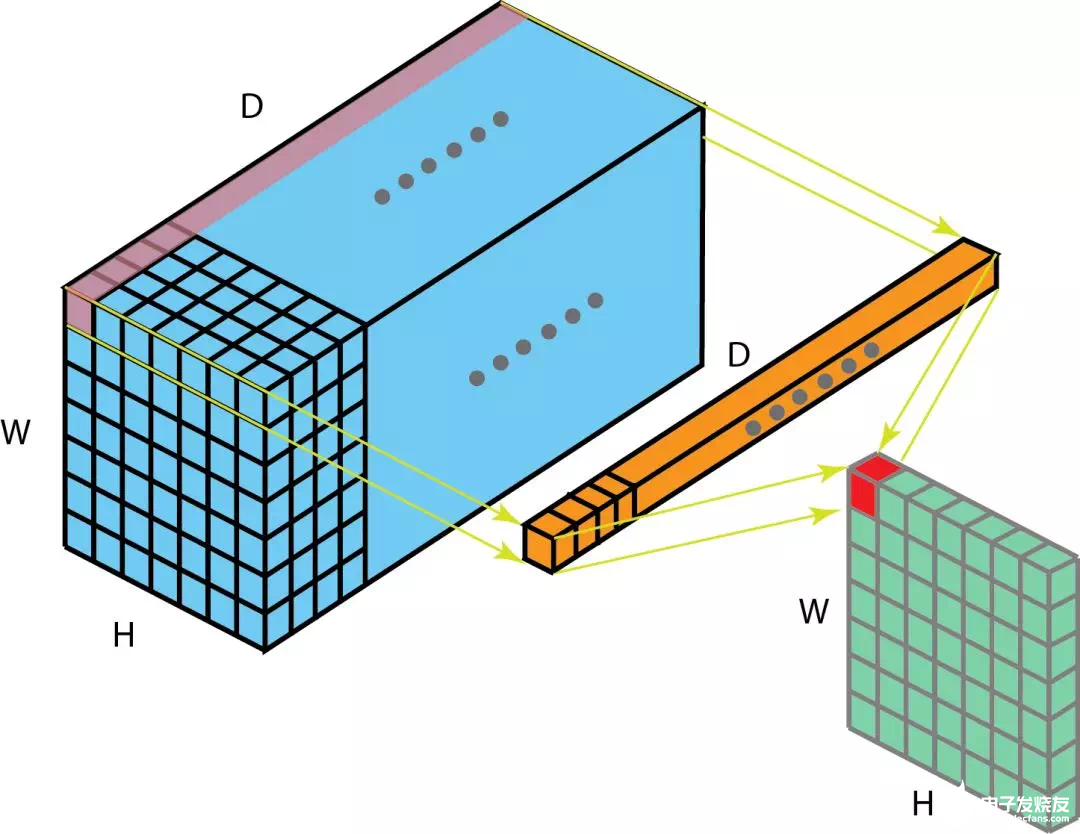
1 x 1卷积在论文《Network In Network》中提出来。并且在Google发表的《Going Deeper with  Convolution》中也有用到。1 x 1卷积的优势如下：

• 降低维度以实现高效计算
• 高效的低维嵌入，或特征池
• 卷积后再次应用非线性

前两个优势可以从上图中看出。完成1 x 1卷积操作后，显著的降低了depth-wise的维度。如果原始输入有200个通道，那么1 x 1卷积操作将这些通道嵌入到单一通道。第三个优势是指，在1 x 1卷积后，可以添加诸如ReLU等非线性激活。非线性允许网络学习更加复杂的函数。

Convolution Arithmetic

现在我们知道了depth维度的卷积。我们继续学习另外两个方向（height&width），同样重要的卷积算法。一些术语：

Kernel size（卷积核尺寸）：卷积核在上面的部分已有提到，卷积核大小定义了卷积的视图。

Stride（步长）：定义了卷积核在图像中移动的每一步的大小。比如Stride=1，那么卷积核就是按一个像素大小移动。Stride=2，那么卷积核在图像中就是按2个像素移动（即，会跳过一个像素）。我们可以用stride>=2，来对图像进行下采样。

Padding：可以将Padding理解为在图像外围补充一些像素点。padding可以保持空间输出维度等于输入图像，必要的话，可以在输入外围填充0。另一方面，unpadded卷积只对输入图像的像素执行卷积，没有填充0。输出的尺寸将小于输入。

下图是2D卷积，Kernel size=3，Stride=1，Padding=1：

这里有一篇写得很好的文章，推荐给大家。它讲述了更多的细节和举了很多例子来讲述不同的Kernel size、stride和padding的组合。这里我只是总结一般案例的结果。

输入图像大小是i，kernel size=k，padding=p，stride=s，那么卷积后的输出o计算如下：

编辑：hfy