为什么要可视化图 大规模图可视化攻略方案

　　如果你需要可视化一个大规模的图网络，而你尝试了各种各样的工具，却只画了一个小毛球就耗尽了你的 RAM，这时候你要怎么办？我的工作常常需要可视化大规模图（上亿的节点），尝试了非常多的工具和方法。但是，我却没有发现有人提供实用的攻略，于是，我决定根据自己的经验写一篇攻略。

　　为什么要可视化图

　　发现寻找的目标

　　通常，我们会将节点和边的集合作为输入，然后基于数据可以计算出一些统计信息，但是这不足以从结构中获得想法。好的可视化可以帮助我们清晰的发现图中的一些簇、 bridges 或者是点云，还有一些其他的模式。

　　便于解释

　　很明显，数据的可视化用于表示，这是一个展示工作成果的好方法。例如，如果你解决了一个聚类问题，你可以用不同的颜色表示不同的标签进行可视化，展示它们是如何连接的。

　　获得特征

　　尽管大多数图可视化工具都是为制作一些图片而创建的，但它们也很适合作为降维工具。以邻接矩阵表示的图是高维空间中的数据。绘制时，我们得到每个顶点的两个（通常）坐标。这些坐标也可以用作特征。这个空间中顶点之间的紧密性意味着相似性。

　　大规模图的问题

　　我将用大约 10K 节点和边的大图来表示。小规模的图，通过几分钟搜索到的工具基本上都可以解决。大规模图的难点在哪里呢？主要有两个问题：可读性和速度。通常，大规模图的可视化看起来会非常混乱，因为图中有太多对象。此外，图可视化算法的算法复杂度很高：边或者顶点数目的二阶或三阶依赖。即使只看一次结果，也要很久才能找到更好的参数。

　　已有的研究

　　Helen Gibson， Joe Faith and Paul Vickers： “A survey of two-dimensional graph layout techniques for information visualization”

　　本文介绍了有哪些图可视化方法存在，这些方法是如何工作的。文中将各种算法整理成了表，很清晰。我在这篇文章中也有用到了该文中的一些图表。

　　Oh-Hyun Kwon， Tarik Crnovrsanin and Kwan-Liu Ma “What Would a Graph Look Like in This Layout？ A Machine Learning Approach to Large Graph Visualization”

　　这篇文章的工程量很大。研究人员尝试了所有可能的算法，然后可视化出来，手工评估相似度。之后，他们拟合模型来预测图在 layout 中是什么样子。我也用了一些这篇文章的图片。

　　理论部分

　　Layout 是一种将坐标映射到每个节点的方法。通常，这是指 2D 平面上的坐标。

　　什么是好的 Layout

　　很容易评价一个东西看起来是好还是坏，但是很难制定机器评估好坏的标准。为了得到所谓的“好的” layout，可以使用以下这些指标：

　　1. Minimum edges intersection（最小边交）

　　很容易理解，太多的交叉会让图看起来很凌乱。

　　2. 相邻的节点彼此靠近

　　逻辑相连的顶点应该彼此靠近，通过定义，它们代表了图中存在的主要信息。

　　3. 社区聚类

　　如果一些节点之间的连接比与其他节点之间的连接频率更高，那么它们看起来像密集的云。

　　4. 最小的重叠边和节点

　　这也是很明显的，如果我们不能确定是一个或者几个节点，那么该图可视化的可读性就很差了。

　　Layout 的类别

　　

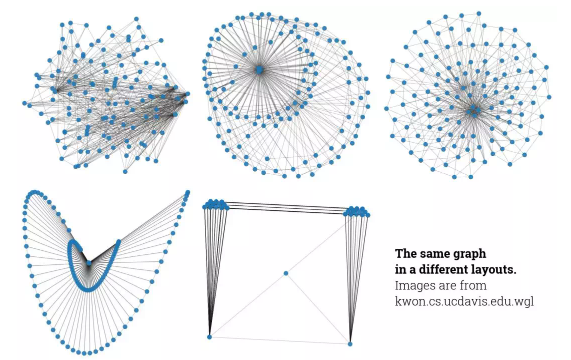
　　同一个图在不同 layout 上的呈现。

　　我考虑着重介绍三种比较重要的 Layout，layout 的分类方法有很多，下面这种分类足以涵盖所有可能的类型。

　　力导向和基于能量

　　降维

　　基于节点特征

　　力导向

　　

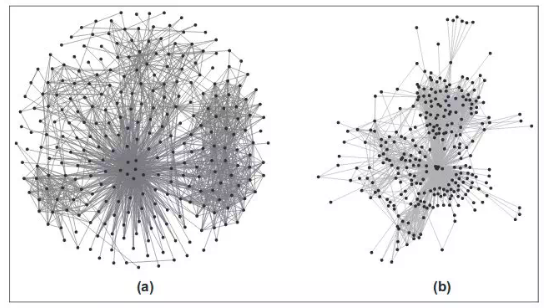
　　这一类方法是基于物理系统仿真的。顶点表示为相互排斥的带电粒子，边被视为弹性线。这些方法试图建立这个系统的动力学模型或找到最小能量。这些图通常会比较好的反应图的拓扑结构，但是计算非常复杂，需要调节非常多参数。

　　该方法的重要成员包括 Force Atlas，Fruchterman-Reingold，Kamada Kawaii and OpenOrd。最后一种会使用一些优化方法来减少计算量，比如削减长边，但是作为副作用，会让图更加聚集。

　　降维

　　

　　一个图可以用一个 N x N 的邻接矩阵来表示，N 代表节点的数量。该矩阵同样可以看作是 N 维空间中的 N 个对象。这种表示允许我们使用通用的降维方法，比如 PCA、UMAP、tSNE 等等。另一种途径就是计算节点之间的理论距离，并在低维空间中保持该比例。

　　基于特征

　　

　　通常，图数据都和现实生活中的对象相关联。因此，顶点和边会有自己的特征。因此我们可以用这些特征来表示它们。我们可以利用上面讲到的降维方法，像处理表数据一样处理节点的特征，或者直接绘制节点特征对的散点图。值得一提的是 Hive Plot，因为它和其他的方法都不同。在 Hive Plot 中，节点与多个径向轴对齐，边是它们之间的曲线。

　　大规模图可视化工具

　　虽然图可视化是一个老生常谈的问题，但是支持大规模图可视化的工具仍然捉襟见肘。其中有很多都被它们的开发者遗弃了。并且其中有很多都有自己明显的缺陷。我只介绍这些工具中值得被提及并且支持大规模图的，这样可以帮助大家快速寻找到一个靠谱的工具，并且它还工作的很好。

　　GraphViz

　　

　　2011年以前的比特币交易图

　　

　　有些时候，调参非常困难

　　这是一款 old-school CLI 工具，它有自己的图定义语言，叫做“dot”。这是一个有几个 layouts 的包。针对大规模图，它有 sfdp layout，来自于力导向家族。该工具的优点和缺点一样：它从命令行运行。它对自动化很有用，但是没有互动性的调参非常困难。你根本不知道你自己会等多久才能得到最后的结果，也不知道是否是需要停止它，并使用其他的参数重新开始。

　　graphviz.org

　　Gephi

　　

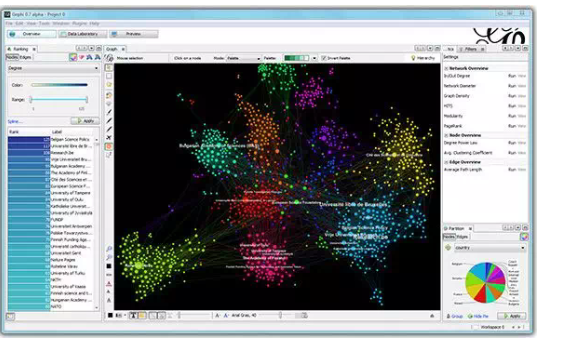
　　Gephi 图界面

　　来自 iMDB 的 13K 的电影推荐系统的图

　　这是我知道的最好的图可视化工具。它有 GUI，包含一些 layouts 和很多图分析工具。还有很多社区贡献的插件。例如我最喜欢的 layout，“Multigravity Force-Atlas 2” 或者 sigma.js 传播工具，并且提供交互式的网页端页面。在 Gephi 中，可以根据节点和边的特征设置颜色。

　　但是 Gephi 仍然被开发者抛弃了。它还有一点老式的 GUI 和一些简单的特征。

　　gephi.org

　　igraph

　　

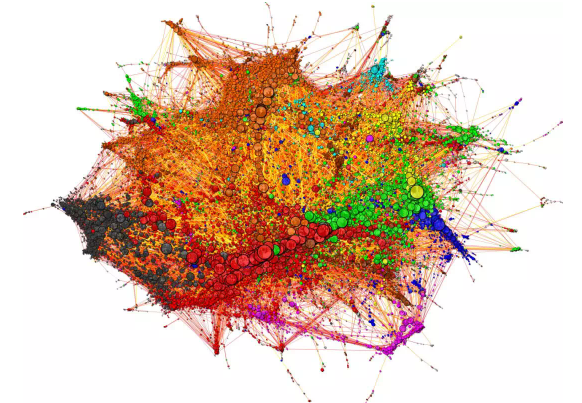
　　音乐推荐图

　　我需要向这个通用图分析的工具致敬。其中最令人印象深刻的图可视化是由 igraph 的一位作者制作的。igraph 的缺点对于 python API 来说是糟糕的文档，但是源代码是可读的并且注释良好。

　　igraph.org

　　LargeViz

　　

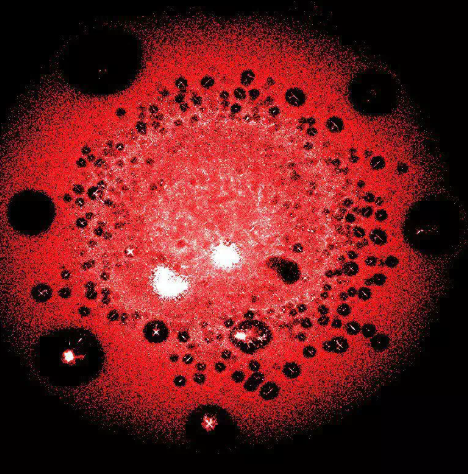
　　最大的比特币集群，里面有几千万个节点（交易和地址）

　　当你需要绘制一个巨大的图时，它将是伟大的救世主。LargeViz 是一种降维工具，不仅可以用于图，还可以用于任意表数据。它从命令行运行，工作速度快，占用较少的内存。

　　arxiv.org/abs/1602.00370

　　github.com/lferry007/LargeVis

　　Graphistry

　　

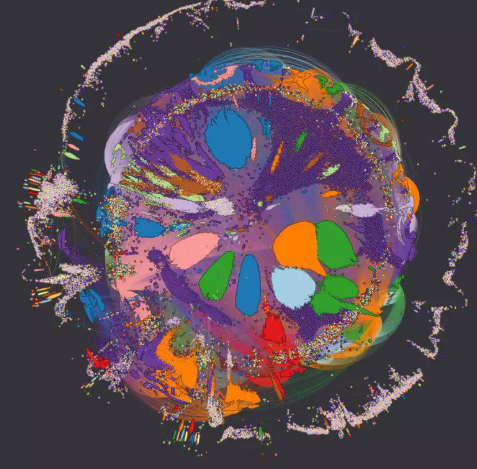
　　一周内可能被黑客攻击的地址以及交易

　　

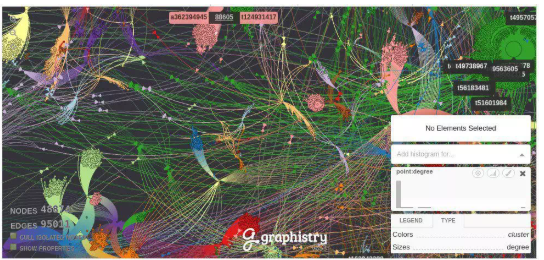
　　直观并且美观的界面，但是很有限

　　该工具是这篇攻略中唯一需要付费的。Graphistry 是一种服务，直接输入数据，并进行所有计算，只需要在客户端浏览器查看漂亮的图片。Graphistry 出了具有合理的默认参数，良好的配色方案和稍好的交互性之外，其他特性与Gephi 相比并没有太大的改进。它只提供一个力定向 layout 并且还具有800K个节点或边的限制。

　　www.graphistry.com

　　Graph Embeddings

　　也有一种方法可以解决疯狂的尺寸问题。从大约一百万个顶点开始，只需要合理地查看顶点密度，而不需要绘制边和特定的顶点。因为没有人能在这样的图上辨认出单个的物体。此外，大多数用于图可视化的算法将在这样的大小上工作很多小时，甚至几天。如果我们稍微改变一下方法，这个问题就可以解决。有很多方法可以得到反映图顶点特征的固定大小表示。在得到这样的表示之后，你唯一需要做的就是把维数降到2，以便得到一张图片。

　　Node2Vec

　　

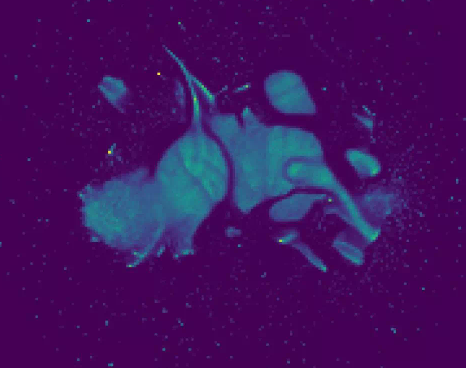
　　Node2Vec + UMAP

　　这是 word2vec 在图的改编。图中使用随机游动而不是单词序列。因此，该方法仅使用有关节点邻域的信息。在大多数情况下，这就足够了。

　　snap.stanford.edu/node2vec

　　github.com/xgfs/node2vec-c

　　VERSE

　　

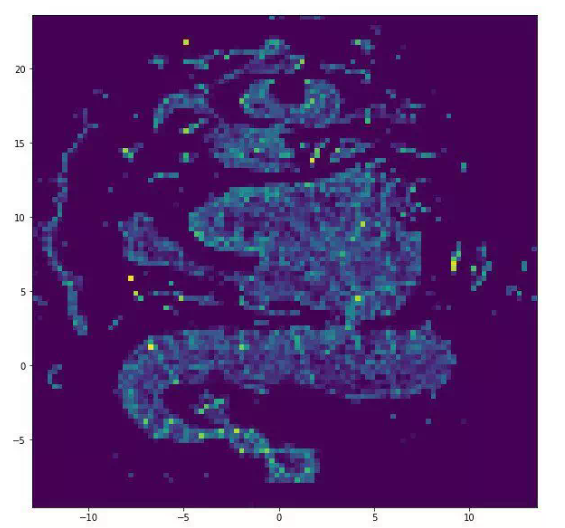
　　VERSE + UMAP

　　用于通用图表示的高级算法，是我用起来最好的之一。

　　tsitsul.in/publications/verse

　　github.com/xgfs/verse

　　Graph Convolutions

　　

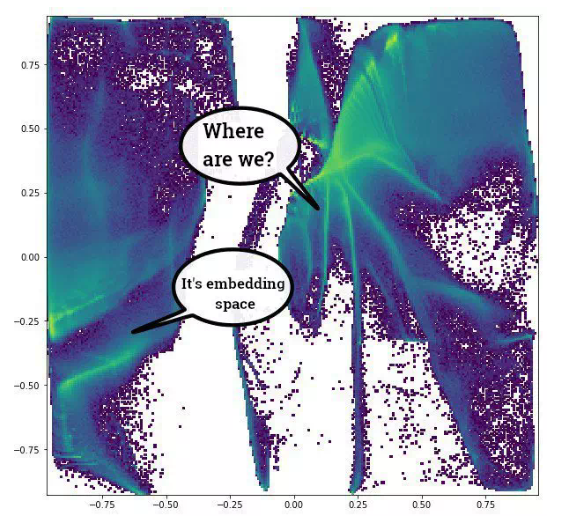
　　图卷积+ 自编码器 二部图

　　有很多方法可以定义图上的卷积。但事实上，这是顶点邻居的简单特征“扩散”。我们还可以将局部拓扑信息放在顶点特征中。
编辑：hfy