DAC和ADC响应发生意外滚降的情况解决方案

你在绘制某个信号处理系统的频率响应时，是否遇到过意外滚降的情况——原本预计它是平坦的（或至少跟所设计的曲线差不多），但结果却平稳而慢吞吞地滚离了目标值，而让你大失所望？如果你遇到过这种情况，那你就受到了sinc（）频率响应的影响。下面来看看具体情况。

这个滚降问题可能会在采样数据系统的输入和输出中出现。先来看一下输出。如果你想要将一串样本值转换回模拟信号，那么可以将这些数字样本送到DAC。现在，大多数DAC IC和模块都具有“保持”输出。也就是说，当它们接收到一个新的数字样本时，输出电压会迅速变为相应的新值并保持在那里，直到出现下一个样本。这种现象非常普遍，以至于许多工程师会认为这是正常现象，并认为此类DAC的输出电压以某种方式正确地代表了样本流（除了有一些令人讨厌的高频噪声外）。

事实并非如此。这种“保持”过程会使这种系统的频率响应与仅在每个采样时刻非常短暂地确定输出电压的系统不同。这种尖峰输出电压在实际应用中很不方便，这就是为什么我们很少遇到它。

将每个样本的电压扩展至“填充可用的空间”，是零阶保持器的一个示例。这种系统的输出频谱等于理想的尖峰输出系统的频谱乘以两个采样点之间矩形脉冲的频谱，也即其宽度与采样间隔相等。这样的矩形时间响应与具有sinc（）特性的频率响应对应。sinc（x）是sin（x）/x的缩写，而一个域中的矩形与另一个域中的sinc（）之间存在傅立叶镜像对应，这不仅在信号理论而且在整个物理学都非常常见。

计算sinc函数的值——参数x的值是π乘以信号频率（f）与采样频率（fs）之比，即sinc（πf/fs）——可知在大约fs的0.444倍处，滚降已经达到-3dB。图1给出了在每秒1个样本（sps）的采样速率下sinc（）滚降的频率效应。请注意，它在采样率倍数的频率处具有深而窄的陷波。

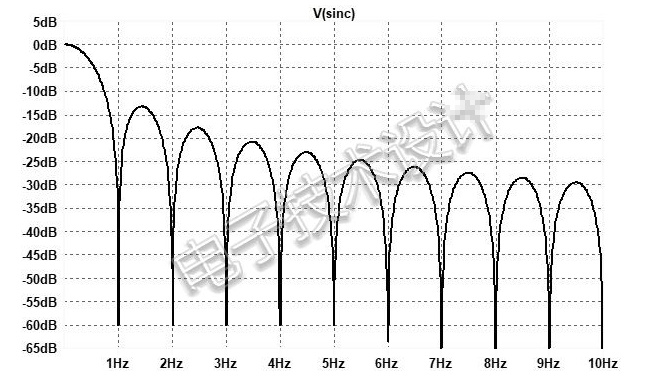
图1：每秒1个样本的零阶保持器的sinc（）响应，从中可以看到在采样频率倍数处具有深陷波。

现在来看时域当中的情况。图2显示了一个0.444Hz正弦波以及每秒对其采样一次的结果。样本所达到的峰值显然是输入电压的峰值。但是，随着采样时钟在信号上“走动”，某些区域的低输出电压会持续一段相当长的时间。

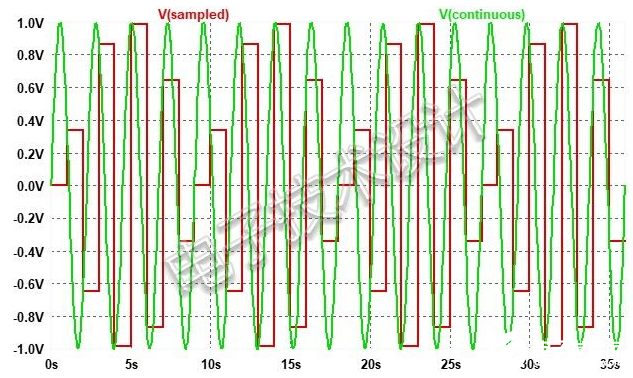
图2：以每秒1个样本的速度采样并保持的0.444Hz正弦波，从中可看到具有衰减峰值的长段。

0.444Hz信号仍然存在，但由于某些能量已移至较高频率的“图像”中，因此其水平已经降低了，如图3所示。可以看到输入信号的单个傅立叶分量会比输出信号中0.444Hz分量的值高3dB。

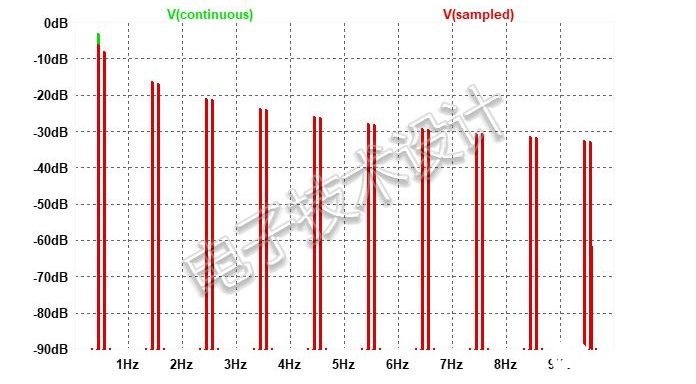
图3：以每秒1个样本的速率采样并保持的0.444Hz正弦波的频谱图，表明原始信号中的某些能量如何分布在多个图像上。

得出的结论是，采样正弦波的峰峰值不是衡量基频所含能量的好方法。相反，随着输入频率的增加，输出信号中的能量会越来越多地逐渐驻留在这些较高频图像分量上——这些分量是我们通常试图滤除的污物，以便获得良好的干净输出信号。因此就出现了滚降。

请注意，专为音频市场设计的现代DAC不会出现这个问题。这是因为它们每个样本不只更新一次，然后保持信号。它们在转换器的内部深处运行得更快，然后运用数字滤波技术来产生输出，这样在偶然检查中就完全看不到被采样的现象。获得具有超平坦频率响应的音频DAC非常容易，这也让工程师容易忘记“老式”采样DAC不具有这种平坦响应特性。

这就是我们系统输出部分的“原因”。当我们在数字域中分析数据而没有回到模拟状态时，输入通路是否还会导致可能检测到的滚降？好吧，是的，有时候可以。让我们看看这种情况。

如果使用的是采样ADC，那么答案通常是“不用担心”。这种ADC会在短暂的时间“缝隙”内拍摄输入信号的快照。通常，这个缝隙比两次采样之间的时间要窄得多，因此它对频率响应的影响不明显。但是，如果使用的是针对工业仪器仪表应用的Δ-Σ ADC，则滚降的幅度可能会超出预期。

Δ-Σ ADC具有滚降频率响应的原因在于，它们用来平滑其前端“调制器”中快速脉冲流的均值滤波器，具有与上述零阶保持器类似的脉冲响应。实际上，在任何给定的频率下，响应的滚降通常会恶化2至4倍。这是因为所使用的滤波器通常至少实际上是两到四个均值滤波器的级联。

例如，对于我在高性能应用中使用多年的赛普拉斯PSoC3和PSoC5器件中的Δ-Σ ADC来说，该ADC的抽取滤波器具有四个级（在其大部分范围内），因此具有sinc4（）响应。因此，在任何给定信号频率下，它的滚降幅度都是图1所示的四倍（以dB表示）。换句话说，它在0.443倍fs时为-12dB。当你真正想要的只是简单的称重时，这样大的频率响应平坦度偏差就无关紧要。但是对于大多数音频、通信和振动测量系统来说，这就非常可怕了。这个偏差在你把数字信号送到DAC，产生额外的滚降信号之前就已有之。

不过，这种响应效应也有好的一面。图1表明，sinc（）响应在fs的约1.43倍处“反弹”至约13.3dB。这提醒我们，简单的平均器对于消除高频变化来说并不是很好的滤波器。但是，如果将四个平均器串联起来获得sinc4（），则得到的阻带响应仅会反弹至53dB左右，如图4所示。这是非常有用的滤波，通常对于在没有太多高频干扰的时域中进行精确测量已经足够了。

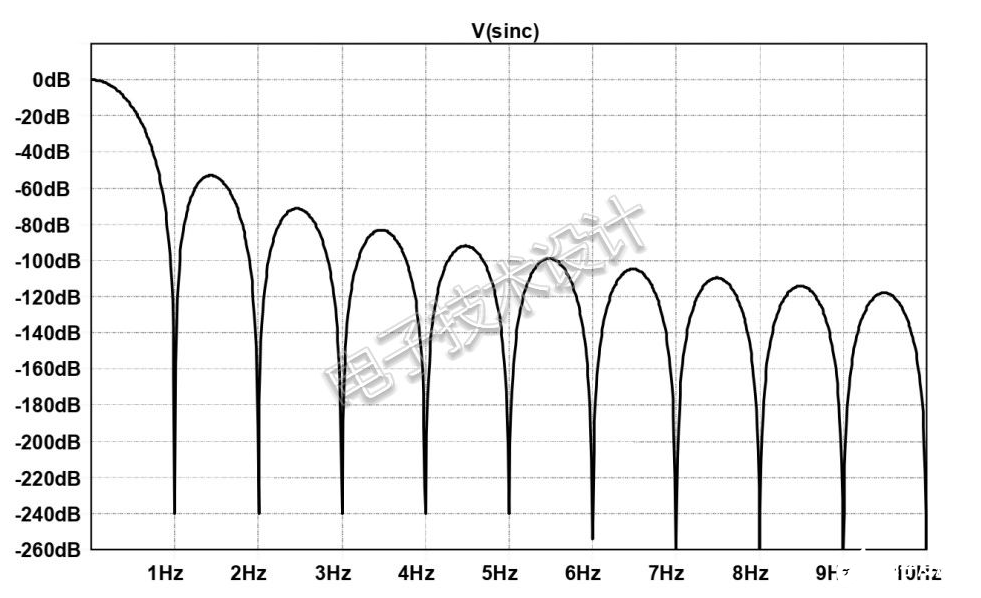
图4：PSoC3 ADC抽取滤波器的sinc4（）响应的“反弹”比简单的平均器要低得多。

因此，当需要平坦的频率响应而又确实必须使用保持DAC、Δ-Σ仪表ADC或同时使用两者时，该怎么办？现在你应该能够预料，推荐的解决方案涉及一个滤波器，结果不会让你失望的！
编辑：hfy