

PCB设计中简单谐波运动是如何产生的
描述
回到基本的力学或物理课程,有一个特定的示例总是用来引入振荡:谐波运动。这种基本的周期性运动描述了最基本的振荡类型,其中系统以正弦轨迹运动。尽管这是许多其他现象的数学基础的基本主题,但电路和机械中的实际振荡并不总是遵循纯谐波运动。取而代之的是,振荡可能是由复杂的频率混合引起的,从而导致周期性行为,而不仅仅是正弦波。
PCB设计中当您分析具有非线性成分的复杂电路时,即使系统由纯谐波源驱动,您也可能会注意到一系列复杂的振荡行为。是什么原因导致这种行为,以及它如何影响电气行为?如果您的系统中具有非线性组件,则需要使用一些基本模拟来了解不同的频率将如何引起与谐波运动甚至混沌振荡的偏差。阅读更多内容以了解这些非谐波振荡会在何处发生以及如何在不同类型的系统中产生。
为了更好地理解为什么系统可能表现出不稳定的行为,我们需要简要回顾一下简单的谐波运动是如何产生的。一旦我们看到了非线性在这些系统中发生的位置,就变得更加清楚如何无法通过插入正弦解简单地解决非线性系统。
首先,我们有一个线性振荡器的基本公式,如下所示。量u(t)可以是系统中的机械运动,电压,电流或其他一些相关量。f(t)项是强迫函数,可以是时间的任何连续或分段函数。对于电气系统,这是您用来描述RLC电路或以线性方式运行的非线性电路中的振荡的方程式。
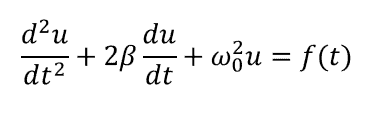
线性电路中的电压,电流或功率受时间相关的强制功能驱动。
当f(t)=
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
使用PCB设计运动感应灯2022-07-11 623
-
【PCB设计】PCB设计中的过孔分析2022-10-25 8263
-
PCB设计流程与PCB设计检查表介绍2023-03-08 5241
-
热门PCB设计技术方案2014-12-16 14388
-
如何减少PCB设计中的谐波失真?2021-04-21 1439
-
PCB设计中有效减少谐波失真的方法2021-04-23 1329
-
PCB设计时的谐波失真是如何产生的?2021-12-30 23887
-
PCB设计中的过孔问题讨论2009-11-11 1524
-
减少谐波失真的PCB设计方法2010-05-05 1380
-
PCB设计相关经验分享及PCB新手在PCB设计中应该注意的问题2013-09-06 1332
-
PCB设计中ESD防护的优化原则和技巧2019-04-16 1819
-
EAGLE CAD怎样做更简单的PCB设计2019-09-10 10014
-
简单三步教你进行PCB设计隐患分析2022-03-07 3063
-
PCB设计中基板产生的问题及解决方法2023-11-15 918
-
谐波怎么处理最简单的方法2025-07-13 2146
全部0条评论

快来发表一下你的评论吧 !

