

米勒效应使电压放大器的输入和输出实例分析
描述
作者:Stephen Woodward
虽然最初人们认为米勒效应只不过是会限制带宽和稳定性的不想要的寄生电容倍增器,但它现在已被有用的拓扑所采纳,如模拟示波器时基积分器。根据这样一个事实:如果放大器增益(A)可变,那么米勒阻抗(Zm)或电纳(Ym)也变,本设计实例提出了另一种使用它的好办法。一个世纪前提出的米勒效应使电压放大器的输入和输出之间连接的阻反映在抗放大器输入阻抗中,与放大器增益成比例缩放。虽然最初人们认为它只不过是会限制带宽和稳定性的不想要的寄生电容倍增器,但米勒效应已被有用的拓扑结构所采纳,如模拟示波器时基积分器。
根据这样一个事实:如果放大器增益(A)可变,那么米勒阻抗(Zm)或电纳(Ym)也可变,本设计实例提出了另一种使用它的好办法。
Zm = Z/(1–A)
Ym = Y(1 – A)
我们可以看到一个有趣的结果,使增益因子A包括A=+1,因此(1-A)=(1-1)=0,这导致了Zm(即Lm或Rm)理论上可至无穷大,而Ym(Cm)为零。
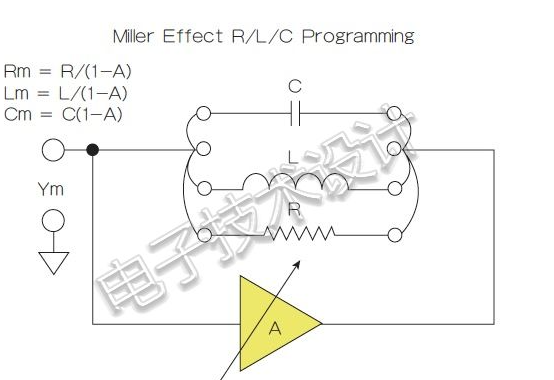
图1:反馈阻抗的可变增益米勒效应缩放。
图2中提出了米勒效应元件合成电路的一种实现方法。
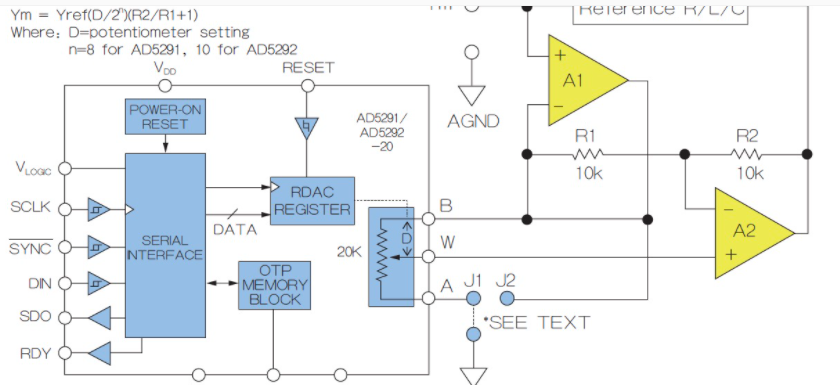
图2:可变增益米勒电路示例。
增益设定电位器(如简单的模拟微调器、带计数转盘的精密电位器或图示的数字电位器)的选择是根据应用需求而定的。A1和A2的选择需适应所需的带宽、电压规格和电流驱动能力,而R2/R1比率确定增益调节范围:(+1至-R2/R1)。以图2给定的元件为例(10位分辨率AD5292-20数字电位器),R1=R2,Yref=0.5µF参考电容,跳线J1接地,Ym可以以大约1nF(实际为977pF)每步、总共1k步,从大约为0(几个pF)合成到1.0µF:
Cm = 0.5µF(D/1024)(2)
0 ≤ D ≤ 1023
由此产生的电路可用于原型设计、测试、后期微调、调整和校准。
但是,这里存在一个明显的局限。合成电抗只有一个有源端子,另一端间接接地。这在许多潜在的应用中都存在问题。当需要两个端子时,也存在一种解决方案,如图3所示。
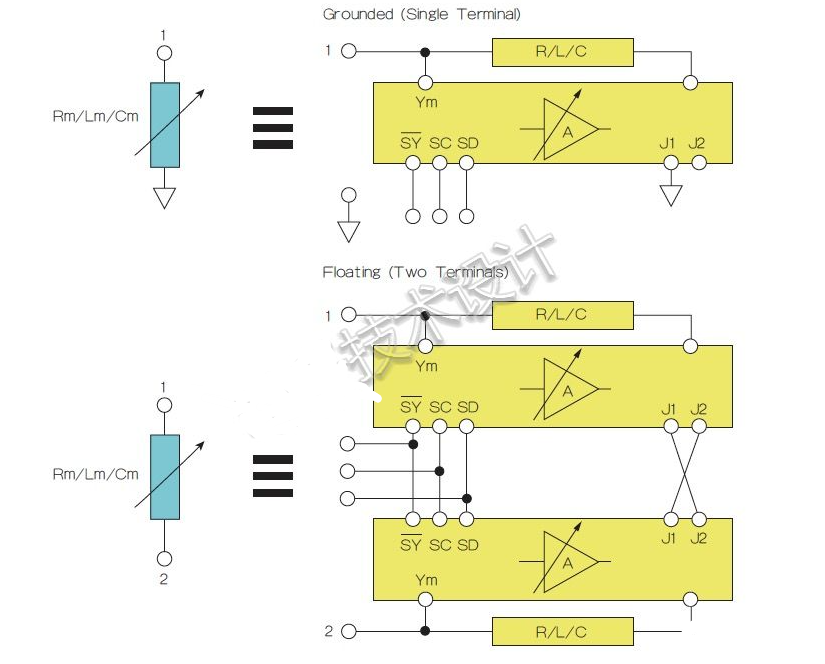
图3:单端子和双端子拓扑图。
这种解决方案是将两个相同的米勒电路(包含相同的参考电抗和电位器设定值)连到两个端子,并通过J1/J2交叉连接,然后利用合成电抗上出现的差分信号。两个电路中的米勒增益放大器减去出现在对端的信号,从而在两个端子间有效合成一个浮置元件。
编辑:hfy
-
电压放大器介绍,Agitek300Vp-p电压放大器2017-09-18 3077
-
电压放大器如何选择型号规格(电压放大器选型标准)2022-11-18 2023
-
电压放大器和电荷放大器本质上有何不同2023-05-30 1898
-
电压放大器结构组成 电压放大器的原理2023-06-01 3897
-
电压放大器的空载是指什么2023-07-24 3073
-
电压放大器工作在什么状态2023-08-02 1500
-
安泰电压放大器怎么用2024-02-29 1078
-
安泰电压放大器的选型标准有哪些2024-08-26 810
-
安泰电压放大器对参数的要求有哪些2024-09-12 809
-
Aigtek:电压放大器的输出特性有哪些2024-09-26 1040
-
Aigtek:电压放大器应用原理介绍2024-12-12 916
-
安泰:电压放大器原理和作用是什么意思2025-01-02 850
-
电压放大器为什么能放大功率2025-01-10 1067
-
电压放大器的设计过程及原理是什么2025-01-14 1234
-
Aigtek:电压放大器如何选择2025-02-12 889
全部0条评论

快来发表一下你的评论吧 !

