浅谈电路设计中运用叠加定理的独立源电路

本文主要运用叠加定理来介绍电路设计中的独立来源。

线性电路具有超校准能力

在电路设计中，叠加定理非常重要，也是我的最擅长的。该定理显示为：

“线性双边网络中任何电路元件中的电流或跨任何元件的电压是每种能源分别产生的电流或电压的代数和。”

从最基本的意义上讲，叠加定理告诉我们如何求解具有多个独立源的电路。使用这种方法，我们可以一一考虑源的影响。具有n个独立源的电路需要求解n个独立的电路。

尽管对于在求解复杂网络时避免联立方程，叠加定理似乎是正确的，但它仅适用于线性电路和线性电路响应。当我们想到欧姆定律时，我们正在使用线性组件，例如电阻，电感和电容，它们相对于电流和电压保持恒定。对于任何给定的输入，任何线性电路（无论是电阻性，电感性还是电容性）都具有成比例的输出。线性响应表示流经任何支路的电流和跨任何组件的压降。

叠加定理具有超级Duper等级

叠加通过分压，分流，串并联组合和欧姆定律发生。为了分析每个信号源对电路的影响，我们必须将其他信号源的所有值都设置为零。我们可以通过将每个电压源替换为短路并将每个电流源替换为开路来实现此目的。在考虑了每个源之后，我们可以通过叠加每个分量电流或电压来发现一个元件的总电流或电压。

我们可以使用叠加定理找到图1所示电路中流动的电流。

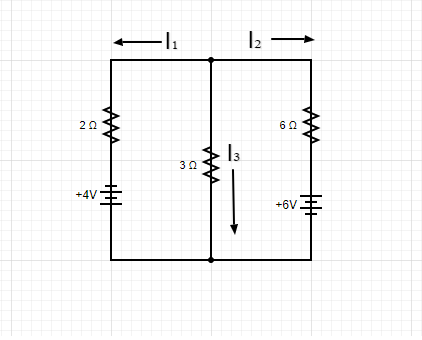
图一

从左手源引起的电流开始，我们可以获得几个电流。电路中的总电阻（RT）等于：

RT = 2 +（3 x 6）/ 9 =4Ω和

I4 = 4v /4Ω= 1A

如图2所示，我们可以使用电流除法来继续增加两个电流值：

I5 =（6/9）x I4 = 0.667A，I6为

I6 = 0.333安

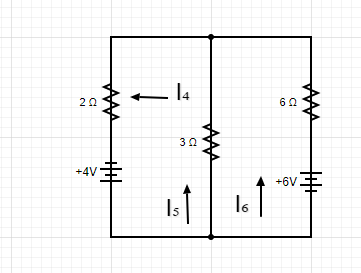
图二

求解左侧电源后，我们可以确定右侧电源的电流。如图三所示，RT =

6 +（2 x 3）/ 5 = 6 + 1.2 =7.2Ω

而

I7 = 6 v /7.2Ω= 0.833A

再次使用电流分配，我们可以确定I8和I9电流的值。

I8 =（2/5）x I7 = 0.333A

I9 = 0.5A

从那里，我们可以确定流过2Ω电阻的电流。

I1 = I4 + I9 = 1.0 + 0.5 = 1.5A

以及I2和I3的值

I2 = -I6 – I7 = -0.333 – 0.833 = -1.166A

I3 = -I5 + I8 = -0.667 + 0.333 = -0.334A

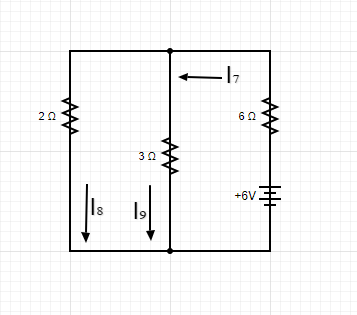
图三

超人有时也会失去力量

rypto定理的石是仅当电压，电流和电阻之间存在线性关系时才适用。由于电阻器中的功率损耗是由平方关系产生的，因此我们可以通过叠加功率损耗来计算功率。相反，我们必须根据总电压或电流值来计算功率。以图1中的2Ω电阻为例，该电阻的功率不等于：

P = ［（I2 + I4）x 2］ + ［I2 + I9 x（1）2 x 2］ + 0.52 x 2 = 2 + 0.5 = 2.5瓦

相反，我们必须使用以下计算来确定2Ω电阻的功率。

P =（I2 x I1）x 2 = 1.52 x 2 = 4.5瓦

验证对于任何电路设计都很重要。作为电路设计工程师和设计团队，为了使您的电子产品尽可能少地出现错误或漏洞，将其投入生产，与电路仿真工具保持紧密联系是至关重要的。了解叠加定理会有所帮助；但是，拥有可以在整个设计过程中为您准确可靠地模拟这些结果的工具非常宝贵。
编辑：hfy