了解内存：如何在嵌入式C语言中使用结构

处理器如何访问内存？了解有关C语言结构以及如何使用它们的更多信息。
本文将首先解释内存访问粒度的概念，以便我们可以对处理器如何访问内存有一个基本的了解。然后，我们将仔细研究数据对齐的概念，并研究一些示例结构的内存布局。

在上一篇有关嵌入式C中的结构的文章中，我们观察到重新排列结构中成员的顺序可以更改存储结构所需的内存量。我们还看到，当为结构的成员分配内存时，编译器具有某些约束。这些被称为数据对齐要求的约束条件允许处理器以可能在内存布局中出现的一些浪费空间（称为“ 填充 ”）为代价更有效地访问变量。

本文将首先解释内存访问粒度的概念，以便我们可以对处理器如何访问内存有一个基本的了解。然后，我们将仔细研究数据对齐的概念，并研究一些示例结构的内存布局。

值得一提的是，计算机的存储系统可能比这里介绍的复杂得多。本文的目的是讨论一些对嵌入式系统进行编程时可能有用的基本概念。

内存访问粒度

我们通常将内存设想为单字节存储位置的集合，如图1所示。这些位置中的每一个都有一个唯一的地址，该地址使我们可以访问该地址的数据。


图1
但是，处理器通常以大于一个字节的块的形式访问内存。例如，处理器可以按四个字节的块访问内存。在这种情况下，我们可以设想图1的12个连续字节，如下图2所示。


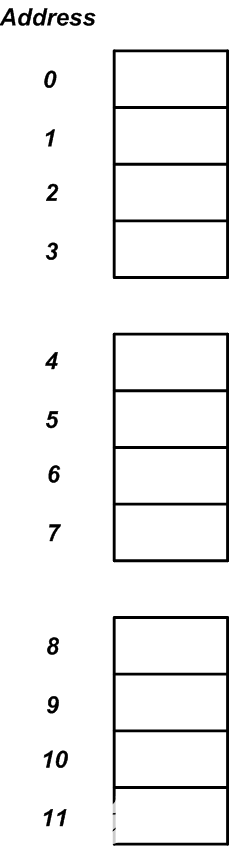
图2
您可能想知道这两种处理内存的方式有何区别。在图1中，处理器一次读取一个字节并将其写入内存。请注意，在读取或写入存储器位置之前，我们需要访问该存储器单元，并且每次访问存储器都需要一段时间。假设我们要读取图1中的内存的前八个字节。对于每个字节，处理器都需要访问内存并读取它。因此，要读取前八个字节的内容，处理器将必须访问存储器八次。

使用图2，处理器一次从存储器中读取和写入四个字节。因此，为了读取前四个字节，处理器访问存储器的地址0，并读取四个连续的存储位置（地址0至3）。同样，要读取下一个四个字节的块，处理器需要再访问一次内存。它转到地址4，并同时从地址4到7读取存储位置。对于字节大小的块，需要八个内存访问才能读取八个连续的内存字节。但是，对于图2，仅需要两次内存访问。如上所述，每次内存访问都需要一些时间。由于图2所示的内存配置减少了访问次数，因此可以提高处理效率。

处理器访问内存时使用的数据大小称为内存访问粒度。图2描述了具有四字节内存访问粒度的系统。

内存访问边界
硬件设计人员经常采用另一项重要技术来使处理系统更高效：他们限制处理器，使其只能在特定边界访问内存。例如，处理器可能只能在四字节边界访问图2的内存，如图3中的红色箭头所示。


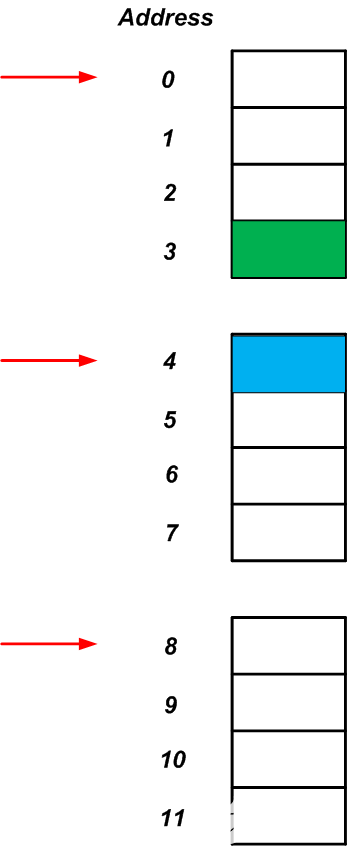
图3
这种边界限制会大大提高系统效率吗？让我们仔细看看。假定我们需要读取地址为3和4（由图3中的绿色和蓝色矩形表示）的存储单元的内容。如果处理器可以从任意地址开始读取四字节的块，我们可以访问地址3并通过一次内存访问来读取两个所需的内存位置。但是，如上所述，处理器不能直接访问任意地址。相反，它仅在特定边界访问存储器。那么，如果处理器只能访问四个字节的边界，那么它将如何读取地址3和4的内容呢？

由于内存访问边界的限制，处理器必须访问地址为0的内存位置并读取四个连续的字节（地址0至3）。接下来，它必须使用移位操作将地址3的内容与其他三个字节（地址0到2）分开。类似地，处理器可以访问地址4并从地址4到7读取另一个四字节的块。最后，可以使用移位操作将所需的字节（蓝色矩形）与其他三个字节分开。

如果没有内存访问边界限制，我们可以通过一次内存访问读取地址3和4。但是，边界限制迫使处理器两次访问内存。那么，如果它使数据操作更加困难，为什么还要将内存访问限制在某些边界呢？存在内存访问边界限制是因为对地址进行某些假设可以简化硬件设计。例如，假设需要32位来寻址内存块中的所有字节。如果我们将地址限制为四字节边界，则32位地址的两个最低有效位将始终为零（因为该地址将始终被4整除）。因此，我们将能够使用30位来寻址2 32字节的内存。

数据对齐
既然我们知道基本处理器如何访问内存，我们就可以讨论数据对齐要求。通常，任何K字节的C数据类型都必须具有K的倍数的地址。例如，四字节的数据类型只能存储在地址0、4、8，…；不能将其存储在地址1、2、3、5，...。这样的限制简化了处理器和存储系统之间接口硬件的设计。

例如，考虑具有四字节内存访问粒度的处理器，该处理器只能在四字节边界访问内存。假设有一个四字节变量存储在地址1中，如图4所示（这四个字节对应于四种不同的颜色）。在这种情况下，我们将需要两次内存访问和一些额外的工作才能读取未对齐的四字节数据（“ 未对齐 ”是指将其拆分为两个四个字节的块）。该过程如图所示。


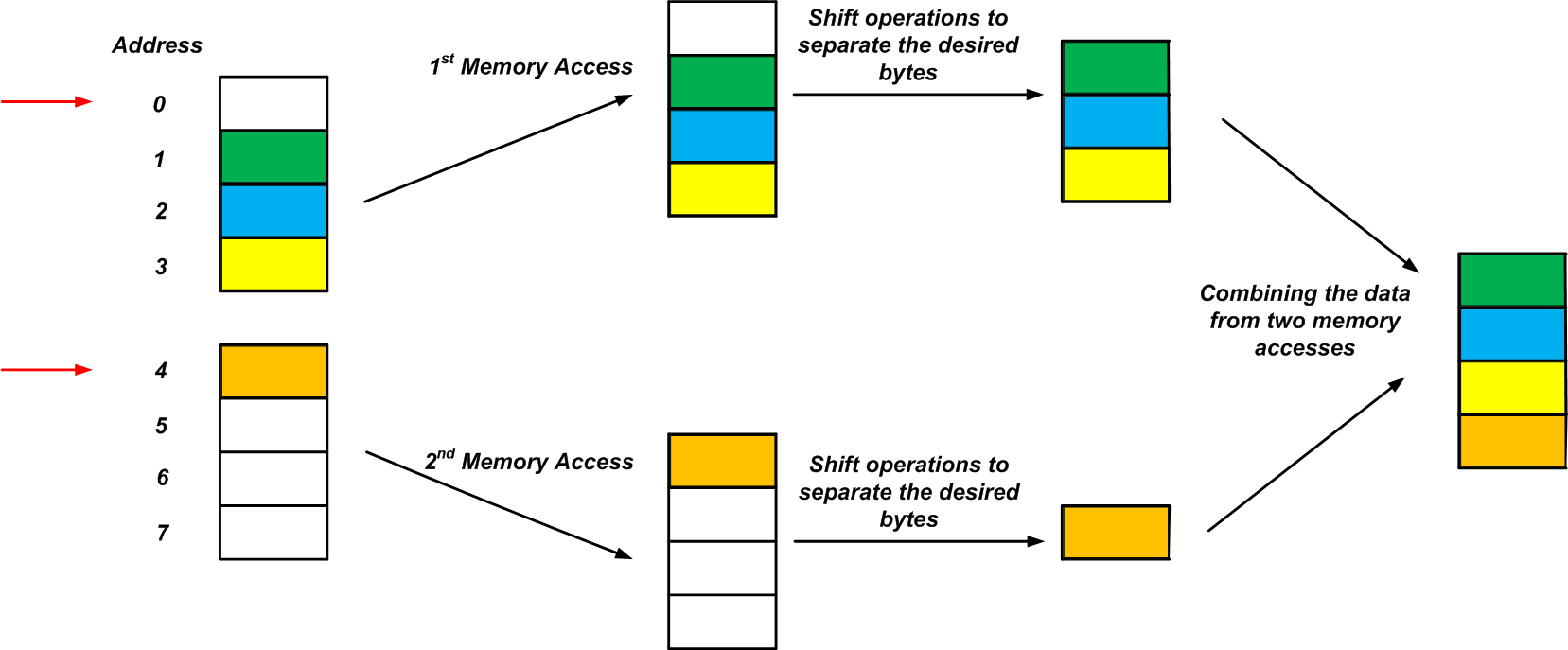
图4
但是，如果我们将四字节变量存储在4的倍数的任何地址上，则只需要一次内存访问即可修改数据或读取数据。

这就是为什么将K字节数据类型存储在K的倍数的地址可以使系统效率更高的原因。因此，可以将C语言“ char ”变量（仅需要一个字节）存储在任何字节地址，但是必须将两个字节的变量存储在偶数地址。四字节类型必须从可被4整除的地址开始，八字节数据类型必须被存储在被8整除的地址中。例如，假设在特定计算机上，“ short ”变量需要两个字节，“ int ”和“ float ”类型占用四个字节，而“ long ”，“ double””，而指针占据八个字节。这些数据类型中的每一个通常都应具有K的倍数的地址，其中K由下表给出。

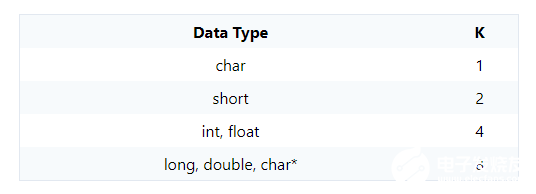
请注意，不同数据类型的大小可能会因编译器和计算机体系结构而异。sizeof（）运算符将是查找数据类型的实际大小的最佳方法。

结构的内存布局

现在，让我们检查一下结构的内存布局。考虑为32位计算机编译以下结构：

struct Test2{

        uint8_t            c;
        uint32_t    d;
        uint8_t            e;
        uint16_t    f;

} MyStruct;

我们知道将分配四个内存位置以在结构中存储成员，并且内存位置的顺序将与声明成员的顺序匹配。第一个成员是一个字节的变量，可以存储在任何地址。因此，第一个可用的存储位置将分配给该变量。假定如图5所示，编译器将地址0分配给该变量。下一个成员是四字节数据类型，只能存储在4的倍数的地址上。第一个可用的存储位置是地址4。但是，这需要保留地址1、2和3未被使用。如您所见，数据对齐要求导致了内存布局中一些浪费的空间（或填充）。

下一个成员是e，它是一个一字节的变量。可以将第一个可用的存储位置（图5中的地址8）分配给该变量。接下来，我们到达f，它是一个两个字节的变量。可以将其存储在可被2整除的地址中。第一个可用空间是地址10。如您所见，将出现更多的填充以满足数据对齐要求。


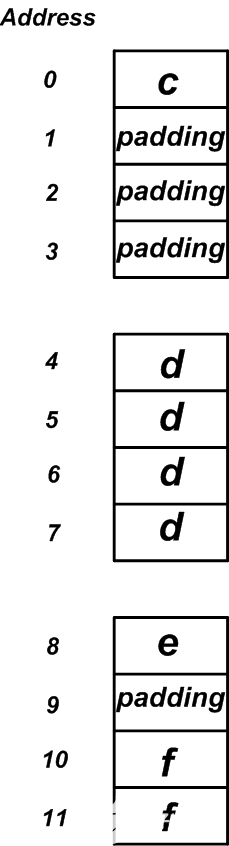
图5

我们希望该结构占用8个字节，但实际上需要12个字节。有趣的是，如果我们了解数据对齐要求，则可以重新排列结构中成员的顺序，并提高内存使用效率。例如，让我们重写下面的结构，其中成员从最大到最小排列。

struct Test2 {
   
     uint32_t       d;
     uint16_t       f;
     uint8_t        c;
     uint8_t        e;
   
} MyStruct;

在32位计算机上，上述结构的内存布局可能类似于图6中所示的布局。


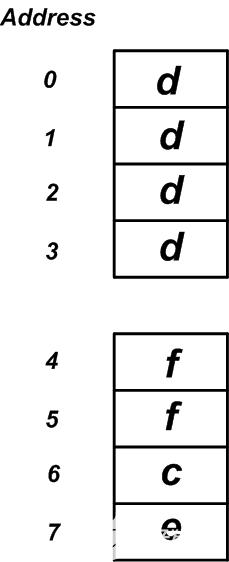
图6
第一个结构需要12个字节，而新结构仅需要8个字节。这是一项重大改进，尤其是在内存受限的嵌入式处理器的情况下。

另外，请注意，结构的最后一个成员之后可能会有一些填充字节。结构的总大小必须被其最大成员的大小整除。考虑以下结构：

struct Test3 {
   
        uint32_t     c;
        uint8_t      d;
                
} MyStruct2;

在这种情况下，内存布局将如图7所示。您可以看到，在内存布局的末尾添加了三个填充字节，以将结构的大小增加到8个字节。这将使结构大小可被结构中较大成员（c成员，这是一个四字节的变量）的大小整除。


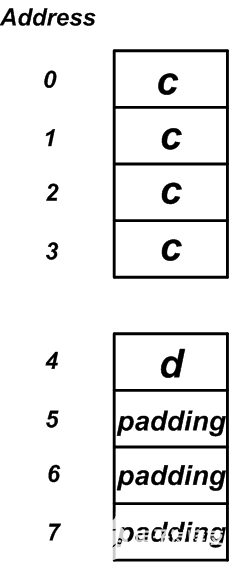
图7

概要
 

• 处理器通常以大于一个字节的块的形式访问内存。这样可以提高系统效率。

• 处理器访问内存时使用的数据大小是处理器的内存访问粒度。

• 处理器可能被限制为仅在某些边界（例如，在四字节边界）访问存储器。

• 存在此内存访问限制是因为对地址进行某些假设可以简化硬件设计。

• 通常，任何K字节的C数据类型都必须具有K的倍数的地址。此类限制简化了处理器与内存系统之间接口硬件的设计。

• 数据对齐要求导致内存布局中的某些空间浪费（或填充）。

• 结构的最后一个成员之后可能会有一些填充字节。结构的总大小必须被其最大成员的大小整除。