

利用非完全补偿技术实现超高增益带宽,并降低输入电压噪声
模拟技术
描述
对直流耦合脉冲放大器来说,设计人员要想获得高压摆率和低噪声,通常就必须采用增益带宽极高、非单位增益稳定的电压反馈运算放大器。这类运放由于其内部补偿电容较低,因此获得了“非完全补偿(decompensated)”的绰号,并可以提高压摆率,同时,由于其输入级跨导gm较高,因此可以实现超高增益带宽,并降低输入电压噪声。
不幸的是,许多设计人员在试图将这些敏感的非完全补偿器件用于低增益时都事与愿违。与高增益带宽电压反馈设计相比,电流反馈拓扑因其优异的压摆率和低增益稳定性而受到欢迎。然而,电流反馈运放虽然具有优异的高频性能,但是却具有较差的直流精度和较高的输出噪声。
运放设计人员推荐了各种形式的外部补偿,以便利用非完全补偿电压反馈运放在低信号增益时的直流精度、低噪声和高压摆率。然而,之前推荐的补偿方案存在很多缺点。例如,一些运放可以访问内部补偿节点,但增加这个主导极点补偿会直接降低压摆率。常见的超前滞后补偿技术在闭环响应中会产生零极点对,从而导致糟糕的脉冲响应和建立特性。
一种新的外部补偿方法可以在低信号增益下实现对简单二阶低通响应的完全控制。这种技术对任何内部非完全补偿的运放来说,都可以在任何反相增益下实现良好控制的频率响应。非完全补偿运放的输出端可实现最大压摆率,同时输出噪声电压密度随频率的增加而增加。此输出噪声增加是因为噪声增益中必须要有峰值,才能实现平坦的闭环频率响应。无源后置滤波可以显著降低此噪声的影响。
将这种外部技术与高质量的非完全补偿电压反馈运放一起使用,所实现的绝对直流精度要远优于高速电流反馈方案。与等效电流反馈方案相比,其噪声和压摆率相当,谐波失真会低得多。再做些额外工作,就可以使用这种补偿来仿真电流反馈运放的增益带宽无关性。使用电压反馈运放实现的增益带宽无关性对于反相求和应用非常有用,这样就可以在设计过程中很方便地调整求和权重。
一旦了解了其拓扑并推导出基本的传递函数,就可以根据所需的信号增益和放大器的特性来预测放大器的性能。有三个设计实例可说明该补偿技术是如何最大程度提高可达平坦带宽,实现滤波器,或创建增益带宽无关的设计(以及为什么会需要它)。
分析补偿电路
该补偿技术非常简单,只需在标准的反相运放中增加两个补偿元件CS和CF(图1)。以前有关此电路的讨论都集中在使用CF来补偿寄生CS上。下述分析将重点说明应如何设置CS和CF,才能在任何信号增益下,甚至对于补偿程度最低的运放也能获得控制良好的闭环二阶低通频率响应。
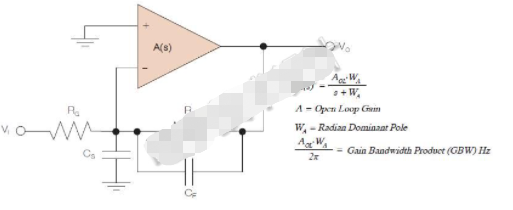
图1:由CF和CS组成的简单但以前从未探索过的补偿电路。利用这种技术,就可在低增益时使用非完全补偿电压反馈运放,来获得电流反馈运放的高频优势和电压反馈器件的直流精度。
利用运放的单极点开环模型可以很容易分析此电路。如果没有CS和CF,单极点运放模型就不适合,因为非完全补偿运放的高阶极点完全决定低增益时的闭环响应。但是,使用补偿元件,就可以将其简化为单极点设计。
反相配置是这种补偿工作的唯一方式,除此之外,它还具备其他一些优点。由于V+输入端没有共模信号摆动,因此大多数运放的反相配置可实现高压摆率、高全功率带宽和低失真。这种反相模式有很多好处,但也会付出代价,即RG会引起输入阻抗,运放的同相输入电压噪声所遇直流噪声增益会变高一点。
图1中的电路可以以波特图分析形式写出拉普拉斯传递函数:
(1)
其中
(2)
(3)
且单极点运放的开环增益为
(4)
该传递函数的关键组成部分包括:
1. ZF/RG,理想运放(具有无限开环增益和带宽)的信号增益;
2. 1+ZF/ZG,环路增益的噪声增益部分(也等于从同相输入到输出的增益);
3. A(s),运放随频率变化的开环增益。
在直流情况下,公式1中的分母约等于1,分子等于-RF/RG,这是期望得到的低频信号增益。我们通常靠查看相应的波特图(如图2所示)来进行稳定性分析。波特图的幅度部分将噪声增益的幅度与开环增益的幅度进行比较,分别是公式1分母中分数的上部和下部。在这两条曲线交叉处(即环路增益交越点处)的频率,环路增益下降到1V/V(0dB),而在简单的运放应用中,闭环带宽发生滚降。由于公式1的分子中还包含一个极点,因此这种简单的分析不足以确定闭环响应。
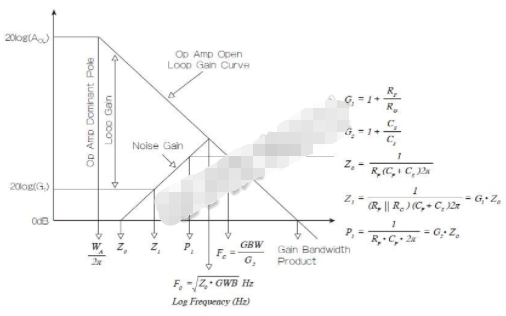
图2:对于补偿网络设计,波特图分析指出了噪声增益曲线倾斜部分的单位增益交点(Z0)、由反馈补偿网络设定的极点(P1)、低频噪声增益(G1),以及环路增益交越处的噪声增益(G2)。
通常还需要考虑环路增益项的相位。但是,公式1最终可简化为简单的二阶低通传递函数,可以通过控制该传递函数的ω0和Q来继续设计。从波特图分析中的幅度部分可以了解到设计中会发生什么,但不能用该幅度信息设置CS和CF。现在,假设环路增益交越发生在噪声增益足够高的位置——这样就可以安全忽略掉A(s)的高阶极点——那么就可以忽略相位图。
将两个阻抗值ZF和ZG以及运放的开环增益表达式A(s)代入公式1,得到:
(5)
调整这个公式,将分母中的噪声增益项表达为零极点的形式,得到:
(6)
分母中的各项构成该传递函数的开环增益部分。运放的开环增益具有高直流值的AOL和主导极点ωA。噪声增益具有1+RF/RG的直流增益、低频零点和高频极点,可在较高频率下将噪声增益变平至1+CS/CF。图2所示的完整波特图显示了此环路增益的增益幅度部分,以及对设计至关重要的一些关键频率。
这些关键频率(以Hz表示)包括GBP、Z0和P1。GBP就是所选运放的增益带宽积(GBP=AOLωA/2π Hz)。Z0等于1/[2πRF(CS+CF)],是噪声增益曲线倾斜部分的单位增益(0dB)交点。噪声增益的实际零点出现在G1Z0=Z1处。G1和G2分别为低频和高频噪声增益。
P1是反馈网络的极点,等于1/(2πRFCF)。调整该极点和Z0可以控制闭环频率响应。P1还等于Z0G2,即Z0乘以由电容器比率所确定的高频噪声增益。
图2中另一个令人感兴趣的点是噪声增益曲线倾斜部分的投影与开环增益曲线在Z0和GBP的几何平均值处的交点。这个点即为闭环二阶响应的特征频率F0(见附录:二阶低通响应特性)。当将P1设置为小于此几何平均值时,噪声增益曲线与开环响应曲线以G2的增益相交。噪声增益与开环响应的交点为FC,它将等于具有相同GBP且以同相噪声增益G2工作的单位增益稳定运放的闭环带宽。
此分析的一个关键假设是可以控制G2的值,使其大于运放指定的最小稳定增益。正因为是以这一高噪声增益发生交越,才能以-RF/RG的低信号增益使用非单位增益稳定运放。但是,运放制造商对最小稳定增益的定义没能达成一致。一些制造商使用典型的相位裕度目标,其他制造商则使用最大峰值,还有一些制造商则实际指定引起闭环响应发生振荡的增益。通常,大多数数据手册均会推荐一个不会引起振荡的最小增益值。本设计的目标是使环路增益以足够高的G2噪声增益与开环响应相交,从而可以安全忽略掉A(s)的高阶极点。如果数据手册上的最小稳定增益确实是推荐的最小工作值,那么将交越点定在该增益的1.5倍应该是安全的。当然,这个安全区只是一个估计值,它会因元件和制造商的不同而异。大多数制造商都提供宏模型,可以用它来微调这个值。
可以广泛使用波特图中的频率和增益,深入了解二阶闭环传递函数的代数解。由于该设计要求出补偿元件(CF和CS)的值,以下方法采用角频率单位。将此单位转换为图2所示的赫兹,只需要除以2π。
将公式6的传递函数扩展为标准的首一形式(即按最高次项到最低次项写多项式,且最高次项系数为1),可以得出:
(7)
其中
(8)
且
(9)
尽管这一完整的传递函数最终变成二阶低通响应,看起来可喜可贺,但算式的每一项看上去却仍然有点棘手。通过一些处理和谨慎的简化,可以得出 ω0和Q的简单表达式,而清晰地反映设计方法。
具体来说,如果认识到AOL远大于1+RF/RG,就可以简化ω0根号内部。去掉1+RF/RG算式项,根据 AOLωA=GBP和1/((CF+CS)×RF)=Z0(见图2),简化分母中Q的表达式,就可以得到以下公式,其中G2=1+CS/CF,G1=1+RF/RG:
(10)
且
(11)
再回头参考图2中的波特图,这些简单的公式表明二阶闭环响应的特征频率为ω0,即Z0和放大器GBP的几何平均值。此外,该特征频率与高频环路增益交越频率(FC)和噪声增益(Z1)零频率之和的比值确定了Q值。如果已经选定放大器和所需的信号增益(G1=|SIGNAL GAIN|+1),则只需设置Z0和P1(或等效的G2)即可实现补偿。
责任编辑:gt
-
噪声增益到底是什么意思?2024-11-29 11610
-
陷波滤波器可降低放大器峰值并增加增益平坦度2023-02-01 3856
-
高增益与高带宽要怎么样才能兼得2021-11-19 2737
-
OPA699是宽带高增益限压放大器2020-09-18 1581
-
如何对放大器进行补偿以在较低增益下工作2019-12-07 2689
-
高增益低噪声的探测器读出电路设计2018-11-12 2365
-
高增益与高带宽怎么兼得?2018-09-21 2583
-
高增益与高带宽怎么兼得2018-09-20 1894
-
示波器的带宽增强技术2018-04-03 3083
-
高增益与高带宽电路设计,如何实现?2017-04-08 6257
-
并馈全向高增益天线的研制2011-12-26 819
-
基于AD603数控高增益宽带放大器的设计2010-05-04 4789
全部0条评论

快来发表一下你的评论吧 !

