《物理》2020年第9期：两只“量子柴郡猫”笑脸的无接触交换

本文选自《物理》2020年第9期

01    理论背景        

在经典世界中，物体都拥有丰富的属性，如质量、体积等等。可以说，正是对这些属性的认识和描述，在人们脑海中形成各种各样客观实在的物理图像。对客观存在的物体的各种属性及其相互联系和运动规律的研究，构成了我们今天的物理学。直觉告诉我们，物理本体与其拥有的属性是不可分离的[1]。然而，这个直觉源自对经典世界中物理客体的认识，并严重依赖于经典物理图像。当我们将视角聚焦到微观尺度，研究半径只有不到一个皮米(10-12 m)的电子或是波长不到一个微米(10-6 m)的光子时，情况就变得有所不同。2013年有理论研究认为，微观粒子的物理属性(如电子的电荷和自旋、光子的偏振等)可以和其本体分离，这种现象被沃尔夫奖获得者阿哈罗诺夫等人称之为“量子柴郡猫”(quantum Cheshire cat)[2]。

02    弱测量与弱值        

为了揭示微观世界中的“量子柴郡猫”现象，需要使用有别于传统量子测量的手段，也就是量子弱测量技术。这里之所以被冠以“弱”，是相对于传统量子测量表现出的“强”而言的。在传统的量子测量理论中，测量用可观测量算符表示[3]。对描述微观系统的波函数实施的量子测量，会将系统随机坍缩到测量算符的某一个本征态[4]，这个过程将不可避免地破坏量子系统的状态。例如使用检偏器对光子的偏振状态进行鉴定，尽管最终能够确定光子的偏振方向，但同时也会完全破坏初始状态，除非光子一开始就处在检偏器的本征指向上。在该测量过程中，正是由于需要完成待测量子系统和测量探针之间足够强的耦合，以至于能将系统和探针完全纠缠起来，我们将其称之为强测量。

与之相对应，量子弱测量则考虑另外一种情况，那就是系统和探针之间的耦合非常微弱，以至于被测系统和探针仍然处于接近独立的状态。如此弱的耦合不会对系统造成演化过程的过分干扰，系统还可以继续完成后续相干演化，但同时弱测量也不会提供关于系统状态的确定性信息。作为量子力学中一个比较古老的话题，直到弱值概念被提出后，弱测量才开始受到应有的关注[5]。和量子强测量中定义可观测量的期望值一样，可观测量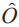的弱值被定义在前选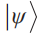择态和后选择态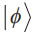上，由两者共同决定，即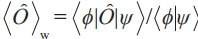。但有别于传统期望值，弱值并不局限于在可观测量本征值上进行取值，可以远超过这个范围，甚至可以取复数值。无论是面向量子信息开发新技术还是探索量子力学基本问题，弱测量和弱值的概念都被广泛采用：在技术层面，如开发基于白光源的高精度时间延迟测量[6，7]，以及直接表征纠缠系统波函数[8]等；而在基础研究层面，如重构微观粒子的玻姆轨迹[9]，以及观测杨氏双缝中非局域的动量传递[10]等。 

03    概念提出与实验验证        

回到如何揭示“量子柴郡猫”这个问题，在其最初版本中，阿哈罗诺夫等人考虑将光子作为“量子柴郡猫”，并且将光子的自旋(偏振)作为其笑脸[2]。简化示意如图1所示，其中包括分束器、反射镜及探测器等。整个系统由一个 Mach—Zehnder 干涉仪构成，其中光子在经过分束镜后，可以选择上下两个路径。我们可以通过对光子实施两组弱测量来揭示光子本体和其属性的分离，其中一组用于测量光子本体所处的位置(用路径可观测量 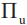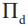，表示)，另一组则用于测量其自旋状态，也就是柴郡猫的笑脸(用条件自旋可观测量，表示)，测量结果则由相应的弱值描述。当某个路径可观测量的弱值为1时，表明光子本体出现在相应的路径当中，取值为0则表明光子本体未处于相应的路径当中；类似地，条件自旋投影子的弱值为 1/0 则表明光子的自旋(笑脸)出现/未出现在相应的路径中。阿哈罗诺夫等人指出，通过精巧设置合适的前后选择态，就有可能展现类似《爱丽丝梦游仙境》中柴郡猫与其笑脸分离的现象[11]。具体来说，在 Mach—Zehnder 干涉仪的上路径中，对路径及条件自旋观测量实施的弱测量给出相应的弱值分别为0和1，也就是说，有一只没有猫的笑脸出现在该路径中。相应的，在下路径中实施的弱测量得到的弱值分别为1和0，也就是说，下路径中出现了一只缺少了笑脸的猫。简而言之，在干涉仪中“量子柴郡猫”和它的笑脸被分开了。

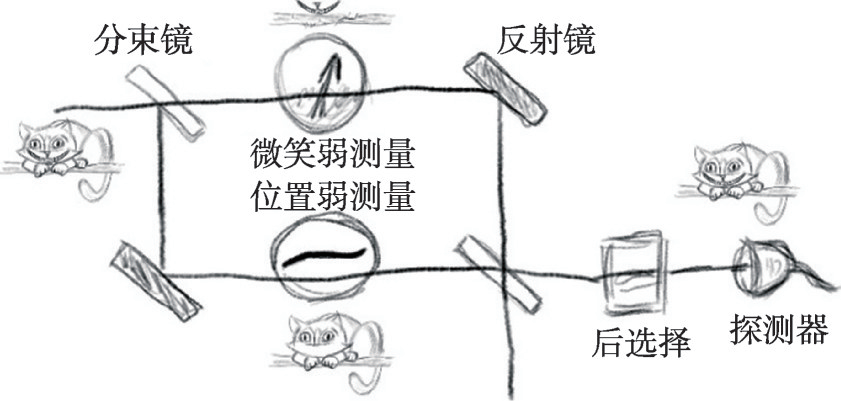
图1 由 Mach—Zehnder 干涉仪构成，揭示“量子柴郡猫”效应的示意图

在“量子柴郡猫”的概念被提出后不久，来自奥地利维也纳科技大学的实验物理学家便利用中子进行了实验演示[12]。他们通过在中子干涉仪中外加磁场，精确调控中子的自旋和路径的量子状态，从而实现了前选择态的制备以及后选择的操作。在干涉仪的两臂中施加弱测量获得所需要的中子路径及条件自旋的弱值。实验结果正如阿哈罗诺夫等人所预言的那样，在干涉仪中，中子的自旋总是出现在与其本体位置相反的另一臂。紧接着，美国波特兰大学的实验物理学家使用自发参量下转换过程产生的可预报单光子进行了类似的实验，同样看到了“量子柴郡猫”现象[13]。 

04    缺陷与争议        

这些实验进展表明，不论是有质量的中子还是无质量的光子，都能展现出这种不符合常理却真实存在的量子现象。然而，利用光子进行的实验备受争议，因为这种现象在基于经典光的干涉仪中同样能够观察到，并且这样的实验可以用描述电磁波的经典波动理论予以解释[14]。因此，“量子柴郡猫”在多大程度上是属于量子世界，这一问题亟需得到确认。另一方面，既有实验尽管展示了微观粒子在演化过程中可以处于本体与属性的分离，但是最终它们仍然聚合到了一起。既然物理属性可以从其本体分离，随之也自然会带来如下问题：物理客体是否可以携带本不属于自己的物理属性呢[15]？因此，进行更为复杂的实验进一步展示“量子柴郡猫”的独特量子效应，例如实现涉及多个“量子柴郡猫”笑脸的交换，可以从正面回答这两方面的争议，对理解量子系统如何从根本上区别于其经典对应具有重要的物理意义。

05    笑脸的隔空交换        

然而，尝试观察“量子柴郡猫”的笑脸交换并不容易，这涉及到对多体量子系统弱值提取的难题[16—18]。提取弱值的通常做法是引入辅助探针，当系统增大时，所需的耦合过程将会越来越复杂。想要实现光子偏振的无接触交换，势必涉及多个“量子柴郡猫”，进一步在系统中引入额外探针面临技术挑战。我们经过理论研究发现，通过对系统施加微扰，可以绕过传统的弱测量方法，利用系统探测概率与微扰强度之间的内在联系，直接得到所需要的弱值[19]。此外，我们还发现获得弱值所需的微扰形式，与数学中的虚数概念有着深刻的联系。在量子力学中，一个封闭体系的演化遵循薛定谔方程，时间是演化的一个参数。如果将演化的时间取为一个绝对值很小的虚数，对应的微扰将使体系不再封闭，但是这种演化恰好可以将光子最后被测量的概率与演化的时间联系起来，在两者之间建立一个线性的关系。这个线性模型的斜率就刚好给出弱值，而相应的微扰被称之为虚时演化[20]。

图2 实现“量子柴郡猫”笑脸交换的实验装置。包括3个模块：基于自发参量下转换的双光子超纠缠态制备，使用平行偏振分束器实现条件自旋可观测量弱测量的装置，以及实现笑脸交换的双光子干涉光路(改编自文献[19])

如图2所示，我们首先通过自发参量下转换过程，制备出不存在经典描述的双光子超纠缠态，也就是两个光子的偏振和路径自由度分别处于最大纠缠态，但是两个维度之间处于毫无关联的直积状态。进一步通过在路径和自旋上施加一些精确的受控操作，将双光子制备到特定图态，完成前选择态的制备。紧接着，我们通过在光路中引入虚时演化，实现对光子路径和条件自旋的弱测量。在实验的最后，通过实施一种被称为联合贝尔态测量的操作，完成对系统的后选择。我们通过对不同的微扰种类和演化时间下光子探测效率地分析，最终获得了光子的路径和条件偏振可观测量的弱值。实验的主要结果如图3所示。这些弱值表明，实验中的两光子都展现出本体和属性分离的“量子柴郡猫”现象。更为重要的是，最终每只量子柴郡猫都会捕获另一只猫的偏振属性。这个新捕获的偏振替代了光子原先的偏振属性，随着光子最终进入探测器而被检测到，最终实现光子本体与其初始时刻携带的自旋属性的永久分离。

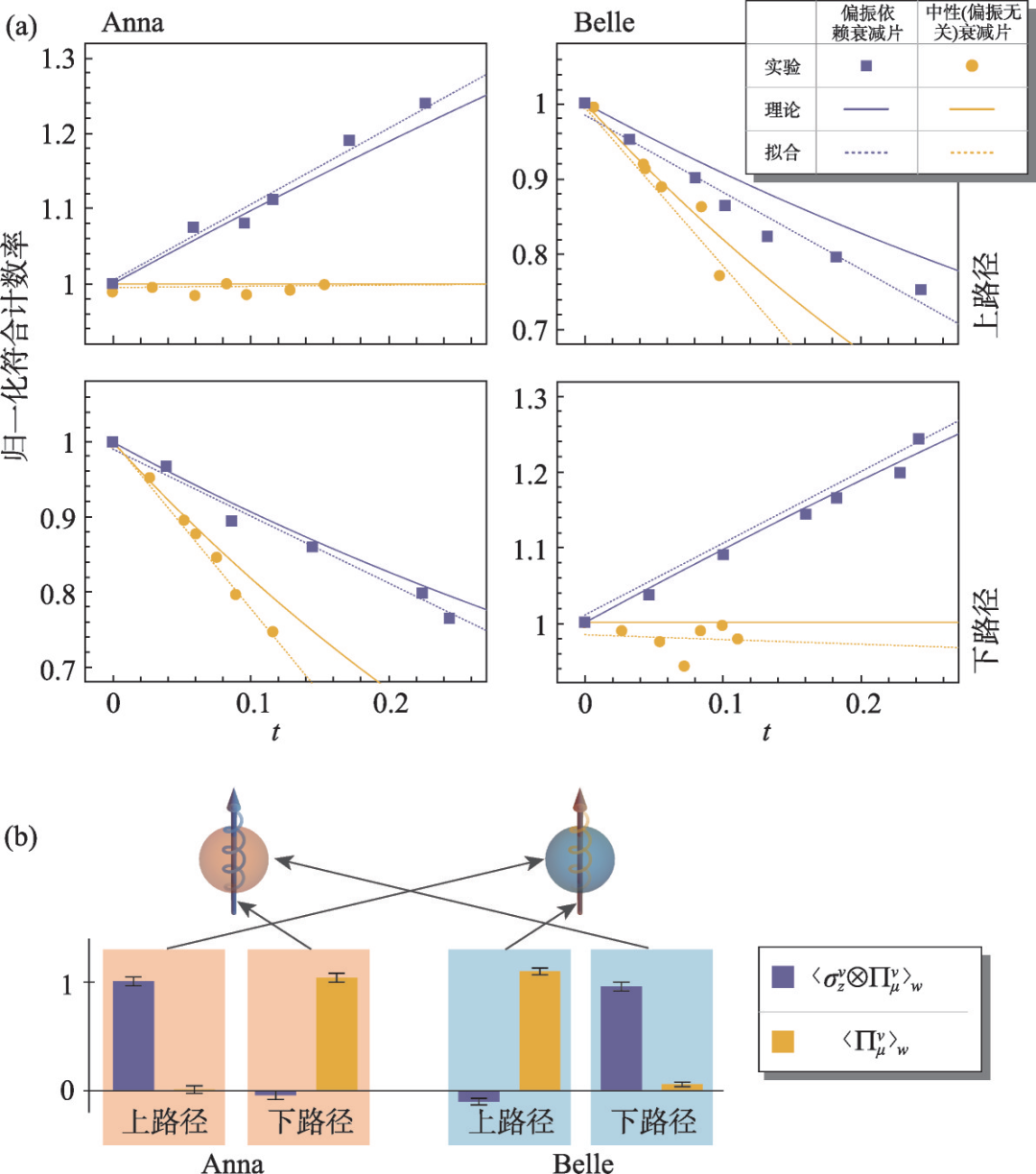
图3 归一化符合计数随耦合时间线性变化(a)，其斜率给出相应可观测量的弱值(b)。其中Anna和Belle是两只柴郡猫的名字(改编自文献[19])

该研究成果最近发表在《自然·通讯》[19]。实现多个“量子柴郡猫”的笑脸交换，展示了量子世界中物质与其属性的灵活多变的关系，对探索微观粒子的性质在接受测量之前是否具有实在性(真实，reality)具有启发意义，将对量子力学基础问题的研究起到重要推动作用。另一方面，通过引入微扰获得弱值，从而规避传统方法对额外辅助探针的需求，也将成为解决量子科学领域其他难题的有力工具。

参考文献

[1] Bancal J D. Nat. Phys.，2013，10：11

[2] Aharonov Y，Popescu S，Rohrlich D et al. New J. Phys.，2013，15：113015

[3] Griffiths D J. Introduction to quantum mechanics. Cambridge University Press，2016

[4] von Neumann J. Mathematical foundations of quantum mechanics. Princeton University Press，2018

[5] Aharonov Y，Albert D Z，Vaidman L. Phys. Rev. Lett.，1988，60：1351

[6] Xu X Y，Kedem Y，Sun K et al. Phys. Rev. Lett.，2013，111：033604

[7] Li C F，Xu X Y，Tang J S et al. Phys. Rev. A，2011，83：044102

[8] Pan W W，Xu X Y，Kedem Y et al. Phys. Rev. Lett.，2019，123：150402

[9] Xiao Y，Kedem Y，Xu J S et al. Opt. Express，2017，25：14463

[10] Xiao Y，Wiseman H M，Xu J S et al. Sci. Adv.，2019，5：eaav9547

[11] Carroll L. Alice's adventures in wonderland. Broadview Press，1865

[12] Denkmayr T，Geppert H，Sponar S et al. Nat. Commun.，2014，5：4492

[13] Ashby J M，Schwarz P D，Schlosshauer M. Phys. Rev. A，2016，94：012102

[14] Atherton D P，Ranjit G，Geraci A A et al. Opt. Lett.，2015，40：879

[15] Das D，Pati A K. New J. Phys.，2020，22：063032

[16] Kedem Y，Vaidman L. Phys. Rev. Lett.，2010，105：230401

[17] Xu X Y，Pan W W，Wang Q Q et al. Phys. Rev. Lett.，2019，122：100405

[18] Xu X Y，Pan W W，Kedem Y et al. Opt. Lett.，2020，45：1715

[19] Liu Z H，Pan W W，Xu X Y et al. Nat. Commun.，2020，11：3006

[20] Xu J S，Yung M H，Xu X Y et al. Nat. Photonics，2014，8：113

责任编辑：xj

原文标题：两只“量子柴郡猫”笑脸的无接触交换

文章出处：【微信公众号：中科院半导体所】欢迎添加关注！文章转载请注明出处。