

介绍正态分布在电气工程中的位置
描述
本文介绍了基础统计分布的重要特征,并说明了概率密度函数的重要性。
本文是我们关于电气工程统计的系列文章的续篇。前两篇文章讨论了统计分析和统计性描述,为我们的讨论奠定了基础。
然后,我们研究了信号处理中的平均偏差,标准偏差和方差-在计算标准偏差时要特别注意样本量补偿。在上一篇文章中,我们通过探索标准差与均方根值的关系来进一步推断我们对标准差的理解。在本文中,我们将介绍正态分布在电气工程中的位置,特别是在评估概率密度函数中。
什么是正态分布?
如果您反复测量一个或多或少随机变化的量(噪声信号中的电压电平,47kΩ电阻器的实际电阻值,工程等级的测试分数,草坪上的草叶长度等),随着越来越多的数据积累,值的分布可能会逐渐类似于以下所示的形状。
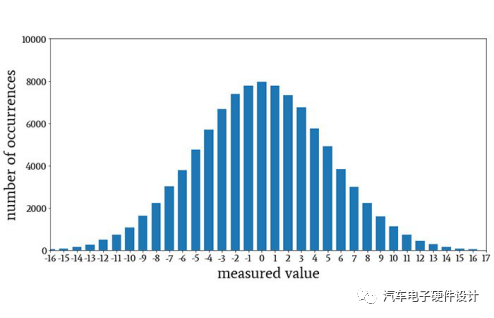
表示正态分布或高斯分布的直方图。
这称为正态分布或高斯分布。它遵循熟悉的钟形曲线形状,但是使用名称“正态”或“高斯”而不是“钟形曲线”非常重要,因为其他类型的分布具有相似的形状。在进行统计分析时,在工程,物理科学和社会科学领域研究的大量现象将产生正态分布。
正态分布的特征
正态分布是一种数学上定义的关系,用于描述数据集中的值,而现实生活中的测量值随着样本量的增加而近似于这种关系。让我们看一下正态分布的一些重要特征。
给定正态分布的特定形状完全由均值和标准偏差定义。换句话说,如果您知道正态分布数据集的平均值和标准偏差,则可以绘制直方图的形状。
平均值确定曲线中心的位置,标准偏差确定其表观宽度。在上面显示的分布中,平均值为0,标准偏差为5。
尽管从理论上讲,高斯曲线延伸到正和负无穷大,但是当值在均值之上或之下大于约3个标准偏差时,预期的出现次数将变得非常小。
直方图和概率密度函数
如果我们为遵循正态分布的变量收集了大量数据,则可以将这些数据显示为直方图,并且将具有高斯曲线形状。另一方面,如果我们知道数据的均值和标准差,则可以画出与我们的经验观察值相对应的概率密度函数。
为此,我们使用以下公式:
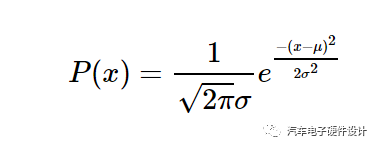
其中,μ是平均值,σ是标准偏差。
这是平均值为0,标准偏差为5的正态分布变量的概率密度函数图。
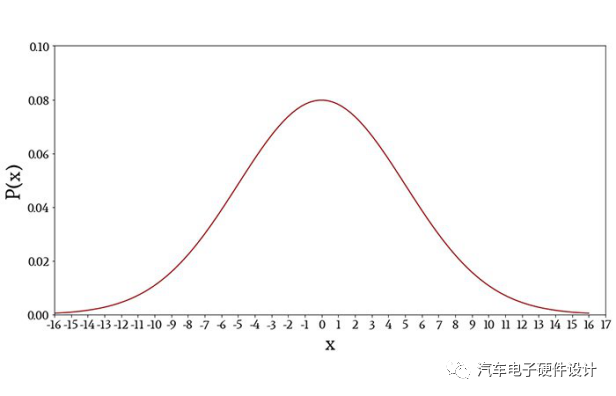
正态分布变量的图密度函数。在这种情况下,平均值为0,标准偏差为5。解释概率密度函数
通过计算给定间隔(例如,从–3到+3)内P(x)曲线下的面积,我们可以确定随机选择的测量值落入该间隔的概率。出于实际目的,我们也可以将P(x)解释为随机选择的测量将近似等于某个值的可能性。
例如,假设上面显示的概率密度函数对应于我们通过测量传感器信号的电压(以毫伏为单位)生成的直方图。所有值均四舍五入至最接近的毫伏。平均值为0 V,标准偏差为5 mV。
我们使用上面给出的公式计算了高斯P(x),并绘制了P(x)来绘制一条曲线,该曲线是所测传感器电压分布的连续数学表示。现在,我们查看该图,发现6 mV的值对应于P(x)= 0.04,这表明随机选择的电压测量值大约为6 mV的可能性为4%。
我发现以这种方式考虑概率密度函数很有帮助,但是请记住,从严格的数学角度来看,这种解释是不正确的。概率密度函数是连续的,因此,概率仅在一个时间间隔内为非零值,而不是沿水平轴的一个精确值。
概率密度函数的归一化
所有概率密度函数都经过归一化,因此曲线下的总面积为1。
这是有道理的:整条曲线下方的区域为我们提供了随机选择的测量值落入与整条曲线相对应的间隔内的可能性。由于该值有100%的机会会在此间隔内某个位置,因此积分P(x)的结果必须为1。
由于这种归一化,如果我们在同一轴上绘制P(x)和直方图,它们将不会重合:P(x)在垂直轴上仅从0扩展到0.08,而直方图从0扩展到8000(因为它是使用100,000个数据点生成的)。
但是,如果我将P(x)乘以100,000,并将结果曲线包括在直方图中,您会发现高斯概率密度函数可以数学方式捕获所测得的分布。
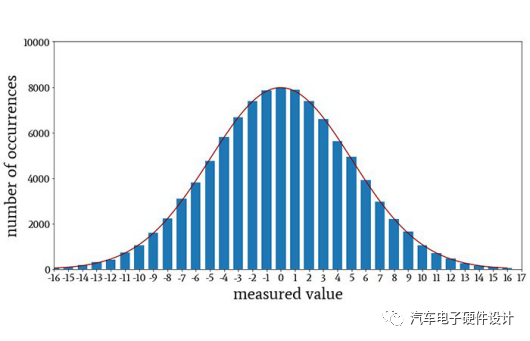
当我们将P(x)乘以100,000并将结果曲线包括在直方图中时,高斯概率密度函数。结论
我希望您喜欢这篇文章,并希望它介绍了正态分布并在实践和理论上取得了很好的平衡。在下一篇文章中,我们将继续讨论正态分布。
责任编辑:lq
-
新编电气工程师手册2025-06-03 354
-
电气工程师手册2009-12-07 11119
-
高级电气工程师??????2016-11-07 5131
-
【下载】电子电气工程师必知必会2017-05-25 73887
-
PLC技术在电气工程及其自动化控制中的应用2021-01-18 2342
-
Visio在电气工程制图中的应用2011-04-01 3172
-
电气工程CAD(图书)2011-06-15 2260
-
计量测试在电气工程中的应用2012-02-13 949
-
电气工程师100条运营知识2016-11-28 2434
-
智能化技术在电气工程自动化控制有怎么样的应用2020-05-27 1538
-
关于正态分布和贝塔分布的案例介绍2020-10-12 8190
-
电气工程师和注册电气工程师的区别2022-10-30 15130
-
电气工程及其自动化2023-04-27 1949
-
mathcad 在电子和电气工程中的应用2023-12-07 3384
-
铜排在电气工程中的应用2025-01-19 2338
全部0条评论

快来发表一下你的评论吧 !

