基尔霍夫电路法详解及应用案例

1845年，德国物理学家古斯塔夫·基希霍夫（Gustav Kirchhoff）制定了一对或一组规则或法律，以处理电路中电流和能量的守恒。这两个规则通常称为：Kirchhoffs电路定律，其中Kirchhoffs定律之一是处理在闭合电路周围流动的电流，即Kirchhoffs电流定律（KCL），而另一条定律是处理闭合电路中存在的电压源，即Kirchhoffs Voltage法律（KVL）。
基尔霍夫斯第一定律–当前法律（KCL）
Kirchhoffs Current Law或KCL指出，“进入结点或节点的总电流或电荷完全等于离开节点的电荷，因为除了离开，它别无其他可去的地方，因为节点内没有电荷损失”。换句话说，进入和离开一个节点的所有电流的代数和必须等于零，I （退出）  + I （进入）  = 0。Kirchhoff的这一观点通常被称为电荷守恒。
基尔霍夫斯现行法律

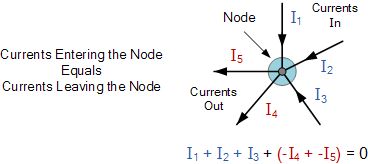
在此，进入节点的三个电流I 1，I 2，I 3均为正值，离开节点的两个电流I 4和I 5均为负值。这意味着我们也可以将等式重写为：
I 1  + I 2  + I 3  – I 4  – I 5  = 0
电路中的节点一词通常是指两个或多个载流路径或元件（例如电缆和组件）的连接或结。同样，为了使电流流入或流出节点，必须存在闭合电路路径。在分析并联电路时，我们可以使用基尔霍夫定律。
基尔霍夫第二定律–电压定律（KVL）
Kirchhoffs电压定律或KVL指出“在任何闭环网络中，环路周围的总电压等于同一环路内所有电压降的总和”，也等于零。换句话说，环路内所有电压的代数和必须等于零。基尔霍夫的这个想法被称为能量守恒。
基尔霍夫电压定律

从环路的任何一点开始，以相同的方向继续，注意所有电压降的方向（正或负），然后返回相同的起点。保持顺时针方向或逆时针方向相同很重要，否则最终电压总和将不等于零。分析串联电路时，可以使用基尔霍夫电压定律。
使用基尔霍夫电路定律分析直流电路或交流电路时，许多定义和术语用于描述所分析电路的各个部分，例如：节点，路径，分支，回路和网格。这些术语在电路分析中经常使用，因此理解它们很重要。
通用直流电路理论术语：
•电路– 电路是一条闭环导电路径，电流在其中流动。
•路径– 连接元素或源的单行。
•节点– 节点是电路中两个或多个电路元件连接或连接在一起的电路的结点，连接点或端子，从而在两个或多个分支之间提供连接点。节点由点表示。
•分支– 分支是连接在两个节点之间的单个或一组组件，例如电阻器或电源。
•回路– 回路是电路中的一条简单闭合路径，其中不会遇到电路元件或节点超过一次。
•网格- 网格是不包含任何其他路径的单个闭环系列路径。网格内没有循环。
注意：
    如果所有组件中流过相同的电流值，则这些组件被称为串联在一起。
    如果组件之间施加相同的电压，则称它们并联连接在一起。
典型的直流电路

基尔霍夫斯电路法例No.1
找出流入40Ω电阻R 3的电流

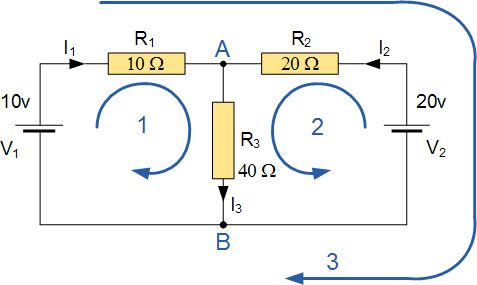
该电路具有3个分支，2个节点（A和B）和2个独立回路。
使用基尔霍夫斯电流定律，KCL的等式为：
在节点A处 ：     I 1  + I 2  = I 3
在节点B处 ：     I 3  = I 1  + I 2
使用基尔霍夫电压定律，KVL方程给出如下：
回路1表示为：     10 = R 1  I 1  + R 3  I 3  = 10I 1  + 40I 3
回路2给出为：     20 = R 2  I 2  + R 3  I 3  = 20I 2  + 40I 3
回路3的公式为：     10 – 20 = 10I 1  – 20I 2
由于I 3是I 1  + I 2的总和，我们可以将等式重写为：
等式 否1：     10 = 10I 1  + 40（I 1  + I 2）= 50I 1  + 40I 2
等式 No     2：20 = 20I 2  + 40（I 1  + I 2）= 40I 1  + 60I 2
现在，我们有两个“联立方程”，可以将其简化为I 1和I 2的值。
换人我1来讲我2给我们带来的价值我1为-0.143安培
换人我2来讲我1给我们的价值我2为0.429安培
如：     I 3  = I 1  + I 2
流经电阻R 3的电流为：     -0.143 + 0.429 = 0.286安培
电阻R 3两端的电压为：     0.286 x 40 = 11.44伏
I 1的负号表示最初选择的电流方向是错误的，但永远不会更有效。实际上，20v电池正在为10v电池充电。
基尔霍夫电路定律的应用
这两个定律使得能够找到电路中的电流和电压，即，称该电路为“已分析”，并且使用基尔霍夫电路定律的基本过程如下：
1.假定所有电压和电阻均已给出。（如果未将其标记为V1，v2，…，R1，R2等）
2.为每个分支或网格分配电流（顺时针或
逆时针）
3.用支路电流标记每个支路。（I1，I2，I3等）
4.找到每个节点的基尔霍夫第一定律方程。
5.为电路的每个独立回路找到基尔霍夫第二定律方程。
6.根据需要使用线性联立方程找到未知电流。
除了使用基尔霍夫电路定律来计算围绕线性电路的各种电压和电流外，我们还可以使用环路分析来计算每个独立环路中的电流，这仅通过使用基尔霍夫定律就可以减少所需的数学运算量。

责任编辑：PSY

原文标题：基尔霍夫电路法分析

文章出处：【微信公众号：multisim】欢迎添加关注！文章转载请注明出处。