

机器人视觉在定位等多个方面发展出来各种方法
描述
机器人视觉是一种处理问题的研究手段。经过长时间的发展,机器人视觉在定位,识别,检测等多个方面发展出来各种方法。其以常见的相机作为工具,以图像作为处理媒介,获取环境信息。
1、相机模型
相机是机器人视觉的主要武器,也是机器人视觉和环境进行通信的媒介。相机的数学模型为小孔模型,其核心在于相似三角形的求解。其中有三个值得关注的地方:
1.1 1/f = 1/a + 1/b
焦距等于物距加上像距。此为成像定理,满足此条件时才能成清晰的像。
1.2 X = x * f/Z
如果连续改变焦距f ,并同时移动相机改变Z,则可以使得物体x在图像上所占像素数目不变(X)。此为DollyZoom原理。如果某个物体在该物体后方(更大的Z),可利用此原理任意调整两个物体在相片上的比例。
1.3 焦距越长,则视场越小,可以将远处的物体拍清晰。同时相片会有更大的景深。
2、消失点
消失点是相片中特有的。此点在相片中不直接存在,在现实中直接不存在。由于射影变换,相片中原本平行的线会有相交的趋势。如果求的平行直线在图像中的交点,则该点对应现实中无穷远出的一点。该点的图像坐标为[X1 X1 1]。此点成为消失点。相机光心与消失点的连线指向消失点在摄像机坐标系中的方向。
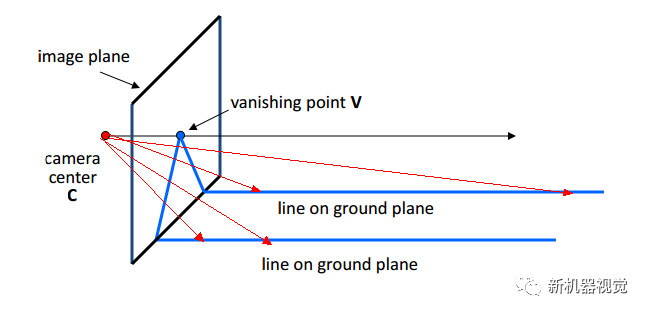
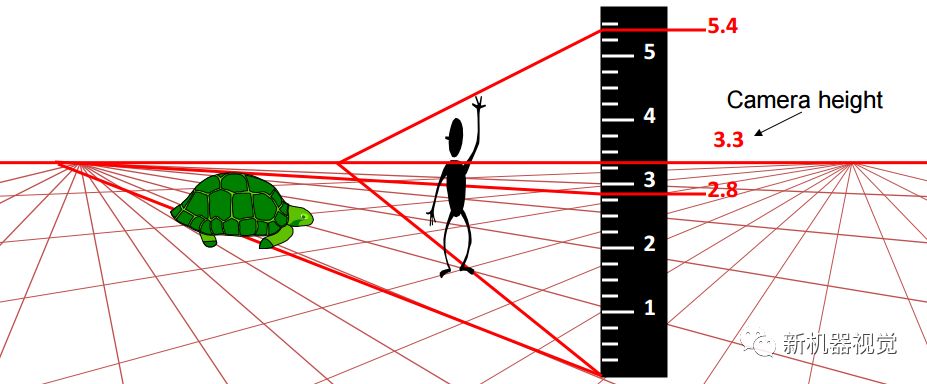
此外,同一平面上各个方向的消失点,会在图像中组成一条直线,称为水平线。该原理可以用于测量站在地上的人的高度。值得注意的是只有相机水平时,horizen的高度才是camera Height.
2.1 位姿估计
如果我们能获得一幅图中的2个消失点。且这2个消失点所对应的方向是相互垂直的(网格),那么我们就可以估计出相机相对于此图像的姿态(靶标位姿估计)。 在获得相机相对于靶标的旋转向量后,如果相机内部参数已知,且已知射影变换矩阵,则可计算相机相对于靶标的距离,那么可以估计机器人的位置。H = K^-1*(H射影矩阵)

2.2 点线对偶
p1×p2 = L12
L12×L23 = p2
3、射影变换
射影变化是空间中平面--->平面的一种变换。对齐次坐标,任意可逆矩阵H均表达了射影变换。简而言之,可以表达为A = HB ,其中AB是[X Y 1]形式的其次坐标。射影变换的一大作用就是将某一形状投射成其他形状。比如,制作相片中的广告牌,或者比赛转播中的广告牌,或者游泳比赛运动员到达后那个biu的一下出现的国旗。射影变换也是增强现实技术的基础。
射影变换的核心在于H的求取。普通的求解方法见机器视觉教材。
假设平面相片的四个点分别是A(0,0,1),B(0,1,1),C(1,1,1),D(1,0,1)。显然,这四个点需要投射到四个我们已知像素位坐标的图像区域中。此外,我们还可以依据像素位置计算两个有趣的点,V1(x1, y1, z1),V2(x2,y2,z2)。这两个点都是图像点。他们对应的实际坐标假设是(0,1,0),(1,0,0)。那么我们就有三个很有趣的实际点了。分别是(1,0,0),(0,1,0),(0,0,1).恰好是一个Identity Matrix。这三个实际坐标经过射影变换会得到像素坐标。像素坐标又是已知的。那么H的第一列就应该对应beta*V2,第二列应该对应alpha*V1。第三列应该对应gama*【A的像素坐标】。alpha beta gama是常数。【射影变化后的坐标应为常数乘以其次坐标】。
如果能解得alpha beta gama,那么我们就获得了射影变换矩阵。显然把C点的像素坐标带入方程,我们则有3个方程,4个未知数(引入了一个lamda)。但是lamda并不影响,除过去后我们只要把alpha/lamda,beta/lamda,gama/lamda当作未知数即可解除射影矩阵。
所以,射影变换矩阵的第一列代表消失点V1,第二列代表消失点V2,第一列与第二列的叉乘,代表水平线方程(点线对偶)。
文章来源:博客园
原文标题:机器人学 —— 机器人视觉(基础)
文章出处:【微信公众号:新机器视觉】欢迎添加关注!文章转载请注明出处。
责任编辑:haq
-
【「具身智能机器人系统」阅读体验】2.具身智能机器人的基础模块2025-01-04 2126
-
机器人视觉技术中图像分割方法有哪些2024-07-04 2153
-
工业机器人视觉装配实训平台实验2021-07-01 1881
-
四元数数控:工业机器人使用机器视觉系统的原因2021-04-29 1329
-
服务机器人的视觉系统怎么设计?2020-04-07 3297
-
机器人的自主决策可靠吗?机器视觉在智能领域占据什么地位?2019-08-16 3280
-
机器人视觉系统组成及定位算法分析2019-06-08 3620
-
LabVIEW 的Tripod 机器人视觉处理和定位研究2019-06-01 2819
-
工业机器人智能发展:视觉和触觉感应简化任务2018-10-26 2525
-
在未知环境中,机器人如何定位、建图与移动?2017-09-21 4870
-
视觉机器人的发展现状与趋势2016-09-08 5229
-
全球机器人发展现状2016-01-28 4049
-
工业机器人经典好书籍——《工业机器人》2015-02-03 31910
-
机器人视觉——机器人的“眼睛”2015-01-23 6158
全部0条评论

快来发表一下你的评论吧 !

