一文汇总4种流行的机器学习算法

本文不仅试图解释算法的工作原理，而且要直观地理解算法的工作原理，以提供这种灯泡啊哈！ 时刻。

决策树

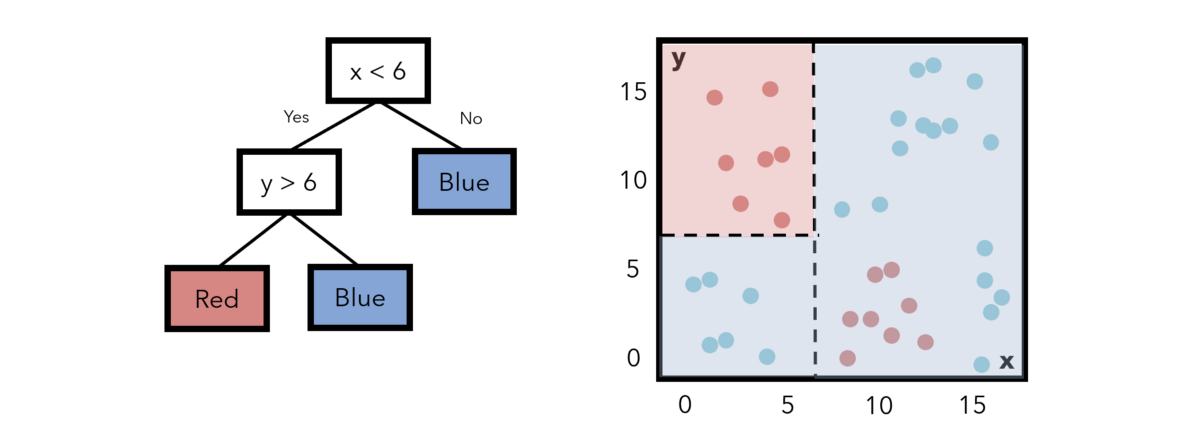
决策树使用水平线和垂直线划分要素空间。 例如，考虑下面一个非常简单的决策树，该决策树具有一个条件节点和两个类节点，指示一个条件以及满足该条件的训练点将属于哪个类别。

请注意，标记为每种颜色的字段与该区域内实际上是该颜色或（大致）熵的数据点之间存在很多重叠。 构造决策树以最小化熵。 在这种情况下，我们可以增加一层复杂性。 如果要添加另一个条件; 如果x小于6，y大于6，我们可以将该区域中的点指定为红色。 此举降低了熵。

在每个步骤中，决策树算法都会尝试找到一种构建树的方法，以使熵最小化。 将熵更正式地看作是某个分隔线（条件）所具有的“混乱”或“混乱”，而与“信息增益”相反的是，分隔线为模型增加了多少信息和洞察力。 具有最高信息增益（以及最低熵）的要素拆分位于顶部。

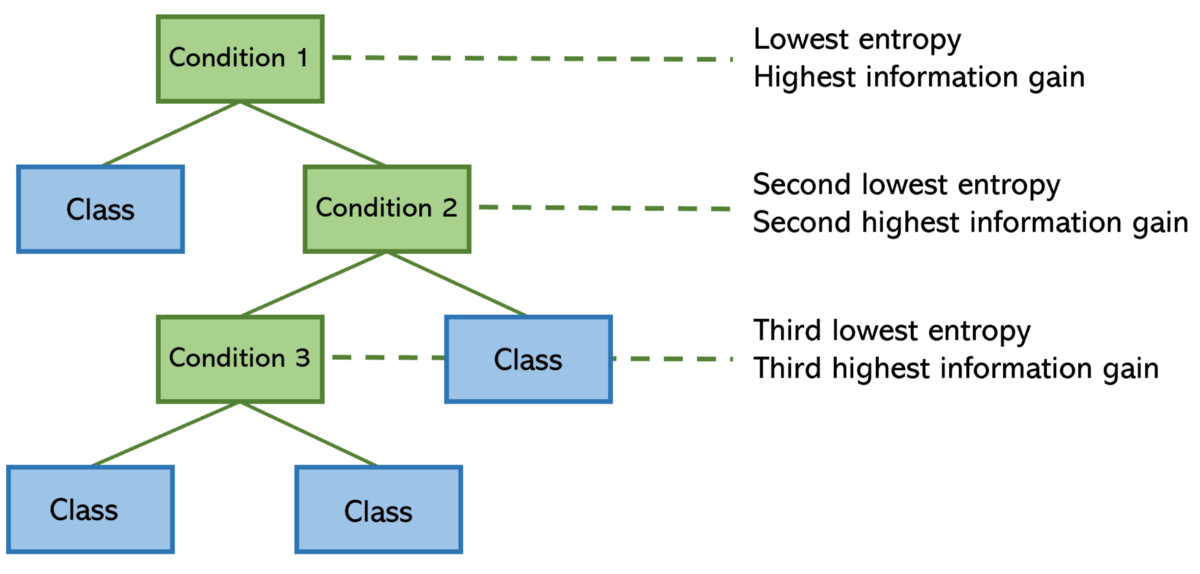
条件可能会将其一维特征分解为如下形式：

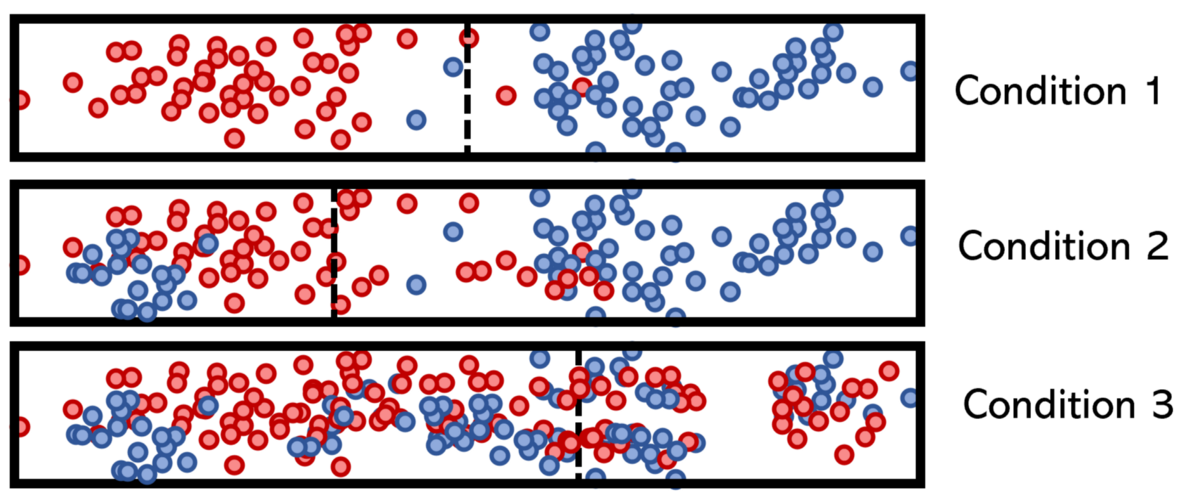
请注意，条件1具有清晰的分隔，因此熵低且信息增益高。 条件3不能说相同，这就是为什么它位于决策树底部附近的原因。 树的这种构造确保其可以保持尽可能轻巧。

您可以在此处阅读有关熵及其在决策树以及神经网络（交叉熵作为损失函数）中的用法的更多信息。

随机森林

随机森林是决策树的袋装（引导聚合）版本。 主要思想是对数个决策树分别训练一个数据子集。 然后，输入通过每个模型，并且它们的输出通过类似平均值的函数进行汇总以产生最终输出。 套袋是组合学习的一种形式。

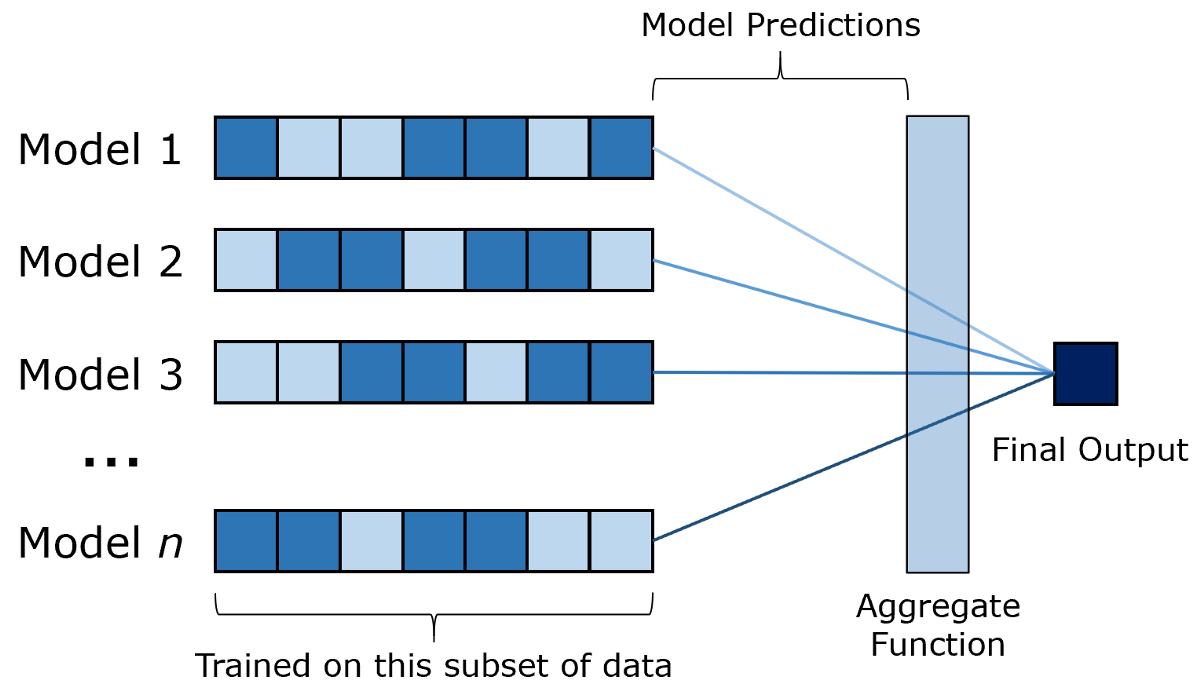
您需要确定下一家餐厅。 要向某人提出建议，您必须回答各种是/否问题，这将使他们做出您应该去哪家餐厅的决定。

您愿意只问一个朋友还是问几个朋友，然后找到方式或普遍共识？

除非您只有一个朋友，否则大多数人都会回答第二个。 该类比提供的见解是，每棵树都有某种“思维多样性”，因为它们是在不同的数据上训练的，因此具有不同的“体验”。

这种类比，干净和简单，从来没有真正让我脱颖而出。 在现实世界中，单朋友选项的经验少于所有朋友，但在机器学习中，决策树和随机森林模型是在相同的数据上训练的，因此也具有相同的体验。 集成模型实际上没有接收任何新信息。 如果我可以向一个全知的朋友提出建议，我不会反对。

在相同数据上训练的模型如何随机抽取数据子集以模拟人为的“多样性”，其效果如何比在整个数据上训练的模型更好？

拍摄正弦波，并带有大量正态分布的噪声。 这是您的单个决策树分类器，它自然是一个高方差模型。

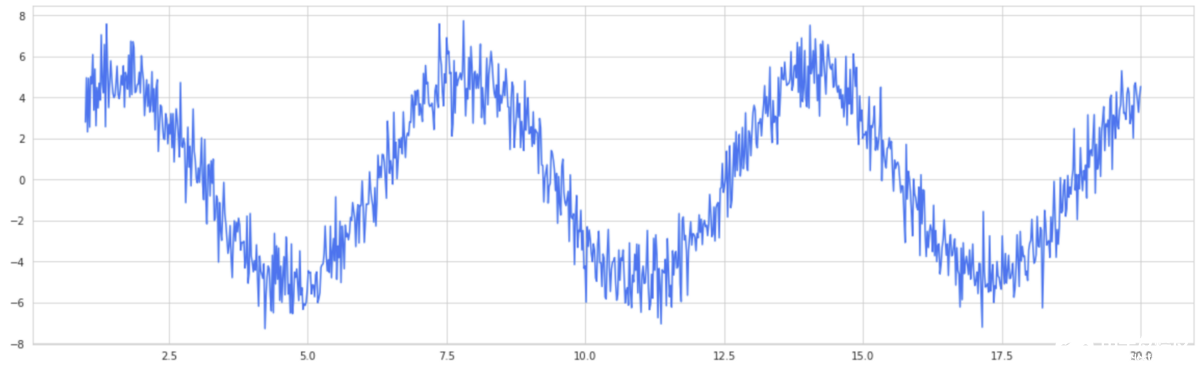
将选择100个“近似值”。 这些逼近器沿正弦波随机选择点并生成正弦曲线拟合，就像在数据子集上训练决策树一样。 然后将这些拟合平均，以形成袋装曲线。 结果？ -更平滑的曲线。

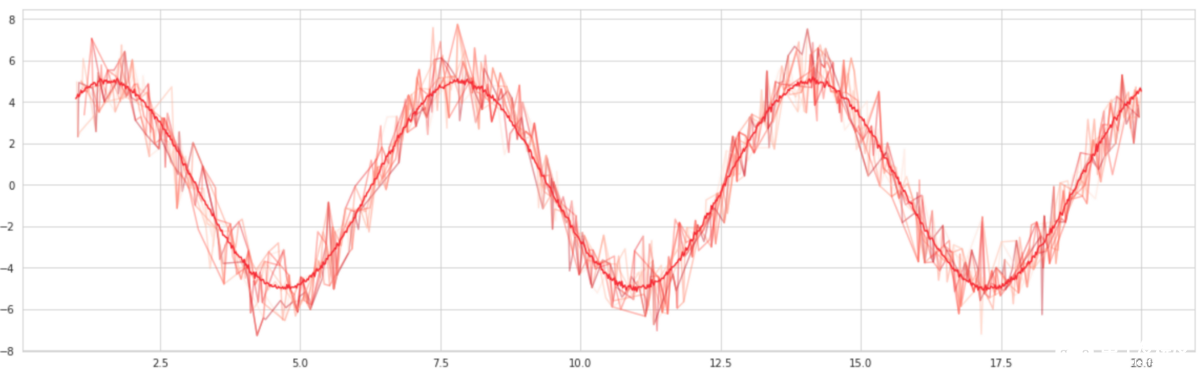
套袋有效的原因在于，它通过人为地使模型更具“信心”，从而减少了模型的差异并有助于提高泛化能力。 这也就是为什么装袋在诸如Logistic回归之类的低方差模型中效果不佳的原因。

您可以在这里阅读更多关于直觉的信息，以及关于套袋成功的更严格的证明。

支持向量机

支持向量机依靠“支持向量”的概念来最大化两个类别之间的距离，试图找到一种可以最好地划分数据的超平面。

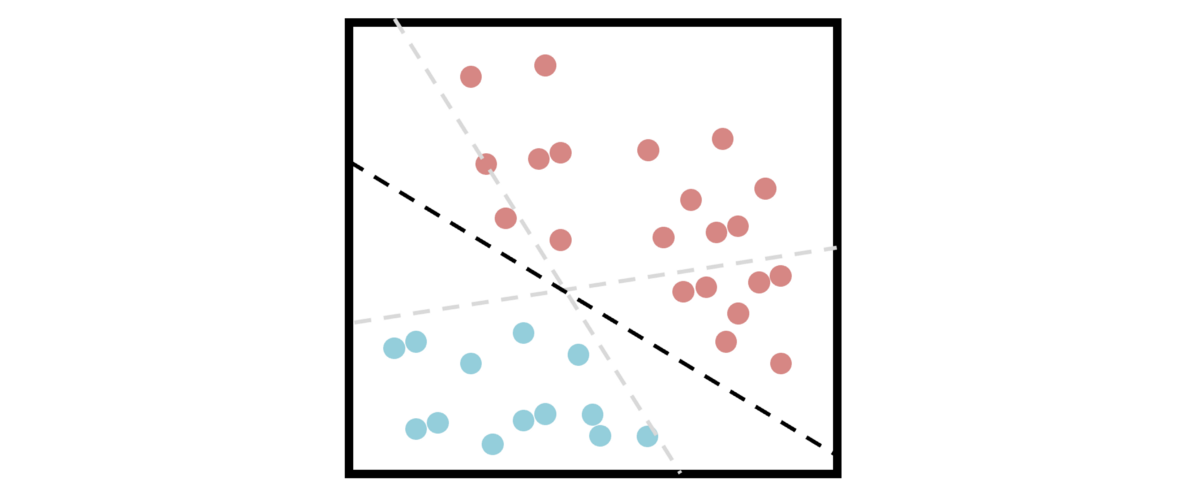
不幸的是，大多数数据集并不是那么容易分离，如果能够分离，SVM可能不是处理它的最佳算法。 考虑此一维分离任务; 没有良好的分隔符，因为任何一种分隔都会导致将两个独立的类归为同一类。

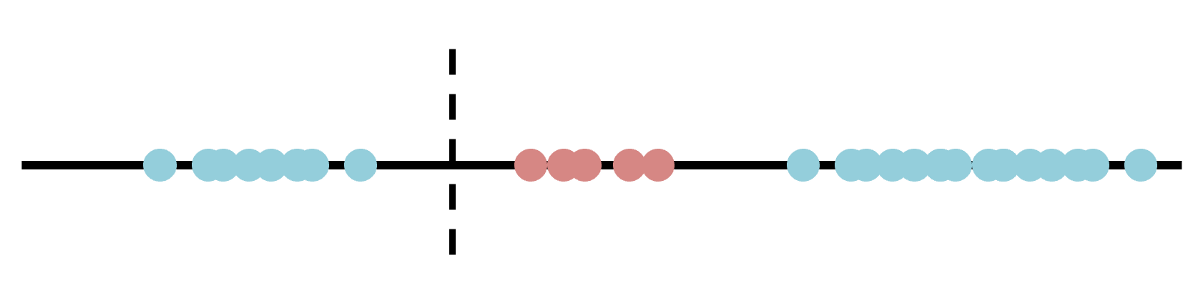
》 One proposal for a split.

SVM通过使用所谓的“内核技巧”来强大地解决此类问题，该技巧将数据投影到新的维度上，从而简化了分离任务。 例如，让我们创建一个新的尺寸，将其简单定义为x²（x是原始尺寸）：

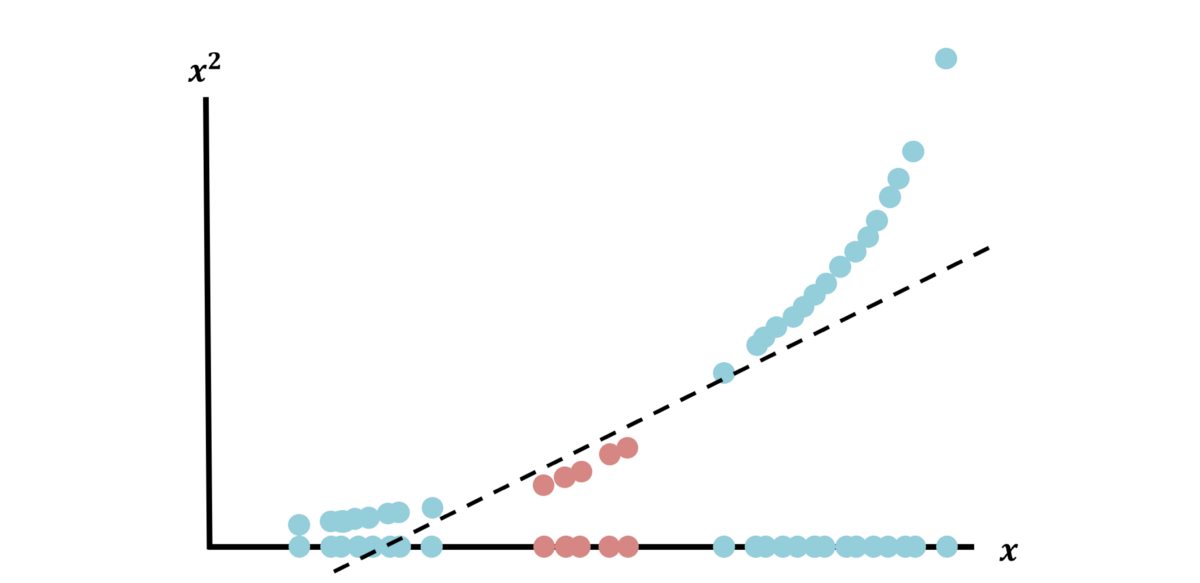
现在，将数据投影到新的维度（每个数据点以两个维度表示为（x，x²））之后，数据就可以清晰地分离了。

使用各种内核（最常见的是多项式，Sigmoid和RBF内核），内核技巧使繁重的工作创造了一个转换后的空间，从而使分离任务变得简单。

神经网络

神经网络是机器学习的顶峰。 他们的发现以及对它的无穷变化和改进使它成为了自己领域的主题，即深度学习。 诚然，神经网络的成功仍然是不完整的（“神经网络是没人能理解的矩阵乘法”），但是最简单的解释方法是通过通用近似定理（UAT）。

每种监督算法的核心都是试图对数据的某些基础功能进行建模。 通常这是一个回归平面或特征边界。 考虑这个函数y =x²，可以用几个水平步长将其建模为任意精度。

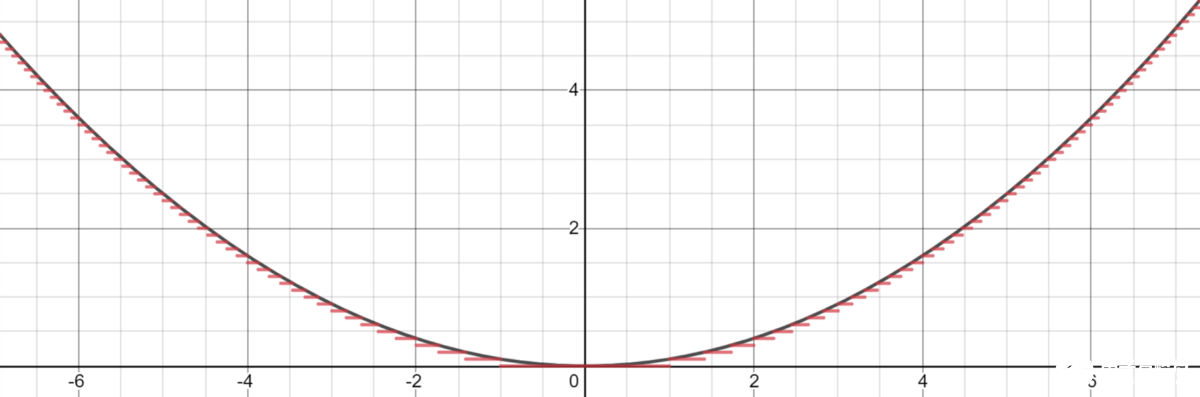
这本质上就是神经网络可以做的。 也许除了水平步长之外，模型关系可能会更复杂一些（例如下面的二次和线性线），但是神经网络的核心是分段函数逼近器。

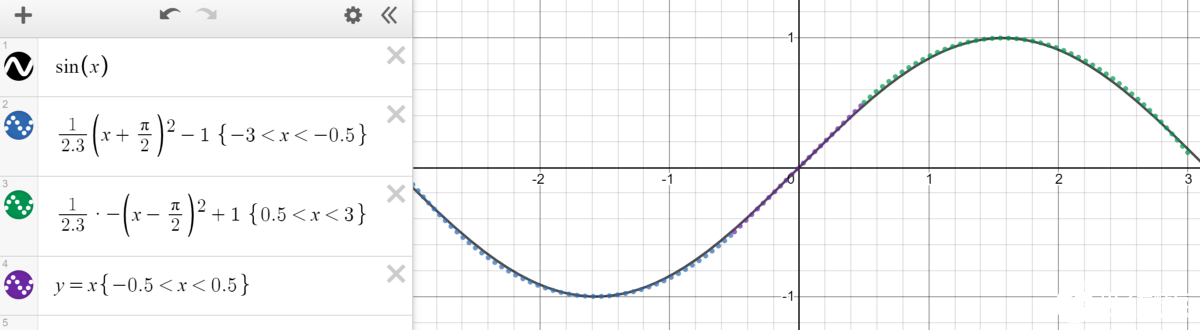
每个节点都委托给分段功能的一部分，网络的目的是激活负责部分特征空间的某些神经元。 例如，如果要对有胡须或没有胡须的男人的图像进行分类，则应将几个节点专门委派给经常出现胡须的像素位置。 在多维空间中的某个位置，这些节点表示一个数值范围。

再次注意，“神经网络为什么起作用”的问题仍然没有得到回答。 UAT并未回答这个问题，但指出在某些人类的解释下，神经网络可以为任何功能建模。 可解释/可解释AI的领域正在涌现，以通过激活最大化和敏感性分析等方法来回答这些问题。

您可以在此处阅读更深入的解释并查看通用近似定理的可视化。

在所有四种算法以及许多其他算法中，这些算法在低维情况下看起来都非常简单。 机器学习的一个关键实现是，我们声称在AI中看到的许多“魔术”和“智能”实际上是一个隐藏在高维伪装下的简单算法。

将区域划分为正方形的决策树很简单，但是将高维空间划分为超立方体的决策树却不那么容易。 SVM执行内核技巧以提高一维到二维的可分离性是可以理解的，但是SVM在数百个大维数据集上执行相同的操作几乎是神奇的。

我们对机器学习的钦佩和困惑是基于我们对高维空间缺乏了解。 学习如何解决高维问题并了解本机空间中的算法，有助于直观理解。
责任编辑人：CC