算法的算法：人工神经网络

在上周的人工神经网络课程中介绍了机器学习中的支持向量机（SVM：Support Vector Machine）与前馈网络RBF的之间的联系，而对于由传递函数为线性函数组成的单层网络的代表自适应线性单元（ADLINE：Adaptive Linear Element）更是和传统信号处理中的自适应滤波器相类似。

这些都会让我们看到神经网络算法似乎能够与很多其他学科算法搭起联系。下面由Matthew P. Burruss的博文中《 Every Machine Learning Algorithm Can Be Represented as a Neural Network》 更是将这个观点进行了详细的梳理。

Every Machine Learning Algorithm Can Be Represented as a Neural Network》：

从1950年代的早期研究开始，机器学习的所有工作似乎都随着神经网络的创建而汇聚起来。从Logistic回归到支持向量机，算法层出不穷，毫不夸张的说，神经网络成为算法的算法，为机器学习的顶峰。它也从最初不断尝试中成为机器学习的通用表达形式。

在这个意义上，它不仅仅简单的是一个算法，而是一个框架和理念，这也为构建神经网络提供了更加广泛的自由空间：比如它包括不同的隐层数量和节点数量、各种形式的激活（传递）函数、优化工具、损失函数、网络类型（卷积、递归等）以及一些专用处理层（各种批处理模式、网络参数随机丢弃：Dropout等）。

由此，可以将神经网络从一个固定算法展拓到一个通用观念，并得到如下有趣的推文：任何机器学习算法，无论是决策树还是k近邻，都可以使用神经网络来表示。

这个概念可以通过下面的一些举例得到验证，同样也可以使用数据进行严格的证明。

1.回归

首先让我们定义什么是神经网络：它是一个由输入层，隐藏层和输出层组成的体系结构，每一层的节点之间都有连接。信息从输入层输入到网络，然后逐层通过隐层传递到输出层。在层之间传递过程中，数据通过线性变换（权重和偏差）和非线性函数（激励函数）变换。存在很多算法来对网络中可变参数进行训练。

Logistic回归简单定义为标准回归，每个输入均具有乘法系数，并添加了附加偏移量（截距），然后经过Signmoid型函数传递。这可以通过没有隐藏层的神经网络来表示， 结果是通过Sigmoid形式的输出神经元的多元回归。

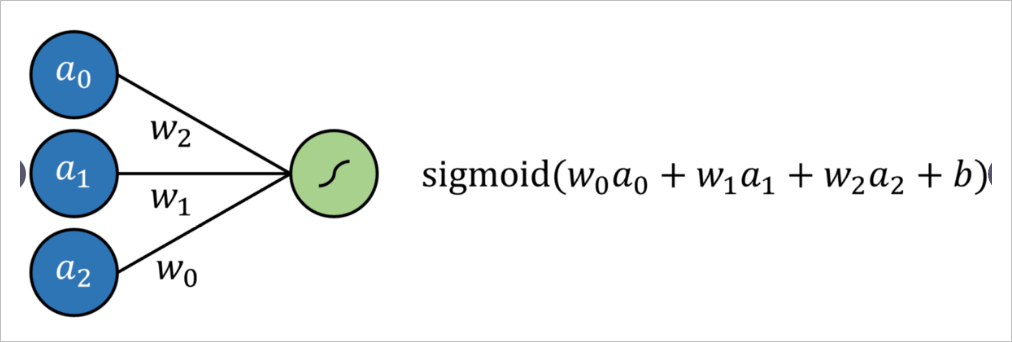
通过将输出神经元激活函数替换为线性激活函数（可以简单地映射输出 ，换句话说，它什么都不做），就形成线性回归。

2.支持向量机

支持向量机（SVM）算法尝试通过所谓的“核函数技术”将数据投影到新的高维空间中，从而提高数据的线性可分离性。转换完数据后，算法可在高位空间获得两类之间最优的分类超平面。超平面被简单地定义为数据维度的线性组合，非常像2维空间中的直线和3维空间中的平面。

从这个意义上讲，人们可以将SVM算法看作是数据到新空间的投影，然后是 多重回归。神经网络的输出可以通过某种有界输出函数传递，以实现概率结果。

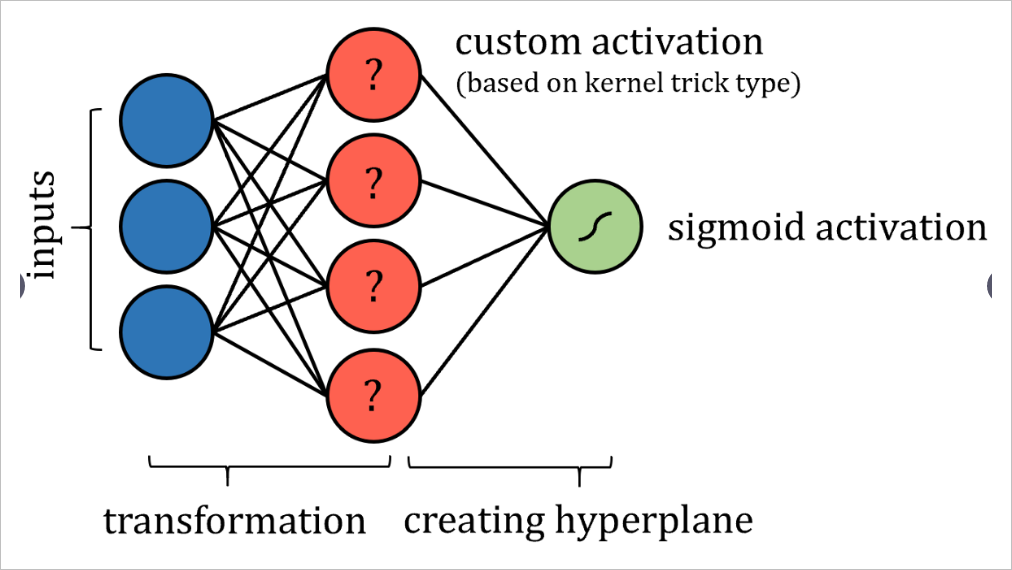
当然，可能需要实施一些限制，例如限制节点之间的连接并固定某些参数，这些更改当然不会脱离“神经网络”标签的完整性。也许需要添加更多的层，以确保支持向量机的这种表现能够达到与实际交易一样的效果。

3.决策树

诸如决策树算法之类的基于树的算法有些棘手。关于如何构建这种神经网络的答案在于分析它如何划分其特征空间。当训练点遍历一系列拆分节点时，特征空间将拆分为多个超立方体。在二维示例中，垂直线和水平线创建了正方形。

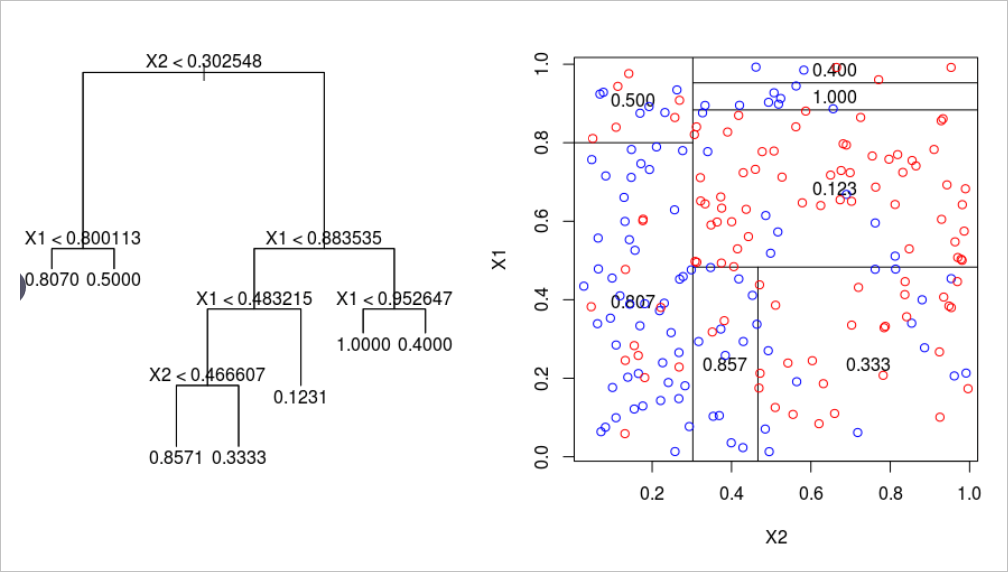
因此，可以通过更严格的激活来模拟沿特征线分割特征空间的类似方式，例如阶跃函数，其中输入是一个值或另一个值-本质上是分隔线。权重和偏差可能需要实施值限制，因此仅用于通过拉伸，收缩和定位来定向分隔线。为了获得概率结果，可以通过激活函数传递结果。

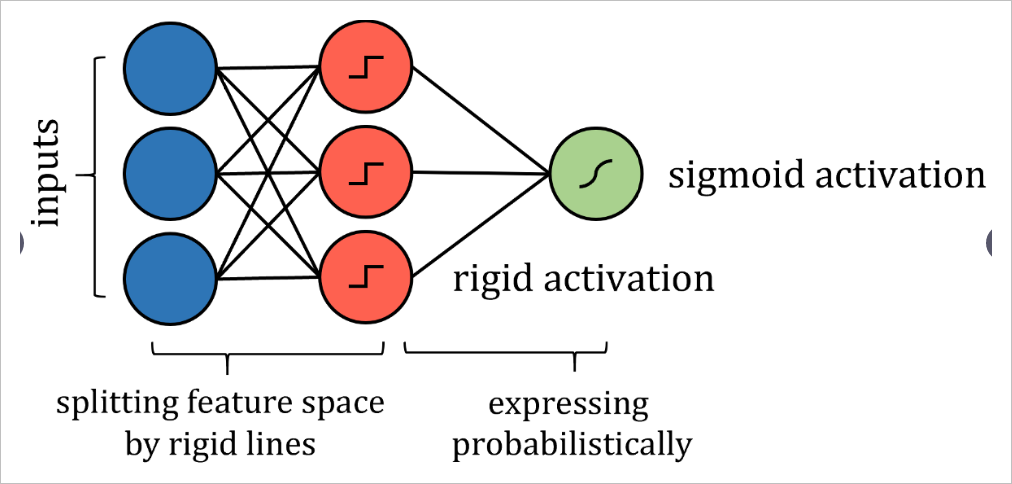
尽管算法的神经网络表示与实际算法之间存在许多技术差异，但重点是网络表达的思想相同，并且可以与实际算法相同的策略和性能来解决问题。

也许您不满意将算法简单地转换为神经网络形式，也许希望看到通用过程可以将所有棘手的算法都进行这种转换，例如k近邻算法或朴素贝叶斯算法等，而不是针对每个算法都手工进行转换。

这种同样算法转换的答案就在于通用函数逼近定理，这也是在大量神经网络工作原理背后的支撑数学原理。它的主要含义是：足够大的神经网络可以以任意精度对任何函数建模。

假设有一些函数 代表数据背后的规律：对于每个数据点 ， 始终返回等于或非常接近 的值。

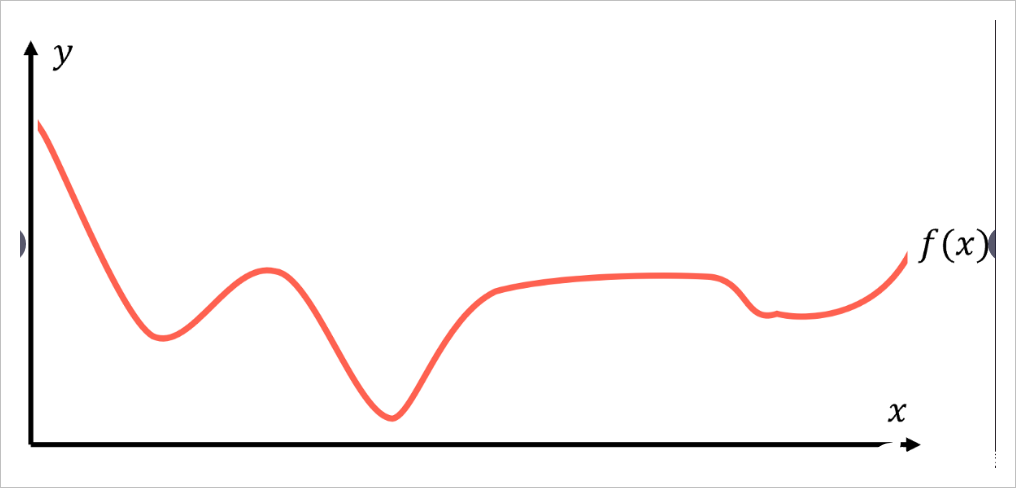
建模的目的是找到该内部映射关系 一个有效表示，我们将其记为预测函数 。所有机器学习算法对这个任务的处理方式都大不相同，采用不同用于验证结果有效的假设条件，并给出具体算法来获得最优结果 。这些获得优化结果p（x）的算法，可说从在这些假设条件限制下，利用纯粹的数学推导获得。描述函数如何将目标映射到输入的函数实际上可以采用任何形式，下面给出几种典型的情况：

有的时候通过数学推导可以对表达式进行求解。但面对大量待定函数参数，往往需要通过不停的试凑来搜索。但是，神经网络在寻找 的方式上有些不同。

任何函数都可以由许多类似阶梯的部分合理地逼近，划分的区间步数越多，逼近的精度就越高。

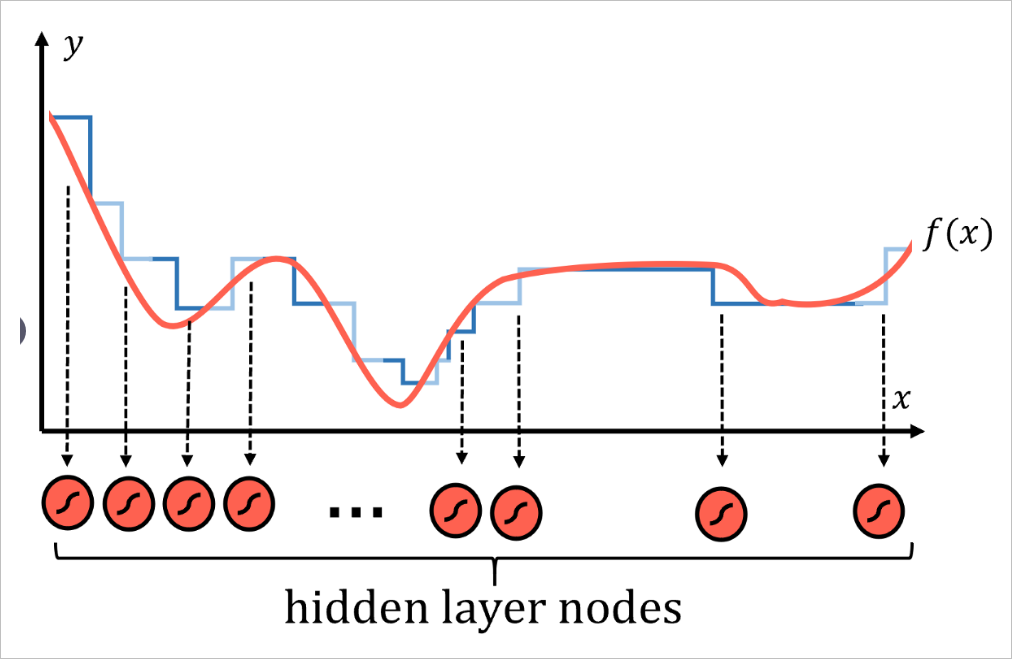
每一个区间都对应神经网络中的一些节点，即隐层中具有S型激活函数的节点。激活函数本质上是概率阶跃函数。实际上每个节点都代表函数 的一个局部。然后，通过系统中的权重和偏差，网络为特定输入来激活不同的神经元，使其输出为1），否则输出0。于是便可以将不同函数的局部最后合并成整个函数。

这种处理模式不仅对应上面的一维函数有效，在图像中也观察到了这种通过激活不同节点以寻找数据中特定的模式。

通用逼近定理已扩展为适用于其他激活函数（如ReLU和神经网络类型），但原理仍然适用。神经网络是实现通用逼近定义的最佳表现形式。

相对于通过复杂方程和关系数学形式来描述通用逼近定理，神经网络则通过构建特殊的网络结构，并通过训练数据来获得结构中的参数。这个过程就好像是通过蛮力记忆将函数存储在网络中。这个汇集众多节点的网络结构，通过训练过程来逼近任意函数过程就表现出具有某种聪明特征的智能系统了。

基于以上假设，神经网络至少可以在理论上构造出一个函数，该函数基本上具有所需的精度（节点数越多，近似值越准确，当然不考虑过拟合的技术性），具有正确结构的神经网络可以对任何其他机器学习预测函数进行建模，反过来，其他任何机器学习算法，都不能这么说。

神经网络使用的方法并不是对一些现有的优化模型，比如多项式回归或者节点系统，只是对少量参数进行优化，它是直接去逼近数据内部所蕴含的规律，而不是基于某种特定的模型来描述数据。这种理念是那些常见到的网络模型结构与其它机器学习之间最为不同之处。

借助神经网络的力量以及对深度学习的不断延伸领域的不断研究，无论是视频，声音，流行病学数据还是两者之间的任何数据，都将能够以前所未有的精度来进行建模。神经网络确实可以被成为算法之算法。

责任编辑：haq