

图深度学习与曾经风靡一时的流形学习有何关系?
描述
如今引领风潮的图深度学习与曾经风靡一时的流形学习有何关系?请看本文娓娓道来。
图神经网络利用关系的归纳偏置获取以图的形式存在的数据。然而,在很多情况下,我们并没有现成的可用的图。
那么,在这种情况下,是否还仍然还可以应用图深度学习呢?在本文中,伦敦帝国理工学院和卢加诺大学的教授Michael Bronstein对近期关于隐图学习的工作和以前的流形学习技术进行了比较。
在过去的几年里,人们对用于图结构数据的机器学习方法的研究兴趣大增。这类数据自然而然地出现在社会科学(例如,Twitter 或 Facebook 上的用户关注图)、化学(分子可以被建模为原子通过化学键相连的图)、生物(不同生物分子之间的交互作用通常被建模为一个被称为「相互作用组」的图)等应用场景下。
图神经网络(GNN)是一类当下非常流行的方法,它们通过共享参数的局部操作对图进行学习,这些操作会在相邻节点之间交换信息。然而,在某些场景下,我们并不能奢求拥有一个作为输入的图。这种情况在许多生物学问题中屡见不鲜,在最好的情况下,由于发现交互作用的实验开销相当大并且充满噪声,「蛋白质-蛋白质」交互网络等图往往也只有部分数据被观测到。
因此,我们对于根据数据推理出图并且将图神经网络应用在该图上十分感兴趣,在本文中,我们将这一过程称为「隐图学习」(latent graph learning)。
隐图可能是面向特定应用的,并且针对下游任务进行了优化。此外,由于这样的图可能会传达关于数据的重要理解并提供解释某些结论的方式,有时它们可能甚至会比任务本身更加重要。我们可以将隐图学习看做学习一个带有空边集的图。
在这种情况下,输入为一些高维特征空间中的点云。
与 PointNet 等针对集合的深度学习方法(它们将一些共享的、可学习的点层面函数应用于每个节点上)不同,我们还试图在点之间传递信息。这是通过在一个根据点特征本身构建的图上传递消息实现的。
本文介绍的第一种此类架构为 MIT 的 Yue Wang 研发的「动态图卷积网络」(DGCNN,这篇论文在计算图形学研究社区十分有名,并常常被用作点云方法的对比基线)。
受到计算图形学领域中进行 3D 点云分析的工作的启发,DGCNN 试图将图用作点云底层的局部平滑流形结构的一种粗糙的表征。
Yue Wang 观察到的一个关键结论是,在整个神经网络的处理过程中,该图并不需要保持不变。而且事实上,顾名思义,「动态图卷积网络」可以、也应该被动态地更新。图 1 说明了 DGCNN 在计算图形学中十分有用的原因:
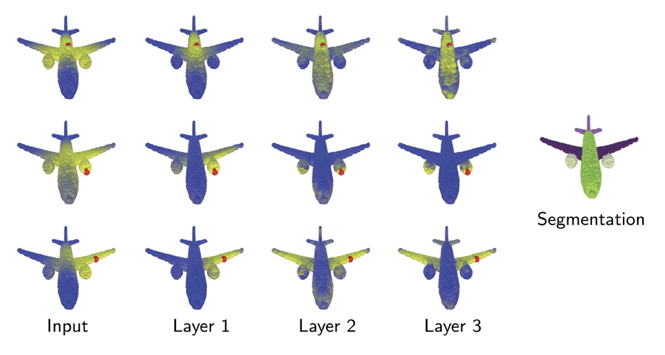
图 1:动态图卷积网络利用飞机图像构建了一个被用于特征传播的 K 最近邻图。这种图依赖于特定的任务,会被每一层网络更新。
图中的不同颜色表明了点距离红点的距离(黄色表示与红点距离较近的点)。
本图说明在分割任务中,较深的层中的图捕获了语义关系(例如,一对翅膀、飞机引擎等)而不是几何关系。
DGCNN 其中的一个不足之处在于,它使用了同一个空间构建图以及图上的特征。如图 2 所示,在慕尼黑工业大学的 Anees Kazi 与 Luca Cosmo 近期发表的工作中,作者提出了一种名为「可微图模块」(DGM)的新型架构,它通过将构建图和构建特征的过程解耦对 DGCNN 进行了扩展:

图 2:可微图模块(DGM)提出了一种构建图及其特征的机制,从而利用输入数据在图上进行信息传播。
在被用于医学领域的问题(例如,根据脑成像数据预测疾病)时,DGM 表现出了非常优异的性能。在这些任务中,我们拥有包括人口统计学特征(例如,年龄、性别等)、脑成像特征在内的多个病人的电子病历数据,并试图预测某个病人是否患有神经系统疾病。
论文「Disease prediction using graph convolutional networks: application to autism spectrum disorder and Alzheimer’s disease 」使用在一个根据人口统计学特征手动构建的「患者图」上的信息传播将 GNN 应用于此类任务。
DGM 在学习图的任务上具有一定优势,它可能传达了对于某些特征如何在特定的诊断任务中互相依赖的理解。除此之外,DGM 还在点云分类任务中稍稍优于 DGCNN。
DGCNN 和 DGM 在概念上与一类被称为「流形学习」或「非线性降维」相似,这类方法在 2000 年代时是机器学习领域中非常流行的课题,并且至今仍然被用于数据可视化。
流形学习的基本假设是:数据有一种内在的低维结构。
如下图所示,尽管我们可以在某个空间中使用数百个甚至数千个维度表征数据,但数据的自由度实际上也许是十分有限的:

图 3:尽管在这个数据集中的手的图像是高维的(64*64=4,096 维),但是他们本质上是低维的,而且可以通过仅仅两个自由度来解释:手腕的旋转和手指的延伸情况。
流形学习算法可以捕获数据集的这种低维的内在结构,并且在欧氏空间中表征它。该图取自论文「A Global Geometric Framework for Nonlinear Dimensionality Reduction」的补充材料。
流形学习旨在通过底层的「流形」(严格地说,这里指的并不是微分几何意义上的术语「流形」,例如不同的点上的局部维度可能不同。
然而,使用这种比喻较为方便。)捕获这些自由度,并且将数据的维度降到其本质的维度上。
流形学习与 PCA 等线性降维方式的重要区别在于,由于数据的非欧结构,用线性投影的方式恢复出流形是不可能的:
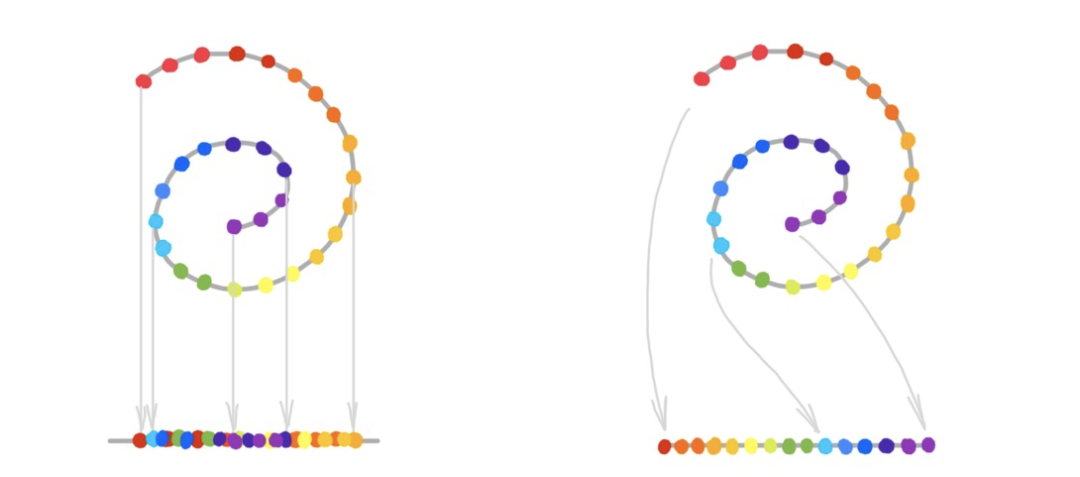
图 4:线性降维(左图)vs 流形学习。Joshua Tenenbaum 创造的「Swiss roll」曲面及其 1D 展开形式在流形学习论文中经常被用作示例。
各种流形学习算法的不同之处在于它们恢复「流形」的方式,但它们的大致框架相同。首先,它们会创建一种数据的表征,通常这是通过构建一个捕获了局部结构的 k 最近邻图完成的。接着,它们会计算一种数据的低维表征(嵌入),并试图保留原始数据的结构。
而这一步正是大多数流形学习方法各不相同的地方。
例如,Isomap试图保留图的测地线距离;局部线性嵌入找到了一种邻接点的局部表征;而拉普拉斯特征映射使用了图拉普拉斯算子的特征函数作为低维嵌入。这种新的表征将原始的非欧结构「展平」到了一个易于处理的欧氏空间中。
最后,一旦我们计算出表征,就可以将某种机器学习算法(通常为聚类算法)应用于该表征上。
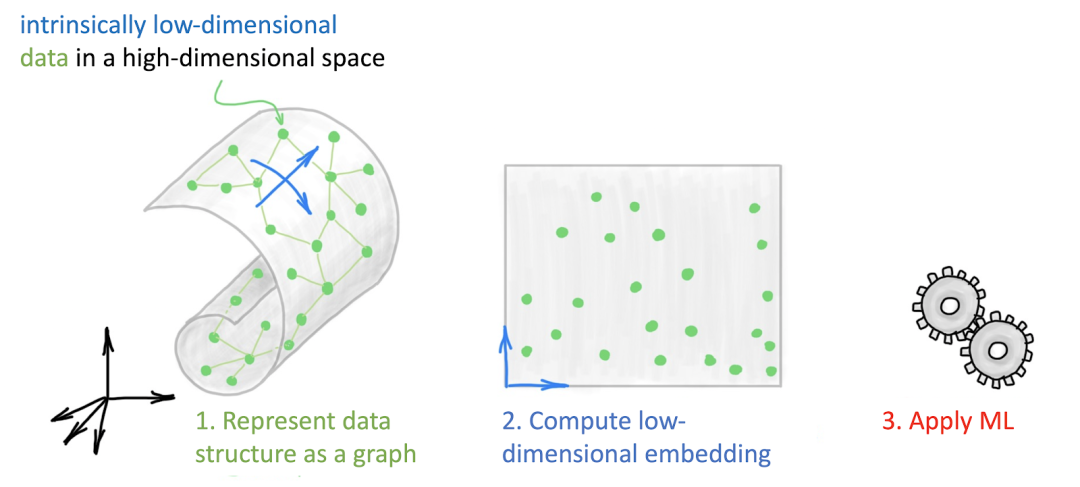
图 5:流形学习方法的框架:首先,将数据表征为一个图。接着,计算出该图的低维嵌入。最后,将某种机器学习算法应用于该低维表征上。
该过程也存在着一些挑战,例如:构建图的过程与应用机器学习算法的过程是解耦的,有时还需要进行精细的参数调优(如近邻节点的数量或邻域半径),从而确定如何构建图,使得下游任务表现优异。
也许,流形学习算法的一个更为严重的缺点是,数据很少表现为低维的原始形式。
例如,当我们处理图像时,需要在预处理步骤中使用各种手动构造的特征提取技术。
图深度学习通过使用一个图神经网络代替这个三阶段的过程为其提供了一种现代化的视角。
例如,在动态图卷积网络或 DGM 中,构建图和学习的过程都是同一个架构中的某一部分:
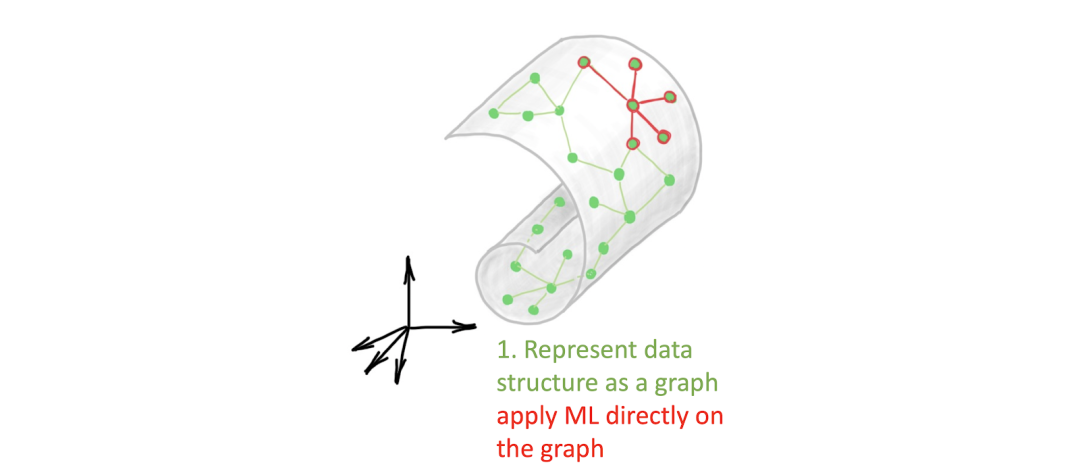
图 6:可以将隐图学习看做一种现代环境下的流形学习问题,其中将图作为一个端到端的 GNN 工作流程的一部分进行学习,并为某些下游任务对其进行优化。
这类方法吸引人的地方在于,它们可以将处理单个数据点的过程与处理它们所在空间的过程在同一个工作流程中结合起来。
以图像为例,我们可以使用传统的卷积神经网络从每张图像中提取视觉特征,并且使用图神经网络建模它们之间的关系。
Jan Svoboda 在论文「 PeerNets: Exploiting peer wisdom against adversarial attacks」中用到了这种方法,他为卷积神经网络提出了一种基于图的正则化层「PeerNet」,它可以实现在多张图像之间交换信息。
PeerNet 与非局部(Non-local)均值滤波器在它们从多个位置聚合信息的方式上有一些相似之处,而 PeerNet 的不同之处在于它从多张图像而不是单张图像中聚合信息。
这种正则化技术显著地降低了对抗性干扰的影响,而标准的卷积神经网络则很容易受其影响。

图 7:PeerNet 是一种标准的卷积神经网络中的基于图的正则化层,它从多张图像中聚合相似的像素,从而降低对于对抗性干扰的敏感度。隐图学习还有许多其它有趣的应用,小样本学习便是其中之一。
在小样本学习中,基于图的技术可以帮助使用少量示例训练的模型泛化。如今,由于数据标注的开销十分巨大,小样本学习在计算机视觉领域变得越来越重要。生物学是隐图学习另一个重要的应用场景,人们通常通过实验观察蛋白质等生物分子的表达水平,并试图重建它们的相互作用和信息传递网络。
此外,隐图学习还可以被用于对物理系统的分析,其中图可以描述多个物体之间的相互作用。具体而言,研究复杂粒子相互作用的高能物理学家们近期对基于图的方法展现出了浓厚的兴趣。最后,隐图学习在自然语言处理(NLP)领域中也得到了重要的应用,其中图神经网络可以被看做 Transformer 架构的拓展。
许多上述的任务也提出了引入图结构的先验知识的问题,这仍然是一个有待解决的开放性问题:例如,我们也许会希望迫使图遵循某些特定的构建规则,或者与某些统计模型兼容。
在论文「Learning deep generative models of graphs」中,作者在严格遵循某些构建规则的情况下,生成化学键的分子结构图。我们相信,尽管隐图学习并不是一个完全新颖的概念,但是它为一些老的问题提供了新的视角。
它肯定是一种有趣的图机器学习问题,为图神经网络的研究者们提供了新的舞台。
责任编辑:lq
-
AI大模型与深度学习的关系2024-10-23 3565
-
神经渲染:图形学与深度学习的完美结合2023-09-23 1755
-
如何DIY风靡一时的四轴无人机?2021-12-20 2221
-
流形学习LLE算法的配套Matlab源码汇总2021-08-25 879
-
流形学习与非负矩阵分解架构综述2021-04-12 855
-
机器学习和深度学习有什么区别?2021-03-12 8911
-
风靡一时的畅销“神机”iPhone 6手机将成为绝版2019-07-18 3042
-
如何刻画数据的本质?流形学习能帮到你2019-04-28 3531
-
详解机器学习算法流形学习2019-02-02 7836
-
深度学习与数据挖掘的关系2018-07-04 2863
-
人工智能、机器学习、深度学习有什么关系?2018-06-08 13042
-
增量流形学习正则优化算法2018-02-27 907
-
揭秘AI、机器学习、深度学习关系2016-09-06 3903
-
有监督流形学习算法SLLESVM 在图像检索中的应用2009-06-10 560
全部0条评论

快来发表一下你的评论吧 !

