浅谈IF 信号的模数转换和I/Q 组件的模数转换

现代数字接收器中定位模数转换器 （ADC） 是一个重要问题，它会严重影响设计选择和实现成本。

在现代数字接收器中定位模数转换器 （ADC） 是一个重要问题，它会严重影响设计选择和实现成本。通过信道传输的信号是通过称为调制的过程应用所需信息内容（消息）的时间的模拟函数。无线信道给信号增加了噪声。它还会产生多路径并导致延迟和信号衰减。接收器必须与它的影响作斗争。信道均衡通常在接收信号转换为基带后在数字域中执行。基带下变频任务通常需要不止一个步骤。模拟信号首先是 下变频为中频 （IF），然后拆分为同相和正交 （I/Q） 分量，然后进行基带移位。在某些电信应用中，IF 采样是通过避免中频转换直接将 I/Q 分量转移到基带的不错选择。然而，在大多数应用中不能应用中频采样，必须使用复杂的外差（模拟或数字，取决于应用）来实现频率转换。必须执行模数转换的位置是接收机设计中的一个关键问题，插入数字信号处理 （DSP） 的最佳点取决于所需的系统性能要求和成本与带宽和信号的匹配噪声比（即 速度和精度）信号处理器和转换器的限制。目前有两种选择：

将 ADC 立即放置在 IF 移位模块之后，其中 I/Q 组件的基带下变频完全在数字域中执行。

在 I/Q 分量转换为基带之后放置 ADC（I/Q 下变频仍然在模拟域中执行，而解码、一些时间恢复任务和信道均衡在数字域中执行）。

第一种方法需要高性能 ADC，这意味着高功耗和增加的设计成本。但它的优点是可以在接收器链中较早地应用数字信号处理，这在一些新应用（即软件定义无线电）中是强烈推荐的。另一方面，第二种方法放宽了对 ADC 的要求，但增加了 I/Q 组件的不平衡（当使用两个 ADC 时）以及时序不匹配（当在乒乓配置中仅使用一个 ADC 时） 。

在本文中，我们描述了在通过模拟外差将复数 I/Q 分量移至基带后对复数 I/Q 分量执行模数转换的方法。特别地，我们描述了数字 I/Q 不平衡校正所需的数字电路——在这种情况下这是必要的——以及 I/Q 组件的时间恢复，当在乒乓配置中使用单个 ADC 时尤其需要。

IF 信号的模数转换

当用于转换中频信号时，如图 1 的数字接收器所示，对 ADC 的要求变得更加严格。实际上，真实 IF 信号比其复杂的 I/Q 基带分量具有更宽（大约两倍）的带宽。根据奈奎斯特定理，采样频率必须至少选择为单边信号带宽 BW 的两倍，才能完全捕获其信息内容。请注意，对于低通信号，信号的单边带宽与其最高频率分量一致。实际上，奈奎斯特定理所描述的最低采样率（fs=2*BW）只是一个理想的极限。对于新手系统设计者来说，这是一个下界和梦想。众所周知，必须选择采样频率以确保频域中有一些自由空间 ΔΔf，用于分配抗混叠滤波器的过渡带宽 （fs=2*BW+Δf）。高采样率和高精度采样时钟是ADC难以获得的特性；它们极大地影响了设计成本。高分辨率、高静态线性度和动态线性度是转换器处理宽带信号需要考虑的其他基本要求。

流水线和 Σ-Δ ADC 是通信系统中最常用的架构。虽然流水线架构具有通过增加转换级数来提高分辨率的优势，但本质上是窄带 ADC 的 sigma-delta 转换器可以完成单通道应用中所需的一些任务（当以极高的速度起诉时）时钟频率）。通常，为了使噪声整形有效，转换器过采样率必须为 16 或更高。尽管需要高采样率，但 delta-sigma 转换器具有一些适用于通信应用的有用功能。例如，可以设计具有非对称信号传递函数的复杂带通 delta-sigma，为低中频信号提供额外的镜像抑制。

为了使用较低的采样频率，对于接收信号具有稀疏或带通性质的某些特定电信应用（例如，蜂窝基站），通常的做法是以较小的速率对中频信号进行采样其最大频率的两倍（IF 采样或低速率采样）。当应用于 IF 信号时，以低速率采样方式，单个 ADC 将实际信号数字化，然后使用数字信号处理方法将其转换为数字域中的复杂分量。这种技术的优点包括降低硬件复杂性、工作量、功耗和成本。这些优势是可能的，因为 IF 采样方法会自动执行部分下变频任务。

尽管 IF 采样技术提供了许多好处，但一个重要的缺点是噪声混叠。如果输入信号的频带限制不够，这种混叠会降低等效 ADC SNR 性能，从而允许混叠频带中的噪声与所需信号一起被数字化并转换为基带。此外，在应用中频采样时，系统需要配备过渡带相对较窄的带通抗混叠滤波器。窄过渡带意味着高品质因数 Q 以及高滤波器阶数。因此，IF 采样只能用于某些特定应用。例如，当接收频谱中存在相邻干扰信号时（即输入信号不具有稀疏性），中频采样就不是一个可行的选择；相当，

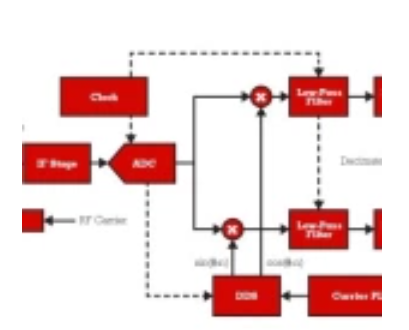
与其讨论需要高性能 ADC 的中频信号采样的可能性，或探索使用低速率采样的可能性，我们将重点关注执行低通采样 （fs=2*BW+？f） 的选择通过一对模拟混频器将复杂的 I/Q 信号分量移至基带。在接下来的部分中，我们提出了两种执行 I/Q 采样的方法，讨论了它们各自隐含的缺点，并提供了数字补偿电路来纠正它们对采样数据信号的负面影响。

I/Q 组件的模数转换

在将 I/Q 分量转移到基带之后对其进行数字化是当今通信接收器中最常用的解决方案。这种方法的优点是放宽了 ADC 要求，因为基带组件的带宽大约是相应真实 IF 信号带宽的一半。

I/Q 分量的采样可以通过两种方式实现：

一对匹配的（几乎）ADC。

具有乒乓配置的单个 ADC。

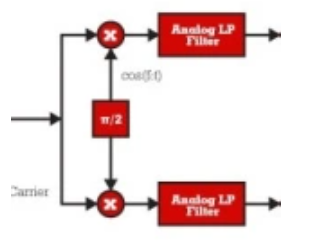
具有两个转换器的解决方案（其框图如图 2 所示）放宽了 ADC 要求，但有助于增加 I/Q 不平衡，这主要是由将信号移至基带的一对模拟匹配混频器引入的。

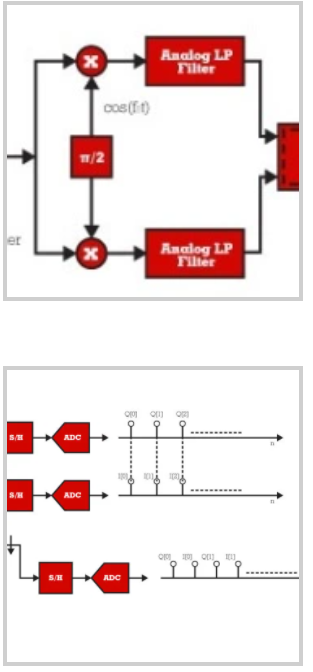
如图 3 所示，采用乒乓配置的一个转换器的解决方案不会增加 I/Q 不平衡。然而，它需要一个数字时间恢复电路来补偿由 I 和 Q 分量之间的乒乓引起的定时偏移。在此配置中，“乒乓”S/H 级与通用 ADC 输入相邻。乒乓级作为两个 S/H 模块运行，每个模块对同相和正交输入通道进行采样。然后将来自两个通道的采样数据多路复用为单个模拟数据流，并由工作在 fs‘=2*fs 的单个 ADC 进行量化，其中 fs 是 I 和 Q 输入采样的频率。然后，解复用器获取 ADC 输出样本，并使它们在 I 和 Q 数字输出总线上可用。乒乓 S/H 级可以设置为单通道操作，在这种情况下，同一 ADC 可用于以全 fs 采样率对 IF 信号进行数字化，或用于以 ADC 采样率 fs 操作的多通道=M*fs 其中 M 是通道数。由于使用了单个 ADC，因此该解决方案非常紧凑。

请注意，在标准配置中，两个 ADC 用于同时采样同相和正交分量。并且由于采样同时发生在 I/Q 路径上，因此从两个组件导出的样本之间没有时间偏移（有关更多详细信息，请参见图 4）。但是，当在乒乓配置中使用单个 ADC 时，I/Q 组件的采样不会同时发生。事实上，I/Q 分量是按顺序采样的。因此，代表两个分量之一的样本导致半个采样周期偏移，这使得在系统中包含同步电路是必要的。由于影响 I/Q 分量的不平衡是影响信号重建的麻烦来源，

在本文的最新部分，我们还提供了在乒乓配置中使用单个转换器时用于数字时间补偿的带通、1 对 2 内插器的架构方案。

数字 I/Q 平衡

调制解调器中模拟正交混频器的增益和相位失配会导致上变频或下变频信号的正负频率分量发生不希望有的耦合。众所周知，这种耦合是一种干扰，会影响通信路径的性能。造成不平衡的最大因素是一对（几乎）匹配的平衡混频器。但是，两条路径中的所有模拟组件（例如滤波器和模数转换器）都会导致失配。在模拟单边带电话系统的时代，与不平衡相关的干扰被视为用户语音通道中令人讨厌的第二音频信号。在当今的调制方案中，干扰限制了通信系统的星座密度。

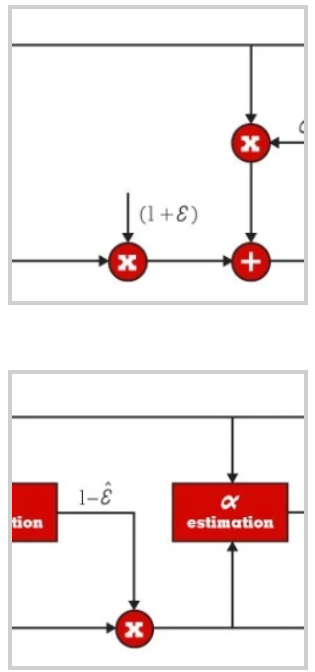
在处理宽带信号的接收器中，控制失配变得更加重要。图 5 显示了 I/Q 下变频器的增益和相位不平衡模型。虽然在两条路径之间分割增益和相位误差项是常见的做法，但我们发现这对增强对问题的理解几乎没有作用。所以我们选择仅将误差分配给两个臂之一。

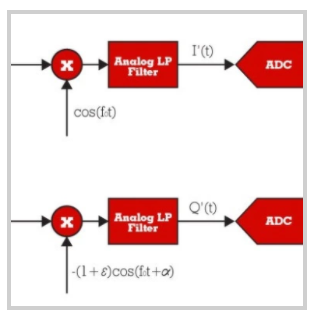
图 6 显示了信号模型，说明了失配对观察到的时域信号的影响。观察到的正交项 I’ 和 Q‘ 通过等式 （1） 中所示的关系与所需的正交项 I 和 Q 相关。此外，等式 （2） 中显示的是这种关系的近似倒数，它根据观察项计算所需项。

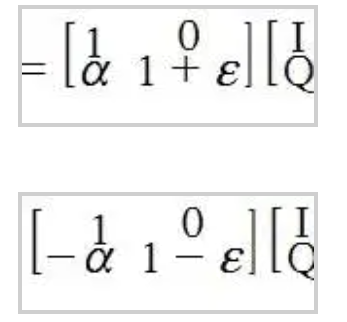
等式 （2） 中的近似倒数反映了由图 7 所示的 I/Q 数字平衡系统执行的信号处理任务。和 ？可以用 1-tap 梯度滤波器递归实现。

数字时间恢复

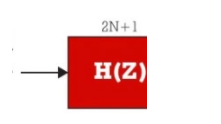
在乒乓配置中使用时，模数转换阶段需要跟随一个必须应用于采样数据流的数字定时恢复阶段，从而导致半个采样周期的偏移。这种情况下的时序恢复电路很容易通过使用基于数字半带滤波器的低成本 1 比 2 多速率插值架构来实现。图 8 显示了基于零插入以提高输入采样率的 1 对 2 上采样过程的初始形式。

然后可以将半带滤波器 H（Z） 划分为一对多相滤波器，如等式 （3） 和 （4） 以及图 9 所示。

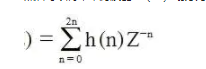
重采样和滤波的顺序可以颠倒，形成图 10 所示的形式。 最后，如图 11 所示，一对 l-to-2 上采样开关和采样延迟可以用两个-tap 换向器执行等效的路径输出调度到输出样本流。

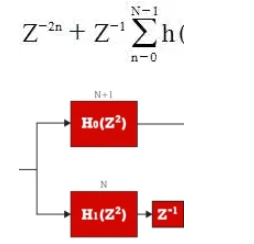
图 11 表示为所需的时间恢复任务选择的 1 比 2 带通内插器的架构。请注意，原型滤波器设计有 2N+1 个抽头，然后分成两条路径，其中一条路径包含零值抽头，并作为仅延迟路径实现，另一条路径包含剩余的 N 个非零抽头。滤波器需要 N 个算术运算 （ops） 来生成两个输出样本以响应每个输入样本。当我们在两个输出上分配每个输入的 N 个操作时，我们发现过滤器工作负载是每个输出 N/2 个操作。通过利用较低路径滤波器中系数集的偶对称性，可以将每个输出的乘法次数减少 2 倍。为了完整起见，我们在此报告图 11 中所示滤波器的长度可以估计为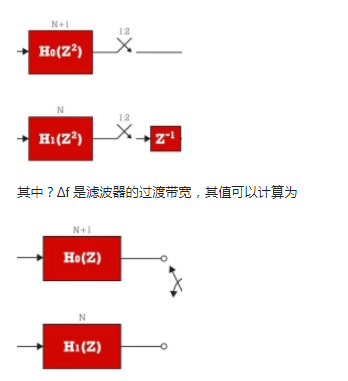

哪里α？是滤波器的过渡带宽。请注意，从等式 （5） 和 （6） 可知，随着滤波器的分数带宽增加，导致过渡带宽减小，滤波器长度增加。

在 1-to-2 内插阶段之后，完成时间恢复的唯一剩余任务是对信号进行下采样，2-to-1，以丢弃位于错误时间位置的样本。请注意，我们将要丢弃的样本是图 11 中 1 到 2 内插器的上路径输出的样本。 因为计算样本没有意义，稍后将在 2:1 下采样中丢弃这些样本在此过程中，信号内插和信号抽取可以通过仅通过由原型半带滤波器的非零抽头组成的下内插器路径处理输入信号来合并。

参考

fj harris，“通信系统的多速率信号处理”，Prentice Hall，Upper Saddle River，新泽西州 07458，2004 年。

F。harris 和 W. Lowdermilk，“软件定义无线电：教程”，IEEE 仪器和测量杂志，2010 年 2 月。

C. Dick， B. Eggs 和 f. harris，“窄带波形的 FPGA 实现时序同步电路的架构和仿真”，SDR 论坛，2006 年，第 1-6 页。

Fredric J. Harris 和 Michael Rice，“用于软件定义无线电中符号定时同步的多速率数字滤波器”，IEEE 通信选定领域杂志，卷。19，没有。12，第 2346-2357 页，2001 年 12 月。

Rice， M.， Dick， C.， & Harris， F. （2001）。“基于 FPGA 的软件定义无线电中的最大似然载波相位同步”。doi:10.1109/ICASSP.2001.941058。

FM Gardner，“数字调制解调器中的插值，第一部分：基础”，IEEE 通信交易，第 41 卷，第 3 期，第 501-507 页，1993 年 3 月。

编辑：hfy