DCM反激转换器在DCM或CCM中的运行方案

DCM操作的特征在于，在下一个开关周期开始之前，转换器的整流器电流降至零。在切换之前将电流减小到零将减少场效应晶体管（FET）的耗散并减少整流器损耗，并且通常还会降低变压器的尺寸要求。

相比之下，CCM操作将在开关周期结束时保持整流器电流导通。CCM操作最适合中功率到高功率应用，但是如果您有可以使用DCM反激式的低功率应用。

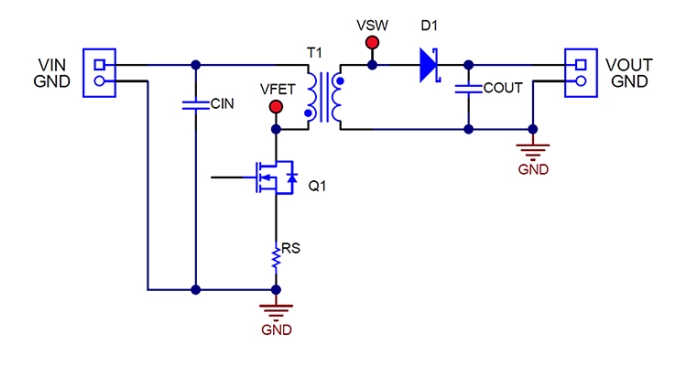
图1：这种简化的反激式转换器可以在DCM或CCM中运行。

图1显示了简化的反激原理图，该原理图可以在DCM或CCM模式下运行。此外，电路可以根据时序在模式之间切换。为了保持本文将要评估的DCM模式下的运行，关键组件开关波形应具有图2所示的特性。

当FET Q1在占空比周期D导通时开始工作。T1初级绕组中的电流始终从零开始，达到由初级绕组电感，输入电压和导通时间t1设定的峰值。在此FET导通期间，由于T1的次级绕组极性，二极管D1被反向偏置，迫使所有输出电流在时间段t1和t3期间由输出电容器COUT提供。

当在1-D期间Q1关断时，T1的次级电压极性反转，这使D1可以将电流传导至负载并为COUT充电。在时间t2内，D1中的电流从其峰值线性减小到零。一旦T1的存储能量耗尽，在t3的剩余时间段内仅会发生残留振铃。这种振铃主要是由于T1的励磁电感以及Q1，D1和T1的寄生电容引起的。在t3期间Q1的漏极电压中很容易看到这一点，该漏极电压从VIN加反射的输出电压降回VIN，因为一旦电流停止流动，T1就无法支持电压。（注：在t3时没有足够的死区时间，可能会发生CCM操作。）CIN和COUT中的电流与Q1和D1中的电流相同，但是没有DC偏移。

图2中的阴影区域A和B突出显示了t1和t2期间变压器的伏微秒乘积，必须保持平衡以防止饱和。区域“ A”代表（Vin / Nps）×t1，而“ B”代表（Vout + Vd）×t2，均参考次级侧。Np / Ns是变压器的初级与次级匝数比。

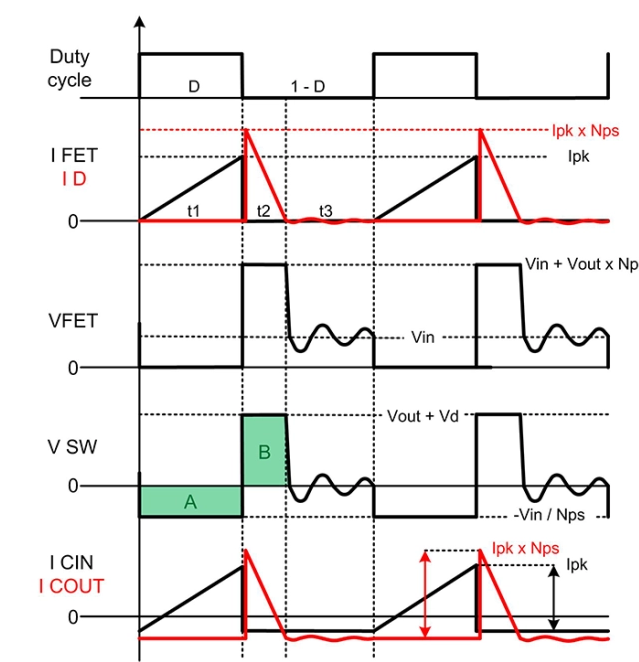
图2 DCM反激式的关键电压和电流开关波形包括设计人员必须指定的几个关键参数。

表1详细列出了相对于CCM的DCM操作特性。DCM的一个关键属性是，较低的初级电感会降低占空比，而与变压器的匝数比无关。此属性使您可以限制设计的最大占空比。如果您尝试使用特定的控制器或保持在特定的开启或关闭时间限制内，那么这可能很重要。较低的电感，这需要较低的平均能量存储（尽管具有较高的峰值FET电流），通常还会导致允许使用比CCM设计所需的变压器更小的变压器。

DCM的另一个优点是，该设计消除了标准整流器中的D1反向恢复损耗，因为在t2结束时电流为零。反向恢复损耗通常表现为Q1功耗的增加，因此消除反向损耗可以减小开关晶体管上的应力。在更高的输出电压下，这样做的好处变得越来越重要，其中，随着额定电压更高的二极管，整流器的反向恢复时间会增加。

表1 DCM反激设计相对于CCM设计既有优点也有缺点。

开发人员在开始设计时将需要了解几个关键参数，以及基本的电气规范。首先选择开关频率（f sw），最大期望工作占空比（D max）和估计的目标效率。然后，公式1在时间t1上计算为：

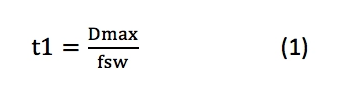
接下来，使用等式2估算变压器的峰值初级电流Ipk。对于等式2中的FET的导通电压（Vds_on）和电流检测电阻器电压（VRS），假定适合您设计的小压降，例如0.5 V。您可以稍后更新这些电压降。

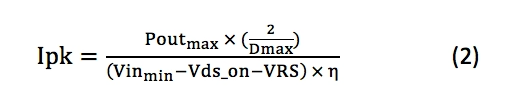
公式3根据图2中的面积A和B计算出所需的变压器匝数比Np / Ns：

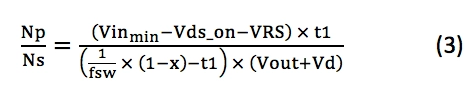
其中，x是t3所需的最小空闲时间（从x = 0.2开始）。

如果要更改Np / Ns，请调整D max并再次进行迭代。

接下来，使用公式4和5计算Q1（Vds_max）和D1（VPIV_max）的最大“平顶”电压：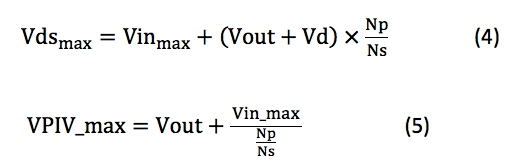

由于这些元件通常会因变压器漏感而产生振铃，因此，经验法则是期望实际值比公式4和5预测的值高10-30％。如果Vds_max高于预期，则减小D max将降低它，但是VPIV_max将增加。确定哪个组件电压更为关键，并在必要时再次进行迭代。

使用公式6计算t1_max，该值应近似于公式1：

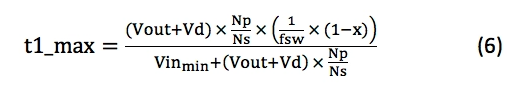
使用公式7计算所需的最大初级电感：

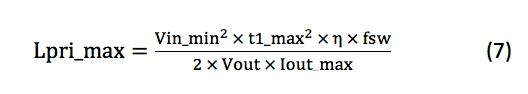
如果选择的电感比公式7所示的电感小，则可通过进行必要的迭代来增大x并减小D max，直到Np / Ns和Lpri_max等于所需值。

您现在可以在公式8中计算D max：

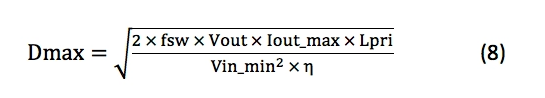
并分别使用公式9和10计算最大Ipk及其最大均方根（RMS）值：

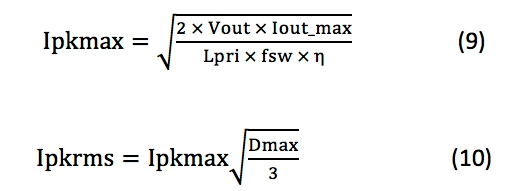
根据所选控制器的电流检测输入最小电流限制阈值Vcs计算允许的最大电流检测电阻值（公式11）：

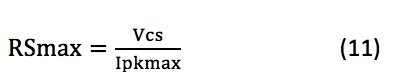
使用公式9和RS中为Ipkmax计算的值来验证公式2中的FET Vds和感测电阻器VRS的假定压降是否接近；如果明显不同，则再次进行迭代。

使用公式12和13从公式10计算RS的最大功耗和Q1的传导损耗：

FET开关损耗通常在Vinmax处最高，因此最好使用公式14计算整个VIN范围内的Q1开关损耗：

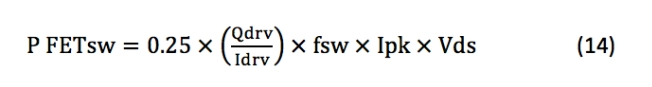
其中Qdrv是FET的总栅极电荷，Idrv是预期的峰值栅极驱动电流。

公式15和16通过FET的非线性Coss电容的充电和放电来计算总功率损耗。公式15中的被积应与0V与其实际工作Vds之间的实际FET的Coss数据手册曲线紧密匹配。在高电压应用中或使用Coss值较大的非常低的RDS（on）FET时，Coss损耗通常最大。

FET总损耗可通过将公式13，公式14和公式16的结果相加得出。

公式17表明，该设计中的二极管损耗将大大简化。确保选择一个额定用于次级峰值电流的二极管，该二极管通常比IOUT大得多。

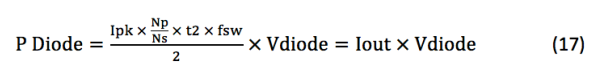
通常选择输出电容作为公式18或19中的较大者，这些公式基于纹波电压和等效串联电阻（公式18）或负载瞬态响应（公式19）计算电容：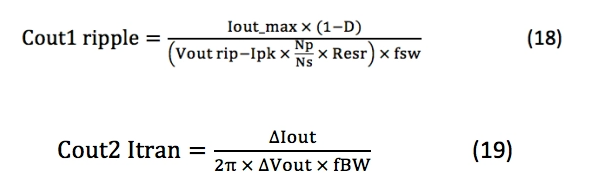

其中∆IOUT是输出负载电流的变化，∆VOUT是允许的输出电压偏移，而fBW是转换器的估计带宽。

公式20计算输出电容器RMS电流为：

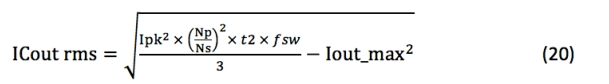
公式21和22估算输入电容器的参数为：

其中VOUT1和Ns1是稳定的输出电压。

变压器初级RMS电流与公式10中的FET RMS电流相同；变压器次级RMS电流如公式27所示。变压器铁芯必须能够处理Ipk而不会饱和。您也应该考虑核心损失，但这超出了本文的范围。

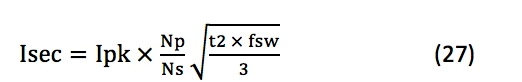
编辑：hfy