如何使用集成电路40106发现未知电容

电压，导体的电阻或通过电线的电流是可以通过使用测试仪容易地测量的量。但是，如果您需要了解一个手工电容器的容量或不读取其板数据的电容器，则需要另一种测量仪器，即“电容表”，它通常很昂贵。有许多方法可以测量任何难度和精度的未知容量值。让我们看看如何借助理论轻松地测量这两个电量。

正弦交流电压下的电容器

当我们向电容器施加直流电压时，如果瞬变消失，则其行为就像开路一样。相反，当电容器处于正弦状态时，它的行为不再像开路那样，而是开始吸收电流，呈现出以欧姆表示的“电容电抗”。该分量类似于电阻。通过使用此原理，我们可以很容易地计算出未知电容器的值，并记住其电抗公式为：

Xc = 1÷2πfC

如果电容器受到正弦周期信号的影响，可以通过一些措施和一些方程式计算出其电容值。

方波电压

电容器方波电容器的行为不同。方波不存在电容电抗。电抗的概念本身取决于正弦信号的存在。由于方波信号是无限正弦波的总和，因此不能显着增加不同频率下正弦波的电抗。因为（理想）电容器是线性的，所以我们可以将方波分解成正弦分量，找到每个分量的相关正弦电压，然后将这些电压相加得出总电压。但是，此测量非常复杂，建议以其他方式更改策略并测量其电容值。

使用的策略

要测量电容器的电容，我们使用一种简单的方法：我们使用由CD40106反相逻辑门和RC网络组成的振荡器生成方波。通过更改C的值（未知），显然可以获得不同的频率。只需对这些值进行“曲线拟合”即可找到一个好的公式，该公式描述了所产生的频率与要显示的电容器的值之间的关系。

电气原理图

这是带有两个电气原理图的两种不同解决方案。第一张图专用于那些具有频率计并可以使用该仪器测量频率的人。它简单得多，几乎不需要电子元件。另一方面，第二个接线图适用于那些没有频率计而是简单的测试仪，甚至是便宜的测试仪的人。因此，该方案与第一种方案相似，但是使用了一个额外的频率/电压转换器来读取普通测试仪上的值。

具有频率计的用户

的第一个接线图第一个接线图更简单，如图1所示。心脏由集成电路CD40106表示，集成电路CD40106与C1和R1一起生成周期性方波信号。频率由C1和R1决定，但是由于R1是固定的，因此它与未知电容器成比例地变化。第一逻辑门（X1）产生信号，第二逻辑门（X2）用作阻抗缓冲器。这样，连接到其输出的任何负载都不会改变所产生信号的频率或幅度。后者在电阻R2上可用，准备使用频率计在频率上进行测量。

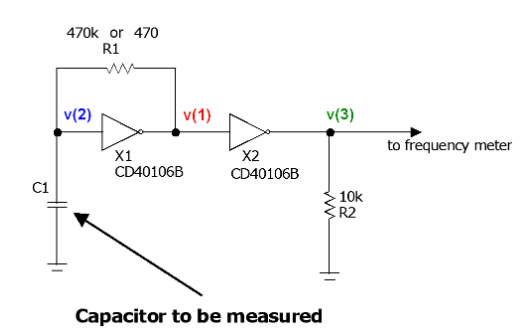
图1：带有频率计的设备的第一个接线图

图2显示了电路上这些点处的信号图：

• 电容器上信号的蓝色曲线图（V2）
• 第一个逆变器输出上的信号的红色曲线图（V1）
• 第二个逆变器输出处的平方信号的绿色曲线图（V3）

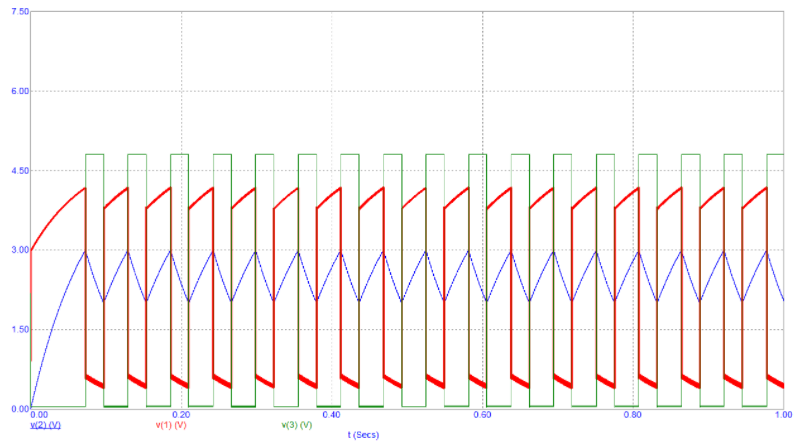
图2：电路各个点的信号图

标度1 pF / 100 nF

下表包含所有理论频率值，这些值仅通过更换电容器C1即可测得。对于此测量范围（介于1 pF和100 nF之间），电阻R1必须为470 k。关系图如图3所示。

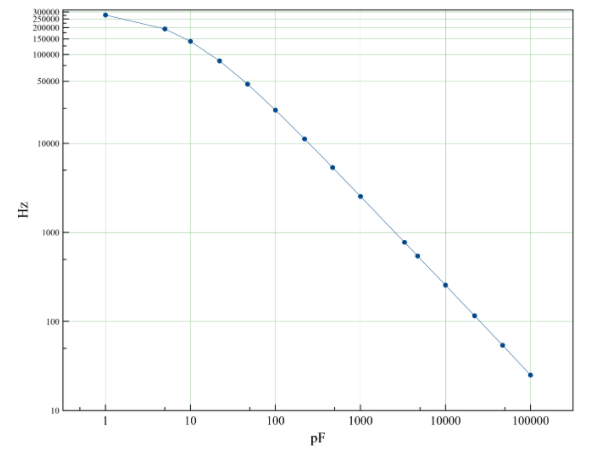
图3：电路电容和频率之间的关系的对数图（R1 = 470 k）

F	赫兹
1个	277,393
5	193,611
10	140,449
22	84,667
47	46,419
100	23,706
220	11,245
470	5,367
1,000（1 nF）	2,542
3,300（3.3 nF）	775
4,700（4.7 nF）	544
10,000（10 nF）	256
22,000（22 nF）	116
47,000（47 nF）	54
100,000（100 nF）	25

对于该值范围，描述电容和频率之间关系的两个公式如图4所示。这是两个非常复杂的公式，它们是从非线性曲线拟合的高级过程中获得的。

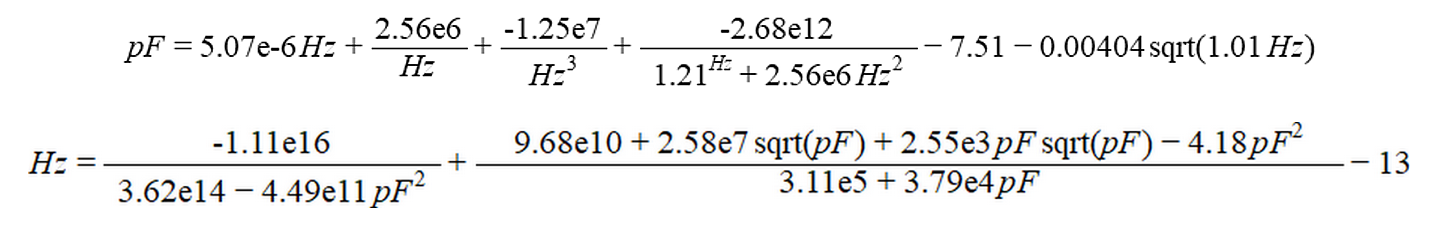
图4：描述两个量之间关系的两个公式

100-nF / 100-µF标度

下表包含替换电容器C1的所有测得的理论频率值。对于此测量范围（介于100 nF和100 µF之间），电阻R1必须为470Ω。关系图如图5所示。

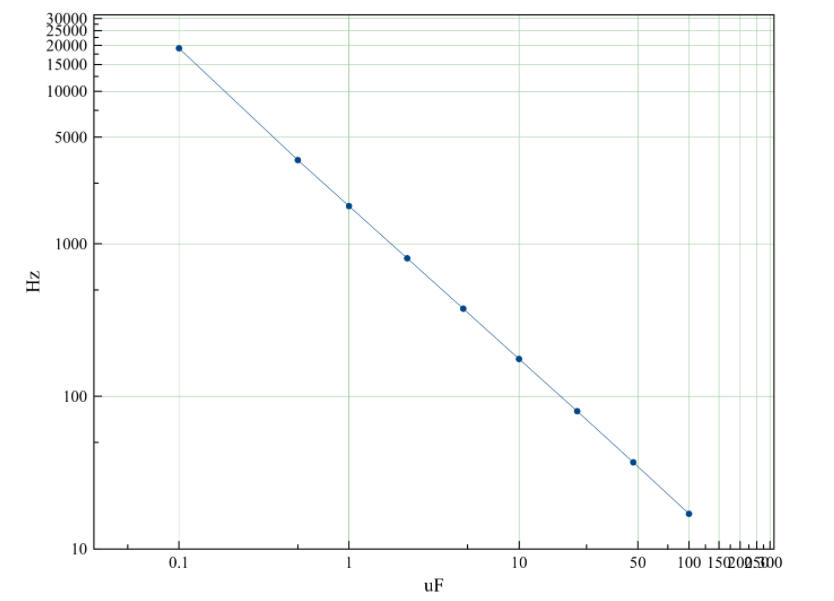
图5：电路电容和频率之间的关系的对数图（R1 = 470Ω）

µF	赫兹
0.1	19,139
0.5	3,540
1个	1,768
2.2	804
4.7	376
10	176
22	80
47	37
100	17

对于该值范围，描述电容和频率之间关系的两个公式如图6所示。

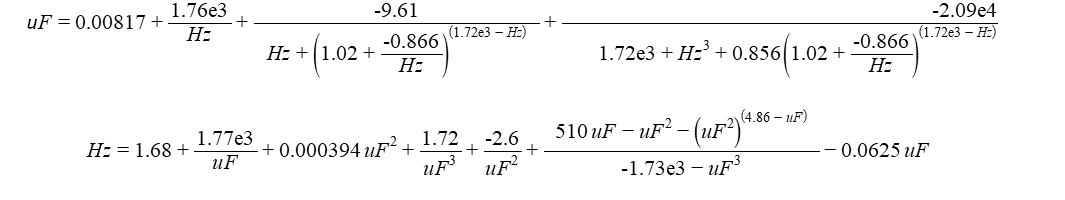
图6：描述两个量之间关系的两个公式

˚F igure 7示出了方波发生器电路和频率米之间的简单布线。对于测量仪器而言，重要的是能够读取周期性方波或矩形波信号的频率。

图7：方波发生器和频率计之间的接线

仅具有测试人员的

用户的第二布线图仅具有测试人员的用户可以实施第二种解决方案。连接到第一个的附加电路将输出频率转换为负电压，可以由通用测试仪测量。与上一个电路相连的新电路是带有“泵”二极管的脉冲重复频率表。整个系统（参见图8）使我们能够根据要测量的电容C1获得负电压。

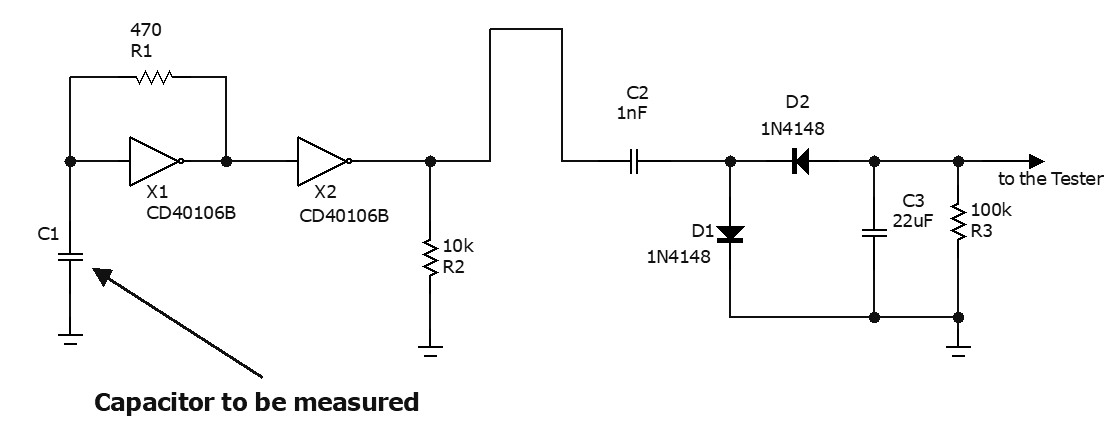
图8：拥有简单测试仪的人员的第二个电路

正脉冲负载在最大电压C2至D1处。在脉冲之间的间隔中，输入为0 V时，C2通过D2快速放电到大电容C3。因此，输出电压与接收脉冲的速度成正比。冷凝器C3类似于一个大罐，被R3慢慢排空。下表包含从不同测量收集的C1电容值不同的数据。该值是指介于100 nF和100 µF之间的电容。为了获得稳定的电压值，必须等待几秒钟的瞬变，如图9所示。

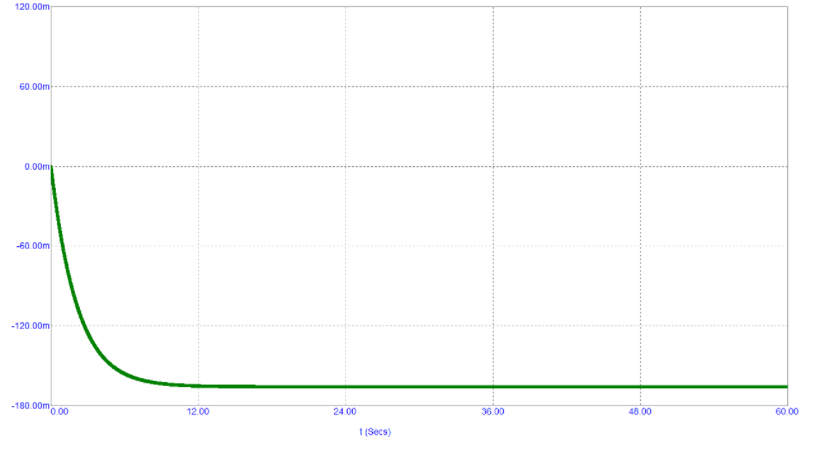
图9：从测量开始几秒钟后获得的稳定电压值。

µF	测试仪R3上的电压（mV）
0.1（100 nF）	–2,655毫伏
0.47（470 nF）	–1,185毫伏
1个	–663.70毫伏
2.2	–334.43毫伏
4.7	–165.62毫伏
10	–80.36毫伏
22	–37.16毫伏
47	–17.48毫伏
100	–8.21毫伏

对于该值范围，描述电容和输出电压之间关系的公式如图10所示。

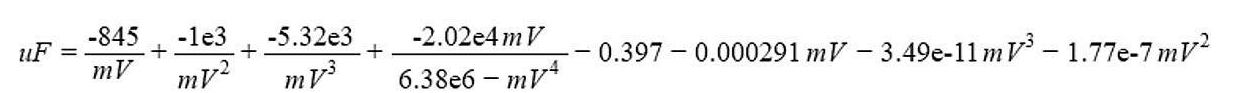
图10：描述两个量之间关系的公式

˚F igure 11示出了方波发生器电路中，频率/电压转换器，并且在VDC模式下配置的正常测试器之间的布线。这是一个非常简单的连接，需要在简单的PCB内构建系统。

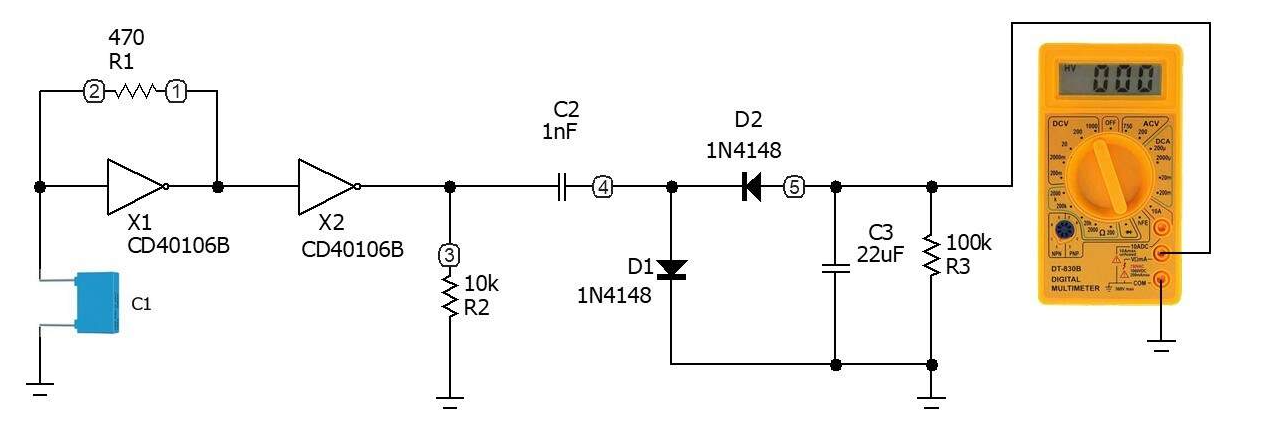
图11：方波发生器，频率/电压转换器和普通测试仪之间的接线

结论

本文中介绍的测量与各种SPICE模型的仿真有关。建议在实际电路上收集数据。用户可以根据所需的电容间隔自由创建自己的数学模型，还取决于瞬态的等待时间和RC时间常数，这可能会产生较长的等待时间。我们建议您尝试根据需要更改电子组件的值。如果在应用公式时遇到困难，则可以简单地查阅收集的数据表，然后通过内插法找到真实的经验数据。为了对数据进行曲线拟合，可以使用任何带有此可用选项的数学和统计软件。本文的主要目的是演示电子与数学是如何紧密联系在一起的。该项目可以针对不同的目的和功能进行任何修改或改进。

编辑：hfy