

一个基本的逐次逼近型 ADC 原理框图解析
描述
这次初步聊一聊 ADC 的相关知识。
BMS 中会用到 ADC,例如集成在单片机内部的,或者独立的;比较有代表性的就是 AFE 中的 ADC,由于 AFE 做了太多的工作,反而弱化了大家对其 ADC 的感知。
在 AFE 中主要存在两种类型的 ADC:即 SAR 型与 Sigma-Delta 型,下面分别介绍。
SAR 型 ADCSAR(Successive approximation register),即逐次逼近型 ADC,例如美信的 MAX17823 使用的就是此类型 ADC。
一个基本的逐次逼近型 ADC 的原理框图如下:由采样保持电路(SHA)、控制逻辑电路、时序发生电路、D/A 转换电路、电压比较电路等组成。
基本原理类似天平称重:如下图所示,假设一个 6bit 的 SAR ADC,则全量程的数字量为 64,为容易理解,假设对应的模拟量也是 64。
那么对模拟量 X=45 进行 AD 转换:首先将 X 与 32 进行比较(0.5 倍 FSR,通过 DAC 设置),因为 X>32,则对应最高 bit 位置为 1;接着 X 与 48 进行比较(0.75 倍 FSR),因为 X<48,则次高位置 0;以此方法继续向下类推,最后得到一个 6 位的二级制代码。即 X=101101,这样就完成了模拟量到数字量的过程。Sigma-Delta 型 ADC 也称作Σ-Δ型 ADC,当然也有人叫做Δ-Σ型 ADC,实际这两种叫法都有人在用,前者可能更贴切;SAR 型 ADC 是直接测量模拟量,而Σ-Δ型 ADC 是属于间接测量模拟量。在 ADI 的 LTC68XX 系列使用的就是此种类型 ADC,内部带有可编程的数字滤波器。
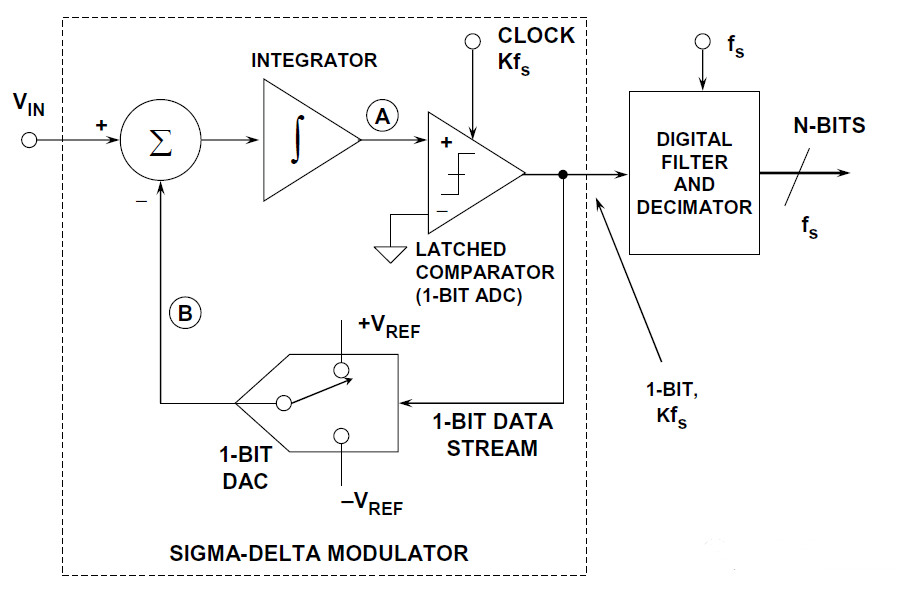
一个典型的Σ-Δ型 ADC 原理框图如下:包括了一个简单的模拟调制电路(积分器、比较器、开关、DAC、求和电路)和一个复杂的数字电路(数字滤波器、数字信号处理器);其中这个模拟调制电路将模拟信号转换为数字 bit 流,而数字电路进一步把数字 bit 流转换为代表模拟输入幅值的数字编码。
Σ-Δ型 ADC 的信号转换流程如下图:把模拟输入电平最终转换成了数字量输出,根据数字量输出大小,可以换算出模拟量的幅值。
进一步地,单独把模拟调制部分拿出来,如下图:
我们仔细看上图,其实整个环路是一个负反馈的闭合回路;由于负反馈的存在,X5 处的电平总是抑制积分器的累加值输出 X3 在 0V 上下波动,这样其实理论上 X5 处的平均值就等于输入信号 X1,时间越长,X5 的平均值越接近 X1;而这种关系其实是映射到了 X4 处输出的 1 的个数。
下面为实际的例子,假设输入 X1 为 0 或 0.5*Vref,波形 A 为积分器输出 X3,波形 B 为比较器输出 X4,就有如下的对应关系:1 的数量越多,代表 X1 越大。
具体计算的话,以上图中的输入 X1=0.5Vref 为例,我们在输出信号 X4 处取 4 个采样点,其中有 3 个 1 和 1 个 0,那么转换为模拟量=3/4*2*Vref-Vref=0.5Vref,与输入 X1 相等。
当你的采样点数量越多,转换出来的值就越准确,所以Σ-Δ型 ADC 就会进行过采样,这也就造成了其转换速度慢的特点。假如输入是一个正弦波,那么此时 X1 与 X4 的对应关系就如下图:同样地,1 的密度大的地方代表 X1 幅值大。
后面的数字电路部分就针对前面得到的 bit 流进行滤波、抽样、处理等操作,最终得到一个 AD 量输出给单片机。
这里再简单提一下Σ-Δ型 ADC 为什么精度高?如下图,左图是普通的 ADC 量化产生的噪声水平,右边是Σ-Δ型 ADC 量化产生的噪声水平,一目了然,Σ-Δ型 ADC 更加优秀;至于怎么推导出来的就比较复杂了,先记住这个结论即可。
总结:
话说查资料时,一定不能只输入 ADC,要不查出来都是英雄联盟相关的内容;ADC 的分类有很多种的,我只挑选了两种有代表性的拿出来学习;以上所有,仅供参考。
编辑:hfy
-
求助,逐次逼近型AD芯片的输入问题2023-12-11 508
-
逐次逼近型ADC:确保有效的首次转换2023-01-30 4819
-
12位逐次逼近型ADC转换的原理是什么2022-02-25 1673
-
请问如何初始化逐次逼近型ADC以实现有效转换?2021-04-07 1276
-
MT-021:ADC架构II:逐次逼近型ADC2021-03-21 1141
-
逐次逼近型ADC的基本原理分析与讲解2019-04-23 15210
-
逐次逼近型 ADC如何确保首次转换有效2018-07-07 3748
-
逐次逼近型ADC的原理2018-03-19 26987
-
如何为逐次逼近型ADC设计可靠的数字接口?2016-01-21 10362
-
为逐次逼近型ADC设计可靠的数字接口2016-01-04 714
-
一种简易实用型电荷加权复用电阻网络逐次逼近型ADC2009-12-18 624
-
什么是逐次逼近型adc2009-05-08 811
-
解析逐次逼近ADC2009-05-04 481
-
理解逐次逼近型ADC2009-04-16 911
全部0条评论

快来发表一下你的评论吧 !

