深度解读正交调制可用于实现无数种调制方案

　　作者：Signal Blue LLC总裁Bob Witte撰文

调制对于电子通信至关重要。调制信号本质上可以是模拟的（语音或音乐）或数字位流。大多数现代通信系统都是数字的，使用离散的幅度或相位电平来表示正在传输的数据。可以可靠地从发送器传输到接收器的独特条件越多，在给定的时间段内可以发送的数据越多。正交调制广泛用于5G及以下的数字通信系统。

调制背后的基本思想是通过调制信号来控制RF载波的一个或多个参数。在数学上，我们可以这样表示：

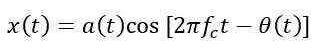
其中：
a（t）是调幅（AM）项
Θ（t）是调相（PM）项
f c 是载频

该信号的幅度由a（t）控制，相位由Θ（t）控制。为了实现幅度调制（AM），我们将调制信号应用为a（t），并将Θ（t）设置为零。类似地，调相（PM）信号将具有设置为常数的（t），并且调制信号将被施加至Θ（t）。现在，我们将忽略频率调制（FM），但将显示可以使用PM创建FM。

矢量表示
矢量表示是通过定义同相（I）和正交（Q）分量来表示调制信号的便捷方法。

使用触发身份：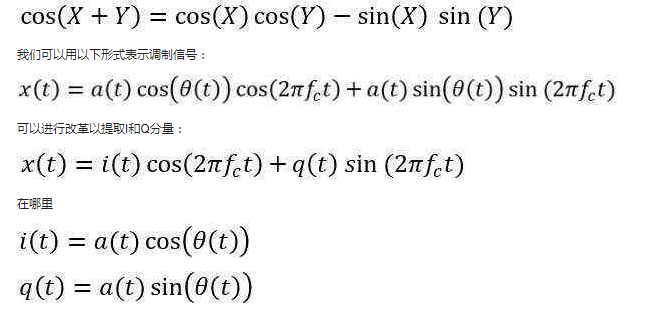

图1以图形方式显示了这一点，其中I分量在水平轴上，而Q分量在垂直轴上。这种格式对EE来说应该很熟悉，它基于正弦和余弦函数之间的90度相位偏移。

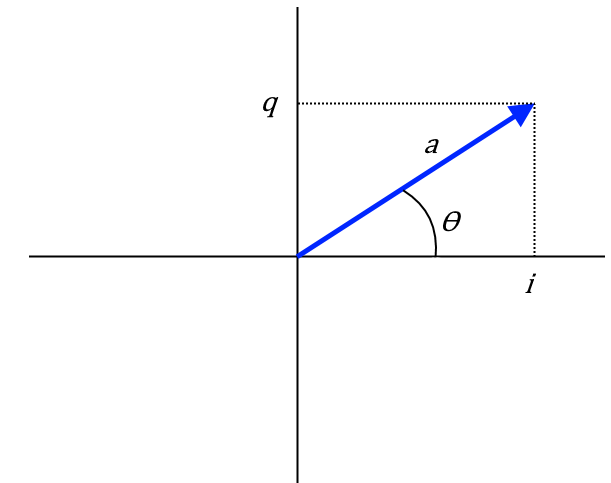
图1：矢量图表示调制信号的幅度和相位。（改编自参考文献1）

通过以下等式，调制信号的幅度和相位与I和Q分量相关：

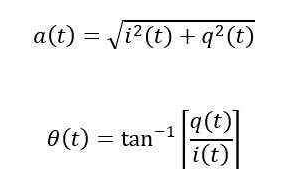
我在方程式中保留了“（t）”，以强调这些变量是时间的函数，通常会根据所应用的调制而变化。对于经典AM，可以想象矢量在长度（振幅）上变化而相位角保持不变的情况。对于PM，请想象相反的情况：矢量的振幅保持恒定，但是角度根据调制而变化。用力蹲下，您可以看到矢量实时移动。

现在，这似乎只是一堆琐事，但正交调制通常是在具有框图的系统中实现的，如图2所示。

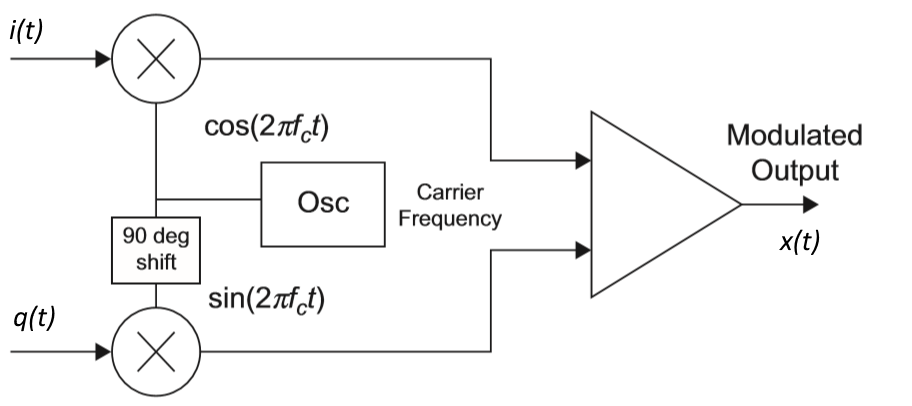
图2：正交调制器使用正弦和余弦函数来调制振荡器的载波。

我们可以将i（t）视为控制同相（余弦）部分，将q （t）视为控制正交（正弦）部分。将它们加在一起可创建所需的输出信号。可以使用模拟或数字技术（或两者的组合）来实现此框图。已经使用这两种方法创建了实用的系统，但是毫不奇怪，明显的趋势是使用数字电路和数字信号处理。

图2表示正交调制系统的发送端。在接收端，将有一个相应的正交检波器，该检波器从调制波形中提取I和Q信号。

数字调制
正交调制可用于实现无数种调制方案，但对于数字调制具有最大的价值。例如，使用向量的相位的数字调制被称为相移键控（PSK）。

图3显示了PSK的两个示例：4-PSK使用四个不同的相位来产生四个调制状态。（请注意，幅度保持恒定。）图3仅显示了矢量的尖端将落在的位置，这是显示这些状态的常用方法。这种类型的图通常称为星座图。因为调制格式具有四个可能的状态，所以每个调制状态都可以表示两个二进制值（在图中显示为00、01、10、11）。

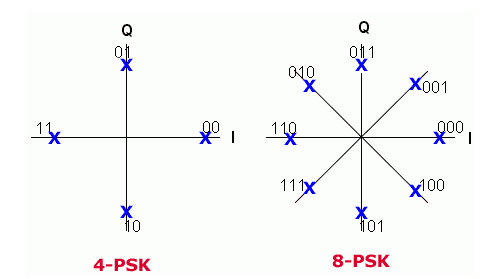
图3：简单PSK信号的星座图（来自参考文献3）

图3还显示了8-PSK，它使用相位调制来创建八个调制状态。该图显示了三位的逻辑状态。具有更多的调制状态可以使系统在给定的时间内传输更多位的信息（以存在噪声的情况下增加的错误率为代价）。

正交幅度调制（QAM）同时使用幅度和相位来添加其他调制状态。图4显示了16-QAM（具有16种状态）。想象一下我们的调制矢量在跳动，基于数字调制指向这些状态中的每一个。为了简化起见，图中未显示逻辑值，但是将调制状态映射为16个值，代表4位信息。

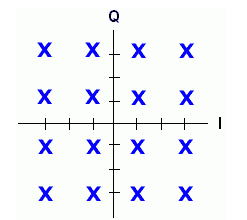
图4：16-QAM信号的星座图（来自参考文献3）

FM呢？
如您所见，调制载波的幅度和相位是创建调制载波的一种灵活方法。尽管FM是1920年代的一种古老技术，但今天仍然在广播和陆地移动无线电等应用中使用FM。我们如何使用正交调制实现FM？

通常，瞬时频率是瞬时相位的导数（参考文献4）。

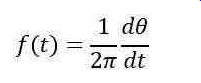
其中f（t）是瞬时频率，θ（t）是瞬时相位。

对于FM，瞬时频率必须根据调制信号而变化。

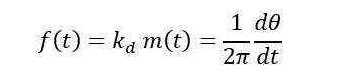
其中k d 是偏差常数，m（t）是调制信号。

解决所需的相位信号，我们得到：

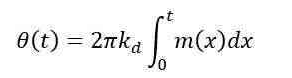
该结果表明，我们可以通过提供作为调制信号不可或缺的相位调制来创建FM信号。（是的，我忽略了积分的初始条件。）

可以使用模拟积分器或等效的数字算法创建所需的PM信号。因此，正交调制器可以使用PM产生FM信号。

正交调制和I / Q信号广泛用于电子通信系统中。特别地，数字调制充分利用了正交调制系统。但是，可以产生任何基于载波的调制，包括传统调制类型，例如AM和FM。I和Q数字流的概念由于其灵活性而在许多电子通信系统中使用，并已成为表示调制信号的事实上的标准。

参考

• 频谱和网络测量（第2版），第6.12节“正交调制”，Robert A. Witte，科学与技术出版，2014年。
• “通信系统中的数字调制-简介”，应用说明，出版号5965-7160E，是德科技，2014年。
• “调制方案：使用模拟信号移动数字数据”，EE Times的安德鲁·戴维斯（Andrew W. Davis），EE Times，1997年10月4日。
• “瞬时相位和频率”，维基百科。

编辑：hfy