浅谈控制系统设计的波特图，相位裕度

稳定性和波特图

自从电子通信问世以来，频率响应一直是大多数仪器的常用测量单位。即使在引入反馈放大器之后，频率响应仍然是确定稳定性的基础。波特图已成为可视化电路频率响应以确定系统是否不稳定的重要资源。

因为系统根是以因子形式提供的，所以在这种情况下，我们必须检查分母以观察实部是正还是负。但是，只有在我们知道闭环传递函数的情况下才能做到这一点。通常，闭环传递函数是未知的。在闭环传递函数未知的情况下，我们可以通过评估开环传递函数texKG（jomega）[/ tex]并对其进行测试来确定稳定性。在这里，我们不必考虑闭环传递函数。

稳定保证金

大多数控制系统设计在稳定性方面表现相似。通常，如果增益超过某个临界点，系统就会失去稳定性。增益裕度和相位裕度都可以衡量系统的稳定性裕度。这两个量直接与以下稳定性条件方程式有关：[tex] left | KG（jomega）右| <1 [/ tex]，处于[tex]角G（jomega）=-180 ^ {circ} [/ tex]

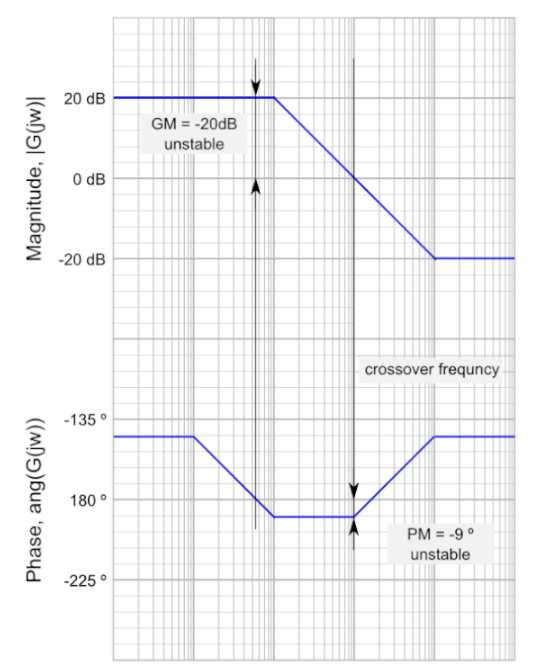
波特图不稳定示例

获得保证金

增益裕度（GM）是增益小于中性稳定值的因数。通常，我们通常可以直接从波特图上读取增益裕度。这是通过计算[tex] left | |之间的垂直距离来完成的。KG（jomega）右| [/ tex]曲线，[tex]左| KG（jomega）右| = 1 [/ tex]的频率为tex角G（jomega）= 180 ^ {circ} [/ tex]。

相位裕度

与确定稳定裕度有关的另一个数量是相位裕度（PM）。这是衡量给定系统满足稳定性条件的好坏的另一种方法。相位裕度由[tex] left | | tex的相位超过tex-180 ^ {circ} [/ tex]多少决定。KG（jomega）右| = 1 [/ tex]。上图显示，要使系统稳定，需要一个正PM。从图中可以看出，GM表示增益在系统变得不稳定之前可以增加的量。通过测量当texKG（jomega）[/ tex]越过圆[]时，测量texG（jomega）[/ tex]与tex180 ^ {circ} [/ tex]之间的差来计算PM。 tex]左| KG右| = 1 [/ tex]。稳定情况接收到相位裕度的正值。

交叉频率

在输入和输出均处于相同电压电平且阻抗不变的情况下，因数1的增益（等于0 dB）被称为单位增益。当增益为该频率时，通常称为交叉频率。频率响应设计是可行的，因为我们可以轻松评估增益变化如何影响系统的某些方面。利用频率响应设计，我们可以确定任何texK [/ tex]值的相位裕量，而无需重绘幅度或相位信息。我们所要做的就是指出[tex]左| | |的位置。KG（jomega）对| tex [K] / [tex]的某些试验值| = 1 [/ tex]

编辑：hfy