

仿真反射详解:什么叫场的角度理解分立器件?
描述
在国外能碰到许多二三十年工作经验的工程师,帮助他们沟通的工具不是PPT,不是仿真结果,不是测试结果,而是一张纸和一支笔。
很佩服他们可以用一张纸一支笔给你勾绘出一个电路,一条波形,一种debug的方案。曾有一个老工程师告诉我,当你用场的角度去理解电路上的器件的时候,一切将会变得简单起来。
什么叫场的角度理解分立器件?在这个世界里,容抗是Xc=1/(2πfC) ,感抗是XL= 2πfL=ωL 。
这两个公式中的f与ω指的不是我们的信号频率,而是正弦波的频率与角频率。
在这里,我们要感谢伟大的让•巴普蒂斯•约瑟夫•傅立叶——简称傅立叶,对,就是发明傅立叶变化的那个人。
所以在大家眼中看到的信号是这样的:
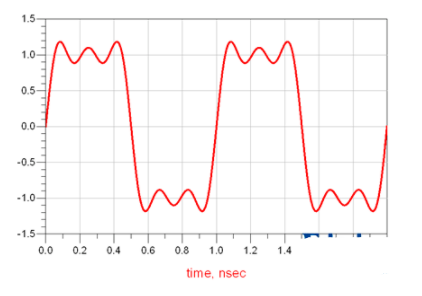
而在一个SI工程师的眼中看到的信号是这样的:
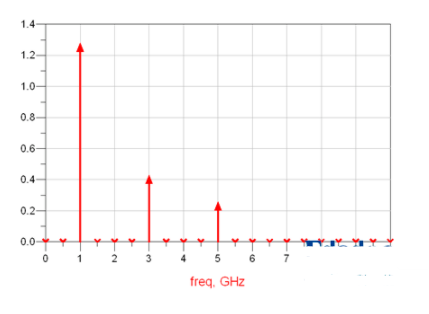
或者,这样的:
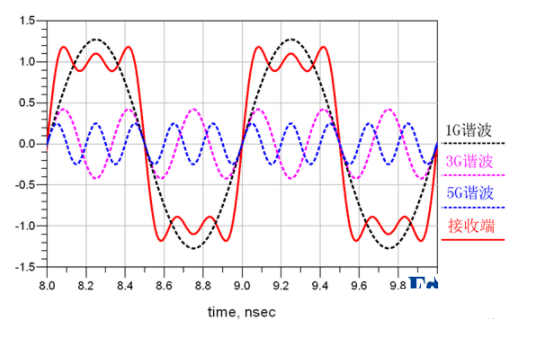
当我们能将信号分解为一个一个正弦波来研究的时候,一切都变简单了,可以量化了。在正弦波的世界中只有频率f,幅度A,相位θ。
现在,我们可以愉快的用场来看这个世界了。
让我们来思考下面这个问题:
一个1V的正弦波在某岔路口分成了两个大小相等的正弦波,两条路通向同一个终点,但是一条路长为L,另外一条路长度为L+X,在终点的时候,这个正弦波变成了什么?
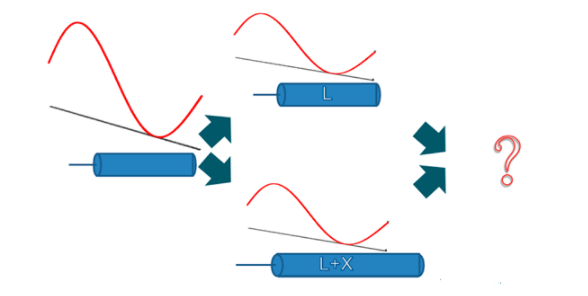
当两条岔路一样长时:
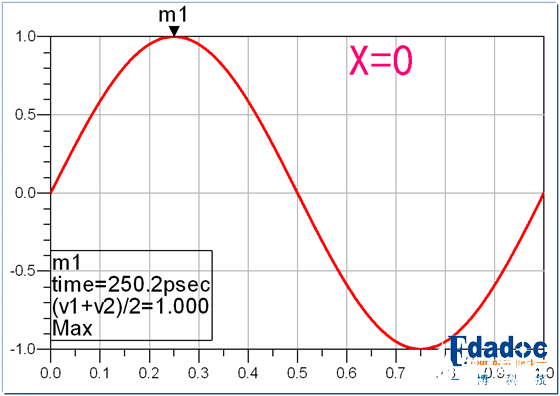
终点的信号和起点的信号没有区别。
当一条路比另一条多二十分之一波长时:
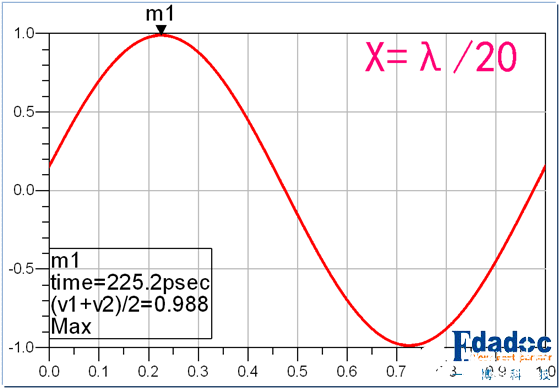
区别也十分小吧?高速先生在这里特别打上了mark点。大家可以看到,终点的信号比起点的信号衰减了1.2%。
X更长,达到八分之一波长时:
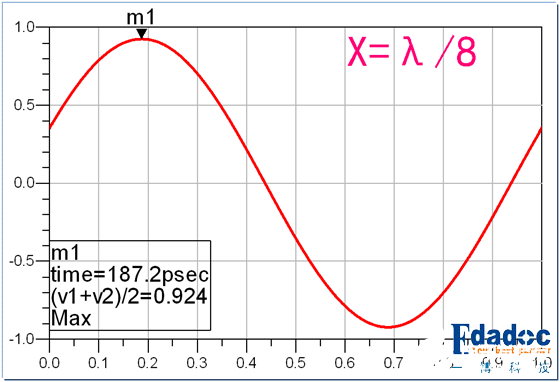
这时候,衰减已经不需要打mark点也可以看出来了。
X再长一点,达到四分之一波长时:
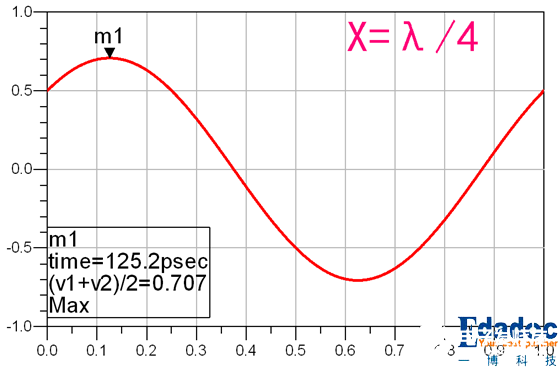
30%的能量不见了!
直到,X达到波长一半的长度:
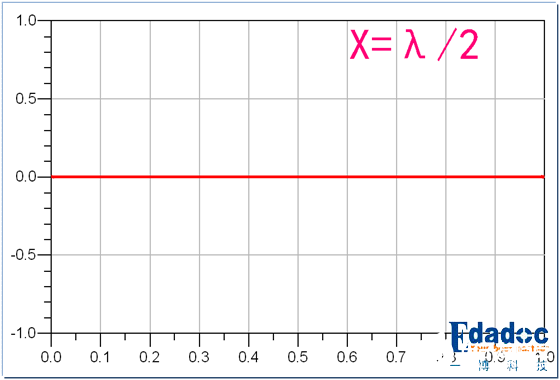
好惨,完全阵亡。
那么,这一期的问题是:为什么高速先生要举这个例子呢?
集总的世界
大家知道,信号是以电磁波的形式传递的。
波从一个介质入射到另一个介质时,会产生反射。同样的,当我们信号传输遇见阻抗不连续时,信号会产生反射。
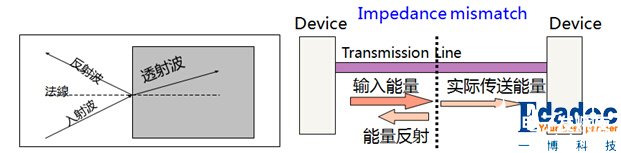
反射能量的强度跟阻抗比匹配的程度相关。在开路短路这种极端情况下,反射的幅值会和入射的幅值相等。
由于反射的存在,即使我们的设计中通常不会出现前面例子中分叉之后再接到接收端的情况,还是会有大量相位不相等的谐波在我们传输线中传输。
这些能量就会相互产生干扰,受干扰的程度跟反射的幅值和两个能量之间的相位差有关。
从前面的例子中我们可以看到,当两个信号的相位差不到λ/20时,叠加后的影响是微乎其微的。
大家通常将λ/20作为一个界限,当传输线长度小于λ/20时,我们用集总参数来考虑我们的电路。
我们一直在说λ,那λ是什么?如果大家每次都想着λ=v*T=v/f的话,理解一些理论的时候肯定很绕,没法有个直观的反应。在这里大家需要再建立起一个概念,我们通常看到的波形是一个电压/时间的坐标轴,当我们把X轴的时间换成长度,在普通的FR4板材上,我们看到的大致是一个这样的图像:
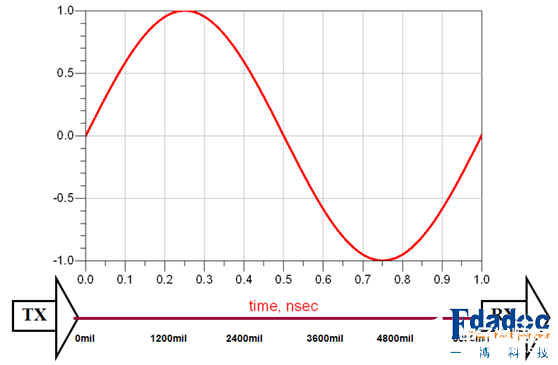
我们要在一条传输线上完成一个1GHz的正弦波,这条传输线大概需要6000mil。
所以很多时候我们以为我们传输线上的波形是这样子的:
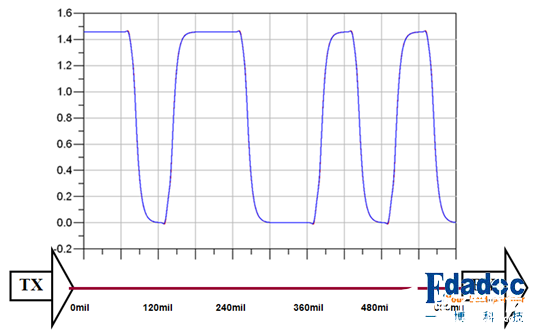
但其实我们传输线上实际的波形可能是这样子的:
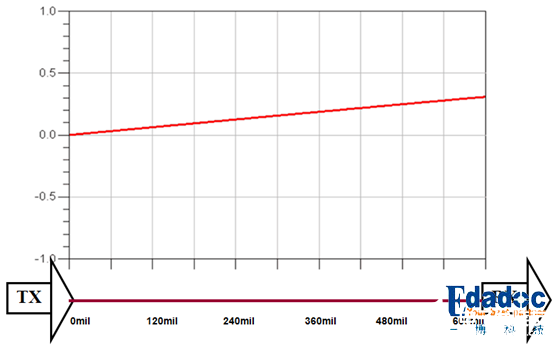
或者是这样子的:
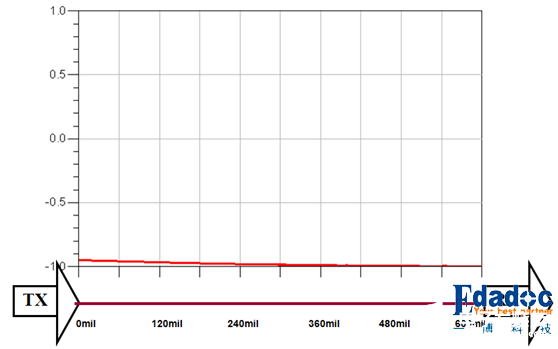
可以看到其实他们的dv/dX是非常小的,这里用dX不用dt是因为传输线的总电容/电感是跟X有关的。
我们都知道地球是圆的,可是身处我们的位置去看的话地球就是平的。同样的,在集总参数中,由于在线路上的电压电流变化速度很慢,我们可以将它当做是直流,在这时,传输线的容抗与感抗都没有表现出来,这时传输线是透明的:
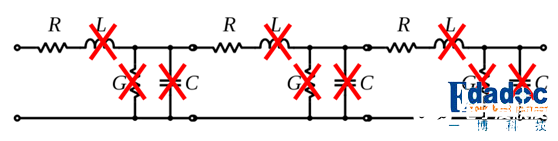
接收端接收到的就是发送端发出的信号,下面是传输线10Ω与传输线100Ω的对比:

为什么以前的板子不需要控阻抗,为什么现在的一些模拟信号也是不需要控阻抗的,原因就在这里。
通常我们1GHz的正弦波的λ/20在300mil左右,10MHz的正弦波的λ/20则有30000mil。
传输线是透明的,接收端接收到的波形与传输的路径没有关系,这就是集总的世界。
编辑:hfy
-
半导体分立器件有哪些 分立器件和集成电路的区别2024-02-01 6800
-
从仿真器的角度理解Verilog语言12023-05-25 1495
-
一文详解分立元件门电路2023-03-27 4578
-
分立器件是什么?2023-02-24 20300
-
分立器件的实现的细节2021-10-28 1525
-
紧缩场反射面在feko中的建模2021-07-23 16726
-
请教IGBT器件场截止层、场板的原理和作用是什么2020-02-20 6534
-
详解PCB设计路和场的反射2019-05-24 2265
-
分立器件行业概况,分立器件行业现状2018-09-28 26843
-
有哪位大神可以帮忙给详解下该电路中各部分元器件分立及组合的作用?2016-11-25 3350
-
基础理论之反射详解2015-06-15 6419
-
MATLAB通信仿真及应用实例详解2010-02-08 1240
-
半导体分立器件的命名方法2008-12-19 1799
全部0条评论

快来发表一下你的评论吧 !

