

接收器的双边带(DSB)和单边带(SSB)噪声图测量示例
描述
系统和设计工程师通常使用噪声系数来确保最佳信号性能。但是,在信号链中使用混频器给直接的噪声图分析带来了挑战。本教程首先检查噪声系数的基本定义,然后继续对包括混频器的级联模块进行基于方程的分析,然后再采用典型的实验室技术来测量噪声系数。在探索将Y因子方法用于混频器噪声图测量之前,本教程还涵盖了噪声温度和Y因子噪声测量的概念。讨论了双边带(DSB)和单边带(SSB)噪声图测量的示例。
简介
本教程解决了现代无线电接收机中的噪声系数问题。它讨论了导致接收机系统中NF的最常见因素,以及有助于实现所需测量结果的数学方法。探索了无线电接收机的不同部分,并重点介绍了每个部分的NF分析。
噪声系数的一般概念已得到系统和电路设计人员的充分理解并广泛使用。特别是,它用于传达产品定义者和电路设计人员对噪声性能的要求,并预测接收器系统的整体灵敏度。
当混频器是信号链的一部分时,就会出现噪声图分析的主要困难。所有实际混频器将RF频谱折叠在本地振荡器(LO)频率附近,从而产生一个输出,其中包含根据fOUT = | fRF – fLO |两侧频谱的总和。在外差架构中,这些贡献之一通常被认为是虚假的,而另一贡献是预期的。因此,很可能采用图像拒绝滤波或图像消除方案来大大消除这些响应之一。在直接转换接收器中,情况有所不同。两个边带(高于和低于fRF = fLO)都被转换并用于有用信号。因此,这确实是混频器的双边带(DSB)应用。
工业中通常使用的各种定义在不同程度上解释了噪声折叠。例如,传统的单边带噪声因子FSSB假设允许来自两个边带的噪声折叠成输出信号。但是,只有一个边带可用于传送所需信号。假定两个响应的转换增益相等,自然会导致噪声系数增加3dB。相反,DSB噪声系数假定混频器的两个响应都包含有用信号的一部分,因此,噪声折叠(以及相应的信号折叠)不会影响噪声系数。DSB噪声系数可用于直接转换接收器以及射电天文接收器中。然而,更深入的分析表明,对于设计人员来说,仅针对给定的应用选择合适的噪声系数“风味”,然后在标准Friis方程中替换相应的数字是不够的。这样做会导致分析上的错误,如果在确定系统噪声系数时,混频器或混频器之后的组件起着不可忽略的作用,则分析可能会变得尤为严重。
混合器噪声的概念模型
可视化混合器噪声贡献的一种方法是考虑混合器的概念模型(图1)。该模型基于安捷伦Genesys仿真程序提供的模型。
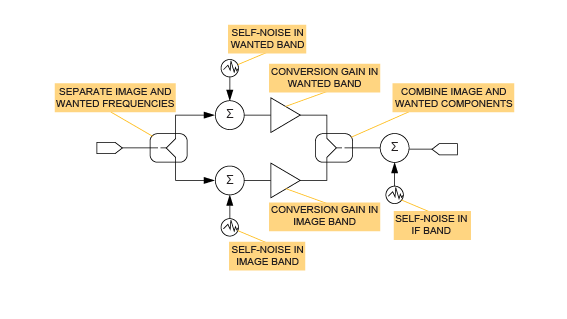
混频器噪声贡献。
在此模型中,输入信号分为两个独立的信号路径,一个代表LO上方的RF频率,另一个代表LO下方的频率。每条路径在混频器中都要经过独立的加性噪声处理,并且要应用独立量的转换增益。最后,两条路径被转换为IF频率,并与混频器输出级中可能产生的其他噪声贡献相加。在所需频带和图像频带中,每单位带宽的自噪声功率可能会不同;相应的转换增益也可能不同。
为方便起见,我们可以将所有噪声源引用到输出,并以全局噪声项NA进行收集,NA表示从混频器输出端口获得的每单位带宽的总附加噪声功率。
NA = NSGS + NIGI + NIF
请注意,NA完全不取决于混频器输入端口上信号的存在与否。
总结了混频器的内部噪声源之后,我们现在来看归因于源端接的噪声(图2)。我们确定了两个离散的噪声源,分别代表由于输入端在所需频率和镜像频率处的输入而引起的输入噪声密度。我们必须将它们视为独立的数量,因为应用电路会导致其中一个衰减,而另一个会以低损耗传输到混频器的RF输入端口。如果图像和所需的RF频率很好地分开并且采用了频率选择匹配,则可能是这种情况。
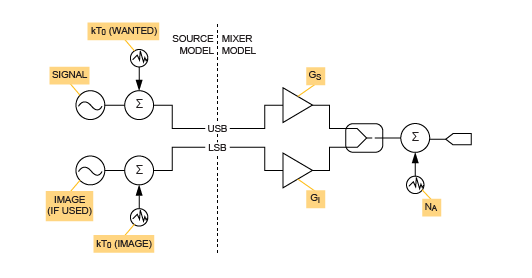
源噪声和混频器噪声贡献。
在宽带匹配的情况下,我们可以写为NOUT = NA + kT0GS + kT0GI。但是,如果在所需的RF频率下对混频器进行高Q频率选择匹配,则由于源端接在镜像频率处而在输出端产生的噪声可能可以忽略不计,从而导致NOUT = NA + kT0GS。通常,我们可以将系数α分配给在镜像频率下可用于混频器输入端口的输入源端接噪声功率的有效分数。因此,NOUT = NA + kT0GS +αkT0GI,其中α是0≤α≤1范围内的特定应用系数。稍后我们将看到应用中的有效噪声系数取决于α的值。
异源接收器
我们可以通过图3中的示例看到如何在较大的级联分析中应用有效噪声系数。要计算整个链的级联噪声系数,我们需要封装混频器及其相关的LO和图像抑制滤波,如下所示:具有特定增益和噪声系数的等效两端口网络。该两端口网络的有效噪声因子为FSSBe = 2(FDSB – 1)+ 1,因为前面的滤波器很好地抑制了图像频率处的终端噪声。
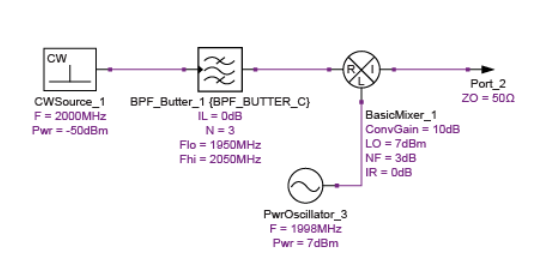
在相邻系统块的上下文中,外差混频器。
请注意,适用的噪声系数既不是混频器的DSB噪声也不是SSB噪声系数。相反,它是一个有效的噪声系数,介于这两个值之间。在这种情况下,DSB噪声系数为3dB,如上所述,两端口网络的等效噪声系数可以计算为4.757dB。如下表所示,在整体级联计算中使用该值会导致系统噪声系数为7.281dB。手动计算表明,此结果与标准Friis方程式一致,混频器噪声系数为4.757dB。

系统中外差混频器的级联性能模拟
通常,当用等效的两端口网络代替混频器及其相邻组件时,输入端口应该是信号流中拒绝图像响应的最新节点。输出端口应该是图像和所需响应组合在一起的最早节点(通常是混频器的输出端口)。如果该架构无法有效地抑制混频器的图像响应,则未经修改就无法使用Friis方程。
结论
在本教程中,我们看到,在混频器属于接收器级联的一部分的情况下,使用混频器噪声系数的DSB或SSB版本,级联噪声因子的Friis公式通常无效。如果使用滤波器在很大程度上消除了接收器的图像响应,则可以用等效的两端口网络代替混频器,滤波器和LO子系统。但是,必须考虑到耦合到混频器输入端口的源端接的频率选择性,由DSB噪声系数计算得出的噪声系数。
我们还发现,相同的物理结构可能具有不同的有效噪声系数,具体取决于信号是分布在LO周围还是完全分布在LO的一侧(即,应用分别是DSB或SSB)。通过在LIF模式下使用复杂的接收器而导致的SNR的3dB损失可以(通常)通过适当使用镜像抑制合并,复杂滤波或等效基带处理来恢复。
Y因子测量将评估混频器的DSB噪声系数,除非采取特殊措施滤除镜像频率处的宽带噪声刺激。这是与先前导出的级联方程一起使用的适当值。当使用滤波器尝试获得SSB噪声系数时,有必要考虑所用滤波器的插入损耗。此外,通过滤波器抑制源端接图像噪声的程度可能会导致偏离SSB噪声系数的经典定义。匹配衰减器的使用可以在很大程度上克服此问题,前提是所使用的衰减量与噪声源的ENR相比不会过多。
编辑:hfy
-
TC-ModBox-SSB系列载波抑制单边带调制模块2023-03-08 872
-
单边带技术2010-09-15 1050
-
什么是单边带?什么是ssb?2008-09-06 17847
-
双边带AM调制器电路2009-03-20 1112
-
单边带调制2010-05-18 2372
-
一文看懂单边带和双边带的波形及区别2018-03-13 153231
-
单边带调制(SSB)信号的产生设计实验资料说明2019-01-29 4092
-
双边带调制原理_双边带调制的优缺点2020-03-11 24911
-
单边带调幅对讲机设计2021-03-18 1571
-
GB/T 15960-1995 短波(HF)广播单边带制式技术规范2023-02-01 929
-
NI Multisim 10经典教程分享--抑制载波双边带调幅(DSB/SC AM)解调电路2023-02-16 3820
-
单边带调制和双边带调制的区别2024-08-14 8148
全部0条评论

快来发表一下你的评论吧 !

