

降压型变换器的分叉及其混沌行为的研究
嵌入式设计应用
描述
降压型变换器的分叉及其混沌行为的研究
DC/DC变换器运行中产生大量的非线性现象,主要是功率器件开关引起的[1]。已有研究表明,在DC/DC开关变换器实际运行中,时常会出现一些奇怪或不规则现象,如不明的电磁噪声、临界运行状态的突然崩溃、系统运行的不稳定和无法按实际要求工作等现象,这些现象是DC/DC变换器固有的非线性特性--分又和混沌现象的一种外在表现[2,3]。DC/DC变换器一旦进入混沌工作状态,由于混沌运动的不确定性将导致系统运行状态的无法预测和控制,甚至完全无法工作。因此,功率变换器分叉和混沌现象的研究,对于避免、消除和利用混沌具有非常重要的指导意义。文献[4]分别用输入电压和负载电容作为分叉和发生混沌的参数进行了仿真试验。选取电压反馈系数作为分叉和发生混沌的参数,通过调整反馈参数,可以实现各种周期轨道的稳定控制。由于系统处在周期运动区时,其电压转换效率高于系统处在混沌运动区时的电压转换效率,因此研究这种电路系统的混沌控制具有重要的实用价值。
1 Buck变换器的基本电路和非线性动力学方程[5]Buck变换器是一种输出电压等于或小于输入电压的单管非隔离直流变换器。其主电路的示意图如图1所示。
 |

其中,Uo,Io,Us,Is分别是输出电压、输出电流、输人电压、输入电流的平均值,D是晶体管的导通比。
考虑电路在不连续工作模式(DCM)情况下,电路出现3种工作模式(见图2):
 |

模式2: 即S关断,VD导通时,此时的等效电路如图2(b),根据等效电路得到:

模式3:即S关断,VD截止时,此时的等效电路如图2(c)所示,根据等效电路得:

由式(2)~式(4)得到断续状态的Buck电路状态方程为:

其中:

2 Buck变换器的精确离散模型
如图3所示为Buck变换器的原理图。图3中Us为输入电压;s为开关器件;VD为续流二极管;iL为电感L上流过的电流;Uc为电容电压;Uo为负载两端输出电压;D为稳态工作时开关占空比,他等于S导通时间与开关工作周期T之比;dm是第m个开关周期占空比,当稳态工作时dm=D;△dm是第m个开关周期占空比变化量;K是变换器比例反馈参数。在一般不连续模式下,电路的状态方程可以用式(5)表示。求解式(5)得:
ti-1<t<to为初始时刻,对他每个开关周期(即在t=t1,t=t2,t=t3 时刻)进行一次状态变量的采样,得到离散序列{χm+1},m=0,1,2,…由式(6)可以得到一个从χm到χm+1的离散映射: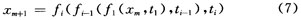
其中△ti=ti-ti-1为每个开关模态的时间间隔,其大小取决于变换器反馈控制规律。DC/DC Buck变换器的控制率为:

式(8)中Uom是第m周期的输出电压,即反馈电压,dm为第m个开关周期占空比。式(8)中当dm≤0,取dm=0;当dm≥1,取dm=1;当0<dm<1,取dm=dm。
由式(6),(7)可以得到DCM情况下的离散模型为:
△t-to=dmT对应状态1的工作时间;  对应状态2的工作时间;△t3=t3-t2=T-△t1-△t2对应状态3的工作时间;T=tπ+1-tm表示电路开关的周期。
对应状态2的工作时间;△t3=t3-t2=T-△t1-△t2对应状态3的工作时间;T=tπ+1-tm表示电路开关的周期。
 |
由于离散迭代映射中存在矩阵指数,且要对其求积分,要得到其精确的离散映射有较大的难度。在这里引入凯莱-哈密尔顿定理,则式(10)中的eAit,一可表示为:
其中ao(ti)和a1(ti)满足方程:
式(10)中A的2个特征值分别为λ1,2,由此可以得到:

其中:
将eA1t,eA2t2,eAA3t3带入式(10)得到Buck变换器的精确离散模型:
3 Buck变换器中分叉与混沌现象动态演化过程
DC/DC开关变换器以往的建模方式都是采用近似等效、线性化的方法,从而能利用较成熟的线性系统理论对其模型进行研究。但不能展示DC/DC开关变换器非线性混沌现象,对开关变换器的开关非线性动态过程做细致的分析,研究表明需采用非线性离散模型[6]。
DC/DC Buck变换器工作在不连续工作模式(DCM)。用Matlab对图3进行仿真,根据前面建立的精确离散模型,将反馈参数K从0开始不断变大,其他参数如下:Us=33 V;R=12.5 Ω;L=208μH;C=222 μF;T=333.33 μs;Vo=25 V;rc为电容内阻,rc=0.0124,P=50 W。
图4是该离散模型的仿真结果,由图可见,随着反馈参数k的增加,Buck变换器表现出如下动力学行为:当K△0~0.134 5,系统呈现1周期运动;在K△0.134 5时,出现分叉现象,当K△0.184 6时,出现第二次分叉,在KA0.197 9~O.248 5范围内,存在2个混沌窗口;当K△0.248 5时,系统又经过边界碰撞分又,出现3周期运动,然后经过倍周期分叉,当K△0.661时进入混沌状态,但在混沌区中存在大量的周期窗口。从图中可以看出变换器从稳定工作,到周期分叉和进一步周期分叉,最后进入混沌状态,完整地展现出Buck DC/DC变换器从稳定、不稳定直至混沌演化的全过程。
4 DC/DC Buck变换器中分叉运动的稳定性分析
DC/DC Buck变换器离散系统的稳定性主要取决于系统在不动点处雅可比矩阵的特征值的大小,只有当他的特征值的绝对值都小于等于1时,系统就是稳定的。所以,由式(6)得到DC/DC Buck变换器离散系统在稳定点X的判别式为:

其中△χm+1=χm-X,△χm为系统扰动,当△χm很小时,上式的高阶项很小,可以忽略不计,所以DC/DC变换器的稳定性判据可简化为:

DC/DC Buck变换器(当他的主要参数确定后)的稳定性直接取决于控制系统的设计。如图3所示,K是DC/DC Buck变换器比例反馈参数,他的取值直接影响变换器的稳定性。将上述仿真试验时选取的参数代入式(12),以反馈参数K为分叉变量,与电压反馈参数K相关的稳定性判别式可由式(14)得到:
由式(15)可以得到K的临界稳定值为:Kc=0.133 5。对系统稳定性而言,当K<Kc时,系统稳定,反之,系统不稳定,且开始出现倍周期分叉逐渐进入混沌状态,这更有力的证实了前面的仿真结果与理论完全相符。
 |
5 结 语
本文对DC/DC Buck变换器的分又及其混沌行为进行进一步深入研究,研究结果表明:电压反馈系数K对该电路系统的动力学行为有十分重要的影响。当K△0~0.134 5,系统呈现1周期运动;在K△0.134 5时,出现分叉现象,当K△0.184 6时,出现第二次分叉,在K△0.197 9~0.248 5范围内,存在2个混沌窗口;当K△0.248 5时,系统又经过边界碰幢分叉,出现3周期运动然后经过倍周期分叉,当K△0.661时进入混沌状态,但在混沌区中存在大量的周期窗口。仿真结果表明,DC/DCBuck变换器存在着较大范围的非线性行为,当反馈参数变化时,系统就沿着倍周期轨迹运动,并最终进入混沌仿真结果与理论结果完全一致,仿真和理论分析证明所建立的DC/DC Buck变换器的精确数学离散模型的正确性能真实反映变换器各变量间的解析关系,从而为DC/DCBuck变换器的优化设计和控制提供了理论依据。
- 相关推荐
- 降压型
-
LLC谐振变换器的研究2018-07-26 0
-
DCDC降压型BUCK变换器应用于汽车电子系统中的设计技巧有哪些?2021-07-28 0
-
电流模式控制BOOST变换器中的切分叉及阵发混沌现象2010-06-23 525
-
开关型功率变换器的研究与设计2009-07-07 1540
-
采用HS7076构成的降压型DC DC变换器电路2009-11-14 965
-
周期性扩频的Boost变换器中非线性现象的研究2013-09-26 554
-
H桥变换器中分岔与混沌现象的研究进展与趋势2016-05-06 564
-
COT架构降压型变换器片上纹波补偿电路_高峡2017-01-08 792
-
Buck变换器中的快标分叉控制研究_胡乃红2017-03-19 649
-
降压型功率变换器LM2596的原理及应用2017-09-12 1038
-
DC-DC开关变换器混沌现象及其应用研究动态和进一步设想2017-09-15 794
-
降压变换器的作用及应用介绍2018-08-10 7360
-
LTC1626:低压高效降压型DC/DC变换器产品手册2021-04-20 544
-
DN269-60V降压型DC/DC变换器保持高效率2021-04-27 703
-
XL7015-降压型直流电源变换器芯片2021-09-15 1929
全部0条评论

快来发表一下你的评论吧 !

