

采用CPLD器件MAX7128实现温度控制系统的应用设计
可编程逻辑
描述
“温度”是各类工业控制生产中常见的、而又十分重要的控制参数。人们研制出各种针对不同控制对象的温度自动控制系统,其中软件控制算法已比较成熟,但温度控制系统的硬件构成特别是功率控制部分往往存在着硬件结构复杂,分离元件较多,结构较为封闭等问题。随着CPLD器件的大规模运用,采用CPLD器件可简化控制系统的硬件结构。本文设计了一种以8051单片机为核心的温度控制系统,该系统的控制部分由CPLD来完成,针对不同的控制对象可采用不同的控制算法,因此该控制系统具有结构开放、成本低廉、性能可靠等特点。
1 系统硬件构成
对一个温度自动控制系统来说,其硬件结构由两大部分构成:温度测量部分和功率控制部分。系统结构总框图如图1所示。
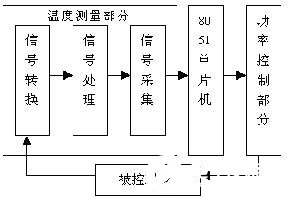
图1 系统总框图
1.1 温度测量部分
(1)信号转换电路:根据被控对象的不同,采用不同的温度传感器,将物理信号变换为电信号,以便8051单片机处理。
(2)信号处理电路:由传感器所变换得到的电信号一般为小的电压信号,受到控制精度的限制,不能直接送入到A/D,而需要对小信号进行放大。本系统中采用了程控差分放大器,其电路图如图2所示。差分放大器A3采用高精度运放AD844;前置放大器A1改变了小信号的测量精度以及传感器和差分放大器的匹配;射级跟随器A2则实现了D/A和差分放大器的匹配和缓冲;由于小于1.2V的低阻驱动的电压基准源难以获得,因此采用16位D/A转换器MAX542构成数控基准源,整个数控基准电压源的最大输出为2.5V,其最小分辨率为2.5V/216≈0.04mV;根据传感器输出电压信号的范围确定差分放大器的放大倍数,这样就构成了整个程控可变增益差分放大器。该程控放大电路不仅克服了传统程控放大器增益分档不够多的缺点,还具有高精度,控制容易等优点,因此系统的测量精度、控制精度得到了提高。
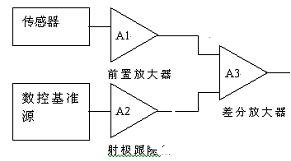
图2 信号处理电路部分
(3)信号采集电路:该部分电路由12位的A/D转换器构成。A/D转换器的字长,决定了系统的控制精度,字长越大,控制精度就越高,但综合考虑系统控制指标以及控制效率,采用12位的A/D转换器即可,其转换精度可以达到±0.012%。在本系统中我们采用MAXIM公司近年推出的高速A/D转换器MAX197,与一般A/D芯片相比,品质因素高、外围电路简单并具有标准的微机接口,数据总线的时序与绝大多数通用的微处理器兼容,全部逻辑输入和输出与TTL/CMOS电平兼容。
1.2 功率控制部分
常见的功率控制有两种方法:一是调功,通过控制单位时间内加在功率器上的正弦波的波头数来控制功率;二是调相,通过控制可控硅的导通角,来控制导通时加在功率器上的电压幅值,实现对功率器的精确均匀控制。由于方法二可以均匀精确的控制功率,并能够对功率进行微调,使得被控对象的温度平滑地到达设定值,因此在本系统中选择方法二。其控制电路的电路框图如图3所示,图中方框内的硬件部分由CPLD器件实现,具有简洁,性能可靠等特点。
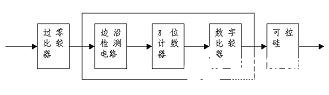
图3 温度控制电路框图
利用调相法控制功率,必须随时知道并记录220V市电的相角,从而准确的控制导通时刻。在传统的控制系统中一般利用模拟锁相环电路提取市电的同步信号,但加大了电路构成的复杂程度。在本系统中省去了模拟锁相环器件,简化了电路结构。硬件电路描述如下:
(1)采用变压器将220V市电转换为同步的峰值为5V的正弦波电压信号,然后经过过零比较器把正弦波电压信号转换为占空比1:1的50HZ方波信号。
(2)50HZ的方波信号通过边沿检测电路得到同相的100HZ的窄脉冲信号,其边沿检测电路原理图如图4所示。
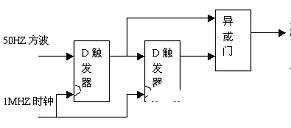
图4 边沿检测电路
(3)8位计数器对25KHZ的频标信号进行计数,计数器具备一个上升沿清零端,该端的接入信号为(2)中得到的100HZ的窄脉冲,该窄脉冲以频率100HZ对计数器清零,使得计数的开始时刻为50HZ市电信号的过零处,从而保证严格同步。具体信号时序关系如图5所示。
(4)8位计数器的计数值输入到数字比较器中,与单片机设置的预定值进行比较:当计数值小于等于单片机输入的预定值时,数字比较器的输出端输出为高电平。当计数值大于单片机输入的预定值时,数字比较器的输出端输出为低电平。这样输出周期性的与市电半波同步的方波信号去控制可控硅的导通角,通过改变单片机输入值的大小可以方便的调节可控硅的导通角,准确地高精度地实现功率调节。
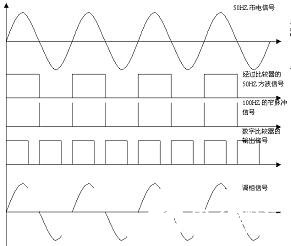
图5 信号时序关系图
从该部分硬件结构的组成特点可以看出,其组成核心是由可重新配置特点的CPLD器件 MAX7128构成。MAX7128为高性能可擦除器件,采用第二代多阵列矩阵(MAX)结构,可用门数为2500门,宏单元数为128,逻辑阵列块数为8,通过标准的JTAG接口,支持在系统可编程(ISP)。它实现了控制部分的核心功能,其它的电路都属于辅助电路。因此系统在结构上具有典型的开放性,这对实现软件的开放是一个很好的支持。
2 温度自动控制系统的软件设计
温度自动控制系统的软件算法通常是根据对象的纯滞后时间τ与对象的惯性时间常数Tm之比来确定,一般来说,当τ/Tmm》0.5时,可采用达林算法控制。在本系统中,针对不同的被控对象,可加载不同的软件算法,因此大大提高了本控制系统的灵活性。由于在工业控制过程中,大量的被控对象具有非线性、纯滞后性,采用PID控制很难获得良好的控制性能,因此本文重点讨论达林算法,用它来控制非线性、纯滞后对象具有良好的效果(被控对象一般为带有滞后的一阶惯性环节)。
2.1 dahlin算法的数学模型
被控对象为带有滞后的一阶惯性环节,其传递函数为
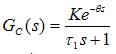
,θ=NT (2-1)
式中:
τ1 -----对象的时间参数
θ -----对象的纯延迟时间,为了简化,设其为采样周期的整数倍,即N为正整数。
K -----对象放大系数
达林算法的设计目标是使整个闭环系统所期望的传递函数Φ(s),相当于一个延时环节和一个惯性环节相串联,即
Φ(s)=
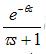
,θ=NT (2-2)
如图6所示,根据控制理论易得到带有一阶惯性对象的达林算法的基本形式:
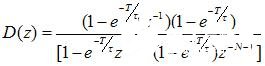
×
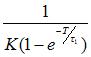
(2-3)
式中:
K -----对象放大系数
T ------ 为采样周期;
τ1 ------为被控对象时间参数;
τ ------为闭环系统的时间参数。
根据D(Z)=U(Z)/E(Z)得出差分方程:
U(K)=b1U(K-1)+b2U(K-N-1)+a0E(K)-a1E(K-1) (2-4)
其中
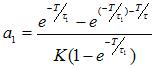
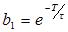
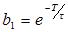
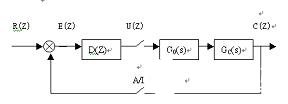
图6 控制系统方框图
2.2 dahlin算法参数的整定
(1)由系统的飞升曲线(如图7)确定对象的纯滞后时间参数θ和被控对象的时间参数τ1。
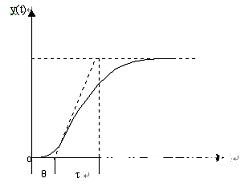
图7 被控对象的飞升曲线
(2)综合控制精度、超调量等指标选取合适的采样周期T。若T偏大,则取样稀疏,单位时间内控制点过少,势必造成较大的过冲量以及系统控制误差;若T偏小,则对采样量化字长要求过高,对于有限字长的控制系统过密的采样周期会使系统控制失败。
(3)由N=θ/T确定N值。
(4)对象放大系数K的确定。K可由下列公式确定:

(5)τ一般与T取同量级,不断调整τ值,观察系统的响应图,使得闭环系统的指标达到最佳。
3 系统应用
从该温度自动控制系统的软硬件构成可以看出,这种设计具有比较好的开放性,便于在软硬件方面进行功能扩展和重新配置,同时应用系统的构造也比较灵活。由于采用了高容量低成本的CPLD器件 MAX7128,将本系统的控制部分的核心电路的硬件资源进行了整合集成,提高了系统硬件的可靠性。针对不同的控制对象,只要适当的改变一下前端的信号处理电路,并采用满足要求的控制算法,即可胜任面对各种对象的控制任务。因此系统具备结构开放、性能可靠、灵活方便等特点,可以灵活地胜任不同对象的温度自动控制任务。
责任编辑:gt
-
基于CPLD的压电生物传感器检测电路的设计2011-01-24 2123
-
[原创]基于MAX1968的LD自动温度控制系统设计2008-07-24 5423
-
如何去设计并实现电梯控制系统?2021-04-28 1518
-
怎么利用CPLD器件及VDHL语言实现电梯控制系统?2021-04-29 1268
-
应用CPLD实现交通控制系统芯片设计2009-04-16 391
-
应用CPLD 实现交通控制系统芯片设计2009-05-14 656
-
CPLD在交流电机控制系统中的测速应用2009-05-26 535
-
基于CPLD的温度采集系统的设计2009-07-07 616
-
基于单片机+CPLD的多路精确延时控制系统设计2010-12-16 712
-
基于CPLD的电器定时开关控制系统设计2010-12-17 482
-
TMS320LF2407型DSP和EPM7128型CPLD在移动2016-05-06 694
-
如何使用CPLD进行电器定时开关控制系统的设计2019-06-11 1180
-
采用单片机和CPLD器件实现仿人手臂形假肢控制系统的设计2020-04-15 1622
-
如何实现温度控制系统的设计2020-06-08 3632
-
使用LabVIEW实现温度控制系统设计的论文研究2021-01-25 1374
全部0条评论

快来发表一下你的评论吧 !

