

单相桥式整流电容滤波负载的功率因数分析
电源设计应用
描述
单相桥式整流电容滤波负载的功率因数分析
Analysis of Power Factor to Single- phase Bridge Mode Rectifier with Capacitive Load
摘要:从理论上对单相桥式整流电容滤波负载(即非线性负载)的功率因数作定量分析,并与传
统概念的功率因数作比较。
关键词:功率因数整流滤波
1引言
功率因数一直是电力系统中比较关心的问题,近年来随着电子镇流器、开关电源等整流滤波电路的大量应用,且功率日益增大,功率因数的影响在这一领域越发明显。有些实用电路中,有适当的校正电路,但较少涉及功率因数的定量分析,本文对此作出了分析,供电路设计时参考。
2传统概念的功率因数
以往电力系统中,由于感性负载或容性负载的使用,使得交流电路中电压与电流间存在相位差,设其值为φ,其功率因数定义如下:
令:u=Umcosωt
则:i=Imcos(ωt±φ)
可见,当电压与电流相位差为φ,而波形均为余弦(或正弦)波时,功率因数只与相位差φ有关。
3单相桥式整流电容滤波负载的功率因数
单相桥式整流滤波负载的电路如图1所示。因为整流滤波电路中电容的作用,使整流桥每臂的导通时间小于半个周期,即导通角小于π,设其值为2α,如图2所示。由于i已不是正弦波,功率因数就不能用cosφ来表示。
忽略电容放电期间的压降,此时,电容可等效为一个电压源,设电压为E,内阻为r,见图3、图4,当ui>E时,半个周期中流过整流桥的电流为通常R?r,忽略ui/R项,则即流过整流桥的电流为正弦波的顶部,输入电压及电流波形如图2所示。
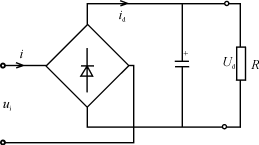
图1单相桥式整流电容滤波电路
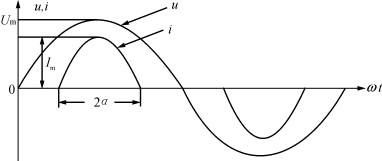
图2输入电压、电流波形
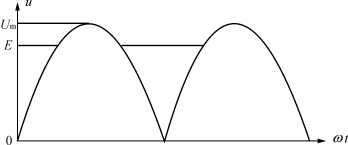
图3输出电压波形
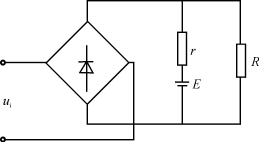
图4滤波电容等效为电压源
由图5可知:
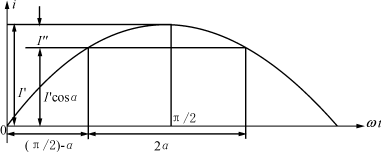
图5电流i与导通角2α之间的关系
4结论
随着导通角的增大,输入功率因数增加,当导通角2α为π时,PF=1。实际应用中,可通过电路设计来增大导通角,达到提高输入功率因数的目的。
- 相关推荐
- 热点推荐
- 功率因数
-
单相桥式整流电容滤波电路的工作原理是什么2024-03-09 8343
-
单相桥式不控整流在不同负载情况下的波形分析 精选资料推荐2021-07-09 2102
-
单相桥式整流滤波电路的电容滤波电路运行过程解析2020-12-24 31672
-
整流电路的谐波和功率因数的学习课件资料免费下载2020-08-18 1137
-
进行三相桥式整流电路功率因数的PSPICE仿真分析资料说明2019-07-25 2487
-
利用MATLAB对单相桥式全控整流电路建模2017-11-02 3459
-
基于MATLAB的单相全控整流电路功率因数测定_崔士杰2016-11-05 1073
-
[原创]单相桥式整流电容滤波电路2010-09-14 3454
-
单相桥式整流电路滤波器参数对功率因数及谐波的影响2010-05-25 972
-
LC滤波的三相桥式整流电路网侧谐波分析2010-05-04 1622
-
整流电路学习课件2009-09-16 7411
-
单相桥式整流滤波负载的电路2009-07-21 5151
-
单相桥式整流电容滤波电路2008-07-14 28083
-
电阻负载的单相桥式全控整流电路2008-01-16 7555
全部0条评论

快来发表一下你的评论吧 !

